Переменные решатели шага в Simulink

Variable-step solvers варьируется размер шага во время симуляции, уменьшая размер шага, чтобы увеличить точность, когда состояния модели изменяются быстро и увеличивают размер шага, чтобы не делать ненужные шаги, когда состояния модели изменяются медленно. Вычисление размера шага добавляет к вычислительным издержкам на каждом шаге, но может сократить общее количество шагов, и следовательно время симуляции, требуемое обеспечить заданный уровень точности для моделей с быстрым изменением или кусочно-непрерывными состояниями.

Когда вы устанавливаете управление Типом панели настройки Решателя к Variable-step, управление Решателем позволяет вам выбирать один из решателей переменного шага. Как с решателями фиксированного шага, набор решателей переменного шага включает дискретный решатель и набор непрерывных решателей. Однако различающийся решатели фиксированного шага, размер шага варьируется динамически на основе локальной ошибки.

Выбор между двумя типами решателей переменного шага зависит от того, ли блоки в ваших состояниях модели define и, если так, тип состояний, которые они задают. Если ваша модель не задает состояний или задает только дискретные состояния, выберите дискретный решатель. Если модель имеет непрерывные состояния, непрерывные решатели используют численное интегрирование, чтобы вычислить значения непрерывных состояний на следующем временном шаге.

Примечание

Если модель не имеет никаких состояний или только дискретных состояний, Simulink^® использует дискретный решатель, чтобы симулировать модель, даже если вы задаете непрерывный решатель.

Переменный шаг дискретный решатель

Используйте переменный шаг дискретный решатель, когда ваша модель не будет содержать непрерывные состояния. Для таких моделей переменный шаг дискретный решатель уменьшает свой размер шага для того, чтобы получить события модели, такие как нулевые пересечения и увеличивает размер шага, когда возможно улучшать производительность симуляции.

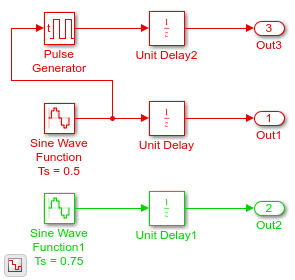
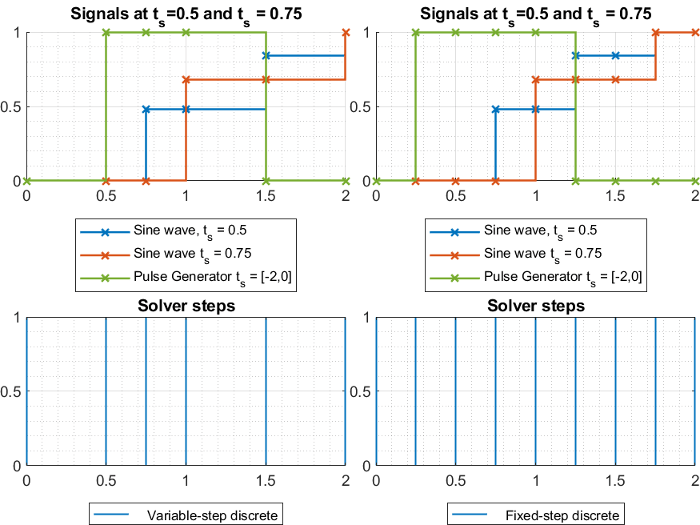
Показанная на рисунке модель содержит два дискретных синусоидальных сигнала в 0,5 и 0,75 шагах расчета. Графики ниже показа сигналы в модели наряду с решателем продвигаются для дискретного переменного шага и фиксированного шага дискретные решатели соответственно. Вы видите, что решатель переменного шага только предпринимает шаги, должен был записать выходной сигнал каждого блока. С другой стороны, решатель фиксированного шага должен будет симулировать с размером фиксированного шага — или основной шаг расчета — 0,25, чтобы записать все сигналы, таким образом делая больше шагов в целом.

Непрерывные решатели с переменным шагом

Решатели переменного шага динамически варьируются размер шага во время симуляции. Каждый из этих решателей увеличивает или уменьшает размер шага с помощью своего локального контроля ошибок, чтобы достигнуть допусков, которые вы задаете. Вычисление размера шага на каждом временном шаге добавляет к вычислительным издержкам. Однако это может сократить общее количество шагов и время симуляции, требуемое обеспечить заданный уровень точности.

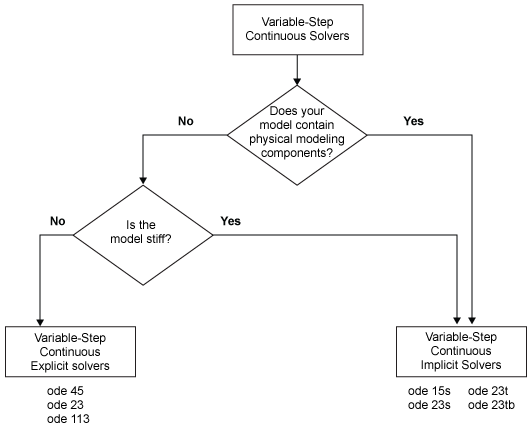
Можно далее категоризировать непрерывные решатели с переменным шагом как один шаг или многоступенчатый, одноразрядный или переменный порядок, и явный или неявный. Смотрите Один Шаг По сравнению с Многоступенчатыми Непрерывными Решателями для получения дополнительной информации.

Переменный шаг непрерывные явные решатели

Переменный шаг явные решатели спроектирован для нежестких проблем. Simulink обеспечивает четыре таких решателя:

ode45
ode23
ode113
odeN

Решатель ОДУ	Метод с одним шагом	Многоступенчатый метод	Порядок точности	Метод
`ode45`	X		Средняя	Рунге-Кутта, Dormand-принц (4,5) пара
`ode23`	X		Низко	Рунге-Кутта (2,3) пара Bogacki & Shampine
`ode113`		X	Переменная, низко к высоко	Реализация PECE Адамса-Бэшфорта-Маултона
`odeN`	X		Смотрите порядок точности на Фиксированном Шаге непрерывные явные решатели	Смотрите метод интегрирования на Фиксированном Шаге непрерывные явные решатели

Решатель ОДУ	Когда использовать
ode45	В общем случае `ode45` решатель является лучшим, чтобы применяться как первая попытка большинства проблем. Рунге-Кутта (4,5) решатель является методом пятого порядка, который выполняет оценку четвертого порядка ошибки. Этот решатель также использует четвертый порядок interpolant, который допускает местоположение события и более сглаженные графики. Если `ode45` является в вычислительном отношении медленным, проблема может быть жесткой и таким образом потребовать неявного решателя.
ode113	Для проблем со строгими ошибочными допусками или для в вычислительном отношении интенсивных проблем, решатель Адамса-Бэшфорта-Маултона PECE может быть более эффективным, чем `ode45`.
ode23	`ode23` может быть более эффективным, чем `ode45` решатель в допусках грубой ошибки и в присутствии умеренной жесткости. Этот решатель предоставляет точные решения путем применения кубической интерполяции Эрмита к значениям и наклонам, вычисленным в концах шага.
odeN	`odeN` решатель использует неадаптивное интегрирование Рунге-Кутта, порядок которого определяется параметром Solver order. `odeN` использует фиксированный размер шага, определенный параметром Max step size, но размер шага может уменьшаться, чтобы получить определенные события решателя, такие как нулевые пересечения и дискретные демонстрационные хиты.

Примечание

Выберите odeN решатель, когда скорость симуляции важна, например, когда

Модель содержит много сброса решателя и/или нулевых пересечений
Solver Profiler не обнаруживает не пройдено шагов при профилировании модели

Переменный шаг непрерывные неявные решатели

Если ваша проблема жестка, попытайтесь использовать один из переменного шага неявные решатели:

ode15s
ode23s
ode23t
ode23tb

Решатель ОДУ	Метод с одним шагом	Многоступенчатый метод	Порядок точности	Метод сброса решателя	'MaxOrder'	Метод
`ode15s`		X	Переменный, низкий и средний	X	X	Числовые формулы дифференцирования (NDFs)
`ode23s`	X		Низко			Модифицированная формула Розенброка второго порядка
`ode23t`	X		Низко	X		Метод трапеций с помощью interpolant
`ode23tb`	X		Низко	X		TR-BDF2

Метод сброса решателя

Для ode15sode23t, и ode23tb выпадающее меню для Solver reset method появляется в разделе Solver details панели Настройки. Этот параметр управляет, как решатель обрабатывает вызванный сброс, например, обнаружением пересечения нулем. Позволенными опциями является Fast и Robust. Fast указывает, что решатель не повторно вычисляет якобиан для сброса решателя, тогда как Robust указывает, что решатель делает. Следовательно, Fast установка в вычислительном отношении быстрее, но она может использовать размер небольшого шага в определенных случаях. Чтобы протестировать на такие случаи, запустите симуляцию с каждой установкой и сравните результаты. Если нет никакого различия в результатах, можно безопасно использовать Fast установка и экономит время. Если результаты значительно отличаются, попытайтесь уменьшать размер шага для быстрой симуляции.

Максимальный порядок

Для ode15s решатель, можно выбрать максимальный порядок числовых формул дифференцирования (NDFs), который применяет решатель. Начиная с ode15s использование сначала - через формулы пятого порядка, Maximum order параметр позволяет вам выбирать порядки 1 - 5. Для жесткой проблемы можно хотеть запуститься с порядка 2.

Советы для выбора Переменного Шага неявный решатель

Следующая таблица обеспечивает советы для приложения переменного шага неявные решатели. Для примера, сравнивающего поведение этих решателей, смотрите, что Решатели Переменного Шага Исследования Используют Жесткую Модель.

Решатель ОДУ	Советы на том, когда использовать
ode15s	`ode15s` решатель переменного порядка на основе числовых формул дифференцирования (NDFs). NDFs связаны с, но более эффективны, чем формулы дифференцирования назад (BDF), которые также известны как метод Гира. `ode15s` решатель численно генерирует якобиевские матрицы. Если вы подозреваете, что проблема жестка, или если `ode45` отказавший или было очень неэффективно, попробуйте `ode15s`. Как правило, запустите путем ограничения максимального порядка NDFs к 2.
ode23s	`ode23s` основан на модифицированной формуле Розенброка порядка 2. Поскольку это - решатель с одним шагом, это может быть более эффективно, чем `ode15s` в грубых допусках. Как `ode15sode23s` численно генерирует якобиевскую матрицу для вас. Однако это может решить определенные виды жестких проблем для который `ode15s` не является эффективным.
ode23t	`ode23t` решатель является реализацией метода трапеций с помощью “свободного” interpolant. Используйте этот решатель, если ваша модель только умеренно жестка, и вам нужно решение без числового затухания. (Энергия не рассеивается, когда вы моделируете колебательное движение.)
ode23tb	`ode23tb` реализация TR-BDF2, неявной формулы Рунге-Кутта с двумя этапами. Первая стадия является шагом метода трапеций, в то время как второй этап использует формулу дифференцирования назад порядка 2. Конструкцией метод использует ту же матрицу итерации в оценке обоих этапов. Как `ode23s`, этот решатель может быть более эффективным, чем `ode15s` в грубых допусках.

Примечание

Для жесткой проблемы решения могут измениться на масштабе времени, который очень мал по сравнению с интервалом интегрирования, в то время как решение интереса изменяется на намного более длительном масштабе времени. Методы, которые не спроектированы для жестких проблем, неэффективны на интервалах, где решение медленно изменяется, потому что эти методы используют временные шаги, достаточно маленькие, чтобы разрешить самое быстрое изменение. Для получения дополнительной информации смотрите Шемпина, L. F. Числовое Решение Ordinary Differential Equations, Chapman & Hall, 1994.

Ошибочные допуски к решателям Переменного Шага

Локальная ошибка

Решатели переменного шага используют стандартные методы управления, чтобы контролировать локальную ошибку на каждом временном шаге. Во время каждого временного шага решатели вычисляют значения состояния в конце шага и определяют локальную ошибку — предполагаемая ошибка этих значений состояния. Они затем сравнивают локальную ошибку с приемлемой ошибкой, которая является функцией и относительной погрешности (rtol) и абсолютной погрешности (атолл). Если локальная ошибка больше приемлемой ошибки для какого-либо состояния, решатель уменьшает размер шага и попробовал еще раз.

Relative tolerance измеряет ошибку относительно размера каждого состояния. Относительная погрешность представляет процент значения состояния. Значение по умолчанию, 1e-3, означает, что вычисленное состояние точно в пределах 0,1%.
Absolute tolerance является пороговым ошибочным значением. Этот допуск представляет приемлемую ошибку как значение измеренного нуля подходов состояния.
Решатели требуют ошибки для iсостояние th, _ei, чтобы удовлетворить:

$e_{i} \leq \max (r t o l \times | x_{i} |, a t o l_{i}) .$

Следующий рисунок показывает график состояния и областей, в которых относительная погрешность и абсолютная погрешность определяют приемлемую ошибку.

Абсолютные погрешности

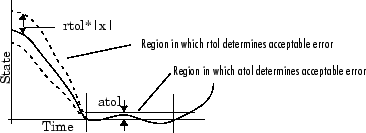
Ваша модель имеет глобальную абсолютную погрешность, которую можно установить на панели Решателя диалогового окна Configuration Parameters. Этот допуск применяется ко всем состояниям в модели. Можно задать auto или действительный скаляр. Если вы задаете auto (значение по умолчанию), Simulink первоначально устанавливает абсолютную погрешность для каждого состояния на основе относительной погрешности. Если относительная погрешность является большим 1e-3, abstol инициализируется в 1e-6. Однако для reltol меньший, чем 1e-3, abstol поскольку состояние инициализируется в reltol * 1e-3. В то время как симуляция прогрессирует, абсолютная погрешность для каждого состояния сброс к максимальному значению, которое состояние приняло до сих пор, времена относительная погрешность для того состояния. Таким образом, если изменения состояния от 0 до 1 и reltol 1e-3, abstol инициализирует в 1e-6, и к концу симуляции достигает 1e-3 также. Если состояние идет от 0 до 1 000, то abstol изменения в 1.

Теперь, если изменения состояния от 0 до 1 и reltol установлен в 1e-4, затем abstol инициализирует в 1e-7, и к концу симуляции достигает значения 1e-4.

Если вычисленное начальное значение для абсолютной погрешности не подходит, можно определить соответствующее значение сами. Вам придется запустить симуляцию несколько раз, чтобы определить соответствующее значение для абсолютной погрешности. Можно также задать, должна ли абсолютная погрешность адаптироваться так же к ее auto установка путем включения или отключения AutoScaleAbsTol параметр. Для получения дополнительной информации смотрите Автоматическую абсолютную погрешность шкалы.

Несколько блоков позволяют вам указывать, что значения абсолютной погрешности для решения модели утверждают, что они вычисляют или которые определяют их выход:

Значения абсолютной погрешности, которые вы задаете для этих блоков, заменяют глобальные настройки в диалоговом окне Configuration Parameters. Вы можете хотеть заменить глобальную установку, если, например, глобальная установка не обеспечивает достаточный контроль ошибок для всех ваших состояний модели, потому что они значительно различаются в величине. Можно установить абсолютную погрешность блока:

auto
–1 (тот же as auto)
positive scalar
real vector (наличие размерности равняется количеству соответствующих непрерывных состояний в блоке),

Советы

Если вы действительно принимаете решение установить абсолютную погрешность, иметь в виду, что слишком низко значения заставляет решатель делать слишком много шагов около значений почти нулевого состояния. В результате симуляция медленнее.

С другой стороны, если вы устанавливаете абсолютную погрешность слишком высоко, ваши результаты могут быть неточными как одно или несколько непрерывных состояний в вашем нуле подхода модели.

Если симуляция завершена, можно проверить точность результатов путем сокращения абсолютной погрешности и выполнения симуляции снова. Если результаты этих двух симуляций удовлетворительно близки, то можно чувствовать себя уверенно в их точности.

Документация