Этот раздел берет вас через функции 2D дискретного стационарного анализа вейвлета с помощью программного обеспечения Wavelet Toolbox™.
| FunctionName | Цель |
|---|---|
Разложение |
| FunctionName | Цель |
|---|---|
Реконструкция |
Стационарная структура разложения вейвлета более послушна, чем вейвлет один. Так, утилиты, полезные для случая вейвлета, не необходимы для Стационарного преобразования вейвлета (SWT).
В этом разделе вы будете учиться
Загрузите изображение
Анализируйте изображение
Выполните одноуровневые и многоуровневые разложения изображений и реконструкции (только командная строка)
denoise изображение
В этом примере мы покажем, как можно использовать 2D стационарный анализ вейвлета для denoise изображение.
Примечание
Вместо того, чтобы использовать image(I) визуализировать изображение I, мы use image(wcodemat(I)), который отображает перемасштабированную версию I продвижение к более ясному представлению деталей и приближениям (см. wcodemat страница с описанием).
Этот пример включает изображение, содержащее шум.
Загрузите изображение.
Из MATLAB® подсказка, ввести
load noiswom whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 96x96 | 73728 | double array |
map | 255x3 | 6120 | double array |
Для SWT, если разложение на уровне k необходим, 2^k должен разделиться равномерно на size(X,1) и size(X,2). Если ваше оригинальное изображение не имеет правильного размера, можно использовать функцию wextend расширять его.
Выполните одноуровневое Стационарное Разложение Вейвлета.
Выполните одноуровневое разложение изображения с помощью db1 вейвлет. Ввод
[swa,swh,swv,swd] = swt2(X,1,'db1');
Это генерирует содействующие матрицы уровня одно приближение (swa) и горизонталь, вертикальные и диагональные детали (swh, swv, и swd, соответственно). Оба имеют размер размера изображения. Ввод
whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 96x96 | 73728 | double array |
map | 255x3 | 6120 | double array |
swa | 96x96 | 73728 | double array |
swh | 96x96 | 73728 | double array |
swv | 96x96 | 73728 | double array |
swd | 96x96 | 73728 | double array |
Отобразите коэффициенты приближения и деталей.
Чтобы отобразить коэффициенты приближения и деталей на уровне 1, ввести
map = pink(size(map,1)); colormap(map)
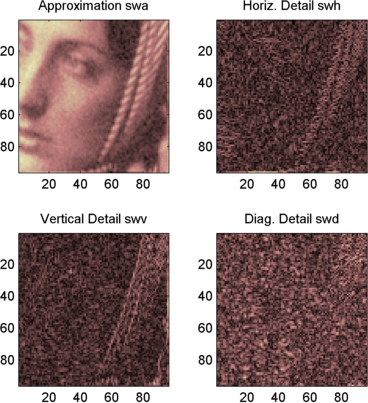
subplot(2,2,1), image(wcodemat(swa,192));
title('Approximation swa')
subplot(2,2,2), image(wcodemat(swh,192));
title('Horiz. Detail swh')
subplot(2,2,3), image(wcodemat(swv,192));
title('Vertical Detail swv')
subplot(2,2,4), image(wcodemat(swd,192));
title('Diag. Detail swd');
Регенерируйте изображение Обратным Стационарным Преобразованием Вейвлета.
Чтобы найти обратное преобразование, ввести
A0 = iswt2(swa,swh,swv,swd,'db1');
Чтобы проверять совершенную реконструкцию, ввести
err = max(max(abs(X-A0)))
err =
1.1369e-13
Создайте и отобразите приближение и детали от коэффициентов.
Создать приближение уровня 1 и детали (A1, H1, V1 и D1) от коэффициентов swa, swh, swv и swdВвод
nulcfs = zeros(size(swa)); A1 = iswt2(swa,nulcfs,nulcfs,nulcfs,'db1'); H1 = iswt2(nulcfs,swh,nulcfs,nulcfs,'db1'); V1 = iswt2(nulcfs,nulcfs,swv,nulcfs,'db1'); D1 = iswt2(nulcfs,nulcfs,nulcfs,swd,'db1');
Чтобы отобразить приближение и детали на уровне 1, ввести
colormap(map)
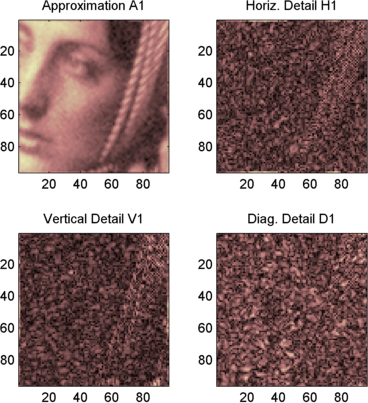
subplot(2,2,1), image(wcodemat(A1,192));
title('Approximation A1')
subplot(2,2,2), image(wcodemat(H1,192));
title('Horiz. Detail H1')
subplot(2,2,3), image(wcodemat(V1,192));
title('Vertical Detail V1')
subplot(2,2,4), image(wcodemat(D1,192));
title('Diag. Detail D1')
Выполните многоуровневое Стационарное Разложение Вейвлета.
Выполнять разложение на уровне 3 изображения (снова использующий db1 вейвлет), ввести
[swa,swh,swv,swd] = swt2(X,3,'db1');
Это генерирует коэффициенты приближений на уровнях 1, 2, и 3 (swa) и коэффициенты деталей (swh, swv и swd). Заметьте что матрицы swa(:,:,i), swh(:,:,i), swv(:,:,i), и swd(:,:,i) для данного уровня i имеют размер размера изображения. Ввод
clear A0 A1 D1 H1 V1 err nulcfs whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 96x96 | 73728 | double array |
map | 255x3 | 6120 | double array |
swa | 96x96x3 | 221184 | double array |
swh | 96x96x3 | 221184 | double array |
swv | 96x96x3 | 221184 | double array |
swd | 96x96x3 | 221184 | double array |
Отобразите коэффициенты приближений и деталей.
Чтобы отобразить коэффициенты приближений и деталей, ввести
colormap(map)
kp = 0;
for i = 1:3
subplot(3,4,kp+1), image(wcodemat(swa(:,:,i),192));
title(['Approx. cfs level ',num2str(i)])
subplot(3,4,kp+2), image(wcodemat(swh(:,:,i),192));
title(['Horiz. Det. cfs level ',num2str(i)])
subplot(3,4,kp+3), image(wcodemat(swv(:,:,i),192));
title(['Vert. Det. cfs level ',num2str(i)])
subplot(3,4,kp+4), image(wcodemat(swd(:,:,i),192));
title(['Diag. Det. cfs level ',num2str(i)])
kp = kp + 4;
end
Восстановите приближение на Уровне 3 и деталях от коэффициентов.
Чтобы восстановить приближение на уровне 3, ввести
mzero = zeros(size(swd)); A = mzero; A(:,:,3) = iswt2(swa,mzero,mzero,mzero,'db1');
Чтобы восстановить детали на уровнях 1, 2 и 3, ввести
H = mzero; V = mzero;
D = mzero;
for i = 1:3
swcfs = mzero; swcfs(:,:,i) = swh(:,:,i);
H(:,:,i) = iswt2(mzero,swcfs,mzero,mzero,'db1');
swcfs = mzero; swcfs(:,:,i) = swv(:,:,i);
V(:,:,i) = iswt2(mzero,mzero,swcfs,mzero,'db1');
swcfs = mzero; swcfs(:,:,i) = swd(:,:,i);
D(:,:,i) = iswt2(mzero,mzero,mzero,swcfs,'db1');
end
Восстановите и отобразите приближения на Уровнях 1, 2 от приближения на Уровне 3 и деталей на Уровнях 1, 2, и 3.
Чтобы восстановить приближения на уровнях 2 и 3, ввести
A(:,:,2) = A(:,:,3) + H(:,:,3) + V(:,:,3) + D(:,:,3); A(:,:,1) = A(:,:,2) + H(:,:,2) + V(:,:,2) + D(:,:,2);
Отобразить приближения и детали на уровнях 1, 2, и 3, тип
colormap(map)
kp = 0;
for i = 1:3
subplot(3,4,kp+1), image(wcodemat(A(:,:,i),192));
title(['Approx. level ',num2str(i)])
subplot(3,4,kp+2), image(wcodemat(H(:,:,i),192));
title(['Horiz. Det. level ',num2str(i)])
subplot(3,4,kp+3), image(wcodemat(V(:,:,i),192));
title(['Vert. Det. level ',num2str(i)])
subplot(3,4,kp+4), image(wcodemat(D(:,:,i),192));
title(['Diag. Det. level ',num2str(i)])
kp = kp + 4;
end
Удалите шум пороговой обработкой.
К denoise изображение используйте пороговое значение, мы находим использование инструмента приложения Wavelet Analyzer (см. следующий раздел), используйте wthresh команда, чтобы выполнить фактическую пороговую обработку коэффициентов детали, и затем использовать iswt2 команда, чтобы получить изображение denoised.
thr = 44.5; sorh = 's'; dswh = wthresh(swh,sorh,thr); dswv = wthresh(swv,sorh,thr); dswd = wthresh(swd,sorh,thr); clean = iswt2(swa,dswh,dswv,dswd,'db1');
Чтобы отобразить и оригинал и изображения denoised, ввести
colormap(map)
subplot(1,2,1), image(wcodemat(X,192));
title('Original image')
subplot(1,2,2), image(wcodemat(clean,192));
title('denoised image')

Второй синтаксис может использоваться для swt2 и iswt2 функции, давая те же результаты:
lev= 4; swc = swt2(X,lev,'db1'); swcden = swc; swcden(:,:,1:end-1) = wthresh(swcden(:,:,1:end-1),sorh,thr); clean = iswt2(swcden,'db1');
Вы получаете тот же график при помощи команд plot на шаге 9 выше.
В этом разделе мы исследуем стратегию изображений шумоподавления на основе 2D стационарного анализа вейвлета с помощью приложения Wavelet Analyzer. Основная идея состоит в том, чтобы составить в среднем много немного отличающихся дискретных исследований вейвлета.
Запустите стационарный вейвлет преобразовывают шумоподавление 2D инструмент.
От подсказки MATLAB ввести waveletAnalyzer.
Wavelet Analyzer появляется:
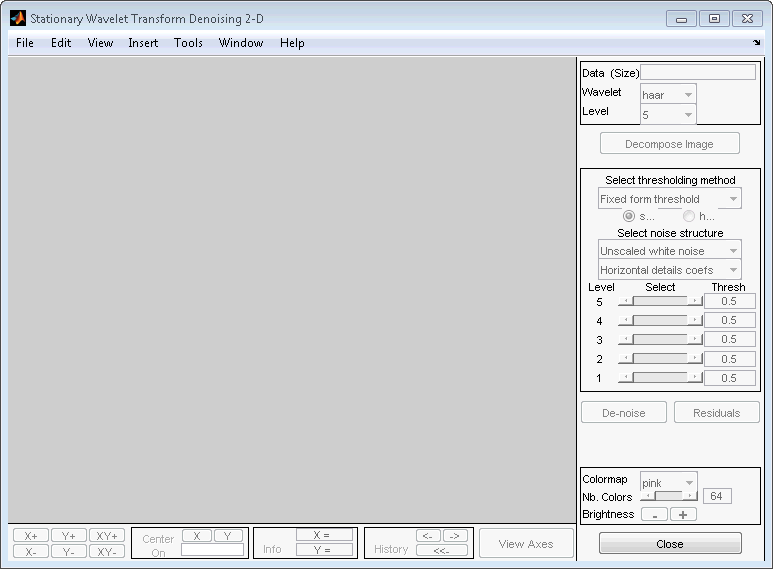
Кликните по пункту меню SWT Denoising 2-D.
Загрузка данных.
В командной строке MATLAB ввести
load noiswom
X переменная. Нажмите ОК, чтобы импортировать изображение.Выполните стационарное разложение вейвлета.
Выберите haar вейвлет в меню Wavelet, выберите 4 из меню Level, и затем нажмите Decompose Image button.
Инструмент отображает гистограммы стационарных коэффициентов детали вейвлета изображения слева от окна. Эти гистограммы организованы можно следующим образом:
От нижней части для уровня 1 к верхней части для уровня 4
На левых горизонтальных коэффициентах, в средних диагональных коэффициентах, и на правильных вертикальных коэффициентах
Denoise изображение с помощью Стационарного Преобразования Вейвлета.
В то время как много опций доступны для подстройки алгоритма шумоподавления, мы примем значения по умолчанию фиксированной формы мягкая пороговая обработка и немасштабированный белый шум. Ползунки, расположенные справа от окна, управляют зависимыми порогами уровня, обозначенными пунктирными линиями, запускающимися вертикально через гистограммы коэффициентов слева от окна. Нажмите кнопку Denoise.
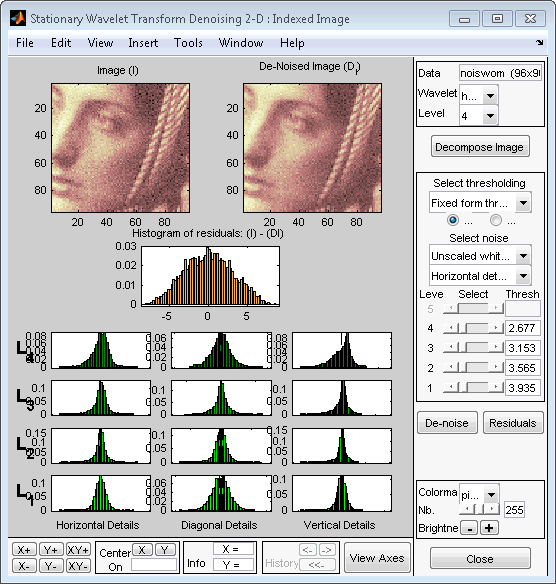
Результат, кажется, сверхсглаживается и выбранные слишком агрессивные пороги. Тем не менее, гистограмма остаточных значений довольно хороша, поскольку это близко к Распределению Гаусса, которое является шумом, введенным, чтобы произвести анализируемое изображение noiswom.mat от части оригинального изображения woman.mat.
Выбор метода задания порога.
В Избранном меню метода задания порога выберите Penalize низкий элемент. Связанное значение по умолчанию для режима пороговой обработки автоматически установлено в трудно; примите его. Используйте ползунок Разреженности, чтобы настроить пороговое значение близко к 45,5, и затем нажать denoise кнопку.
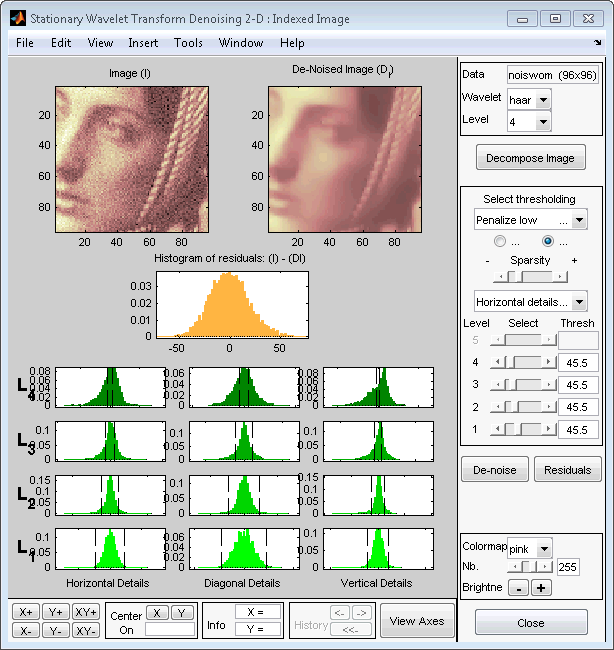
Результат является довольно удовлетворительным, несмотря на то, что возможно улучшить его немного.
Выберите sym6 вейвлет и нажимает Decompose Image button. Используйте ползунок Разреженности, чтобы настроить пороговое значение близко к 40,44, и затем нажать denoise кнопку.
Инструмент позволяет вам сохранить изображение denoised на диск. Тулбокс создает MAT-файл в текущей папке с именем, которое вы выбираете.
Чтобы сохранить denoised образ от существующего процесса шумоподавления, используйте файл меню>, Сохраняют denoised Образ. Диалоговое окно появляется, который позволяет вам задать папку и имя файла для хранения изображения. Введите имя dnoiswom. После сохранения данных изображения к файлу dnoiswom.mat, загрузите переменные в свою рабочую область:
load dnoiswom whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 96x96 | 73728 | double array |
map | 255x3 | 6120 | double array |
valTHR | 3x4 | 96 | double array |
wname | 1x4 | 8 | char array |
Изображением denoised является X и map палитра. Кроме того, параметры процесса шумоподавления доступны. Имя вейвлета содержится в wname, и зависимые пороги уровня закодированы в valTHR. Переменная valTHR имеет четыре столбца (уровень разложения) и три строки (один для каждой ориентации детали).