Модулируйте однополосную амплитудную модуляцию использования
Аналоговая модуляция полосы пропускания, в модуляции
Блок SSB AM Modulator Passband модулирует однополосную амплитудную модуляцию использования с фильтром преобразования Гильберта. Выход является представлением полосы пропускания модулируемого сигнала. Оба сигналы ввода и вывода являются действительными скалярными сигналами.
Полоса пропускания Модулятора SSB AM передает или более низкий или верхний сигнал боковой полосы, но не обоих. Чтобы управлять, какую боковую полосу это передает, используйте параметр Sideband to modulate.
Если входом является u (t) в зависимости от времени t, то выход
где:
f c является параметром Carrier frequency.
θ параметр Initial phase.
û (t) является преобразованием Гильберта входа u (t).
Знак "минус" указывает на верхнюю боковую полосу, и знак "плюс" указывает на более низкую боковую полосу.
Этот блок использует блок Analytic Signal из библиотеки блоков Преобразований DSP System Toolbox™.
Блок Analytic Signal вычисляет комплексный аналитический сигнал, соответствующий каждому каналу действительного входа M на n, u
где и обозначает преобразование Гильберта. Действительная часть выхода в каждом канале является копией действительного входа в том канале; мнимая часть является преобразованием Гильберта входа. В частотном диапазоне аналитический сигнал сохраняет положительное содержимое частоты исходного сигнала при обнулении отрицательных частот и удвоении компонента DC.
Блок вычисляет преобразование Гильберта с помощью equiripple КИХ-фильтра с порядком, заданным параметром Порядка фильтра, n. Линейный фильтр фазы создан с использованием алгоритм обмена Remez и налагает задержку n/2 на входных выборках.
Для лучших результатов используйте несущую частоту, которая, как оценивается, больше, чем 10% частоты дискретизации вашего входного сигнала. Это происходит из-за реализации преобразования Гильберта посредством фильтра.
В следующем примере мы производим входной сигнал на 10 Гц на 8 000 выборок в секунду. Мы затем определяем фильтр преобразования Гильберта порядка 100. Ниже ответ фильтра преобразования Гильберта, как возвращено fvtool.
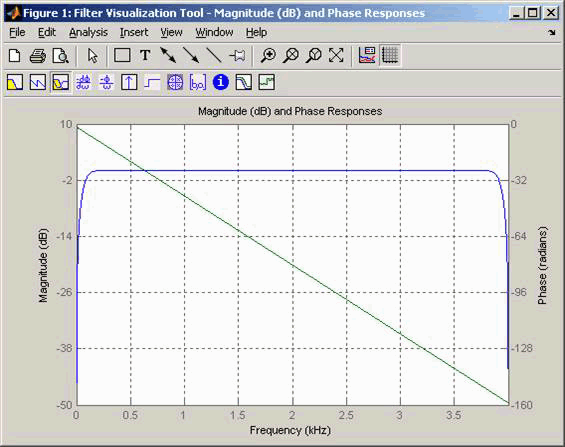
Отметьте полосу пропускания ответа величины фильтра. Путем выбора несущей частоты, больше, чем 10% (но меньше чем 90%) шага расчета входного сигнала (8 000 выборок в секунду, в этом примере) или эквивалентно, несущая частота, больше, чем 400 Гц, мы гарантируем, что Фильтр преобразования Гильберта будет действовать в плоском разделе ответа величины фильтра (отображенный синим), и что наш модулируемый сигнал будет иметь желаемую величину и форму.
Как правило, соответствующее значение Carrier frequency намного выше, чем самая высокая частота входного сигнала. Теоремой отсчетов Найквиста обратная величина шага расчета модели (заданный источником модели сигнала) должна превысить дважды параметр Carrier frequency.
Это кладка блоков только с действительными входными параметрами типа double. Этот блок не работает в триггируемой подсистеме.
Частота несущей.
Смещение фазы, , из модулируемого сигнала.
Этот параметр задает, передать ли верхнюю или более низкую боковую полосу.
Длина КИХ-фильтра использовалась для расчета преобразования Гильберта.
[1] Пиблс, принципы системы связи Пейтона З младшего. Чтение, масса.: Аддисон-Уэсли, 1976.