Скалярное квантование является процессом, который сопоставляет все входные параметры в заданной области к общему значению. Это карты процессов вводит в различной области значений значений к различному общему значению. В действительности скалярное квантование оцифровывает аналоговый сигнал. Два параметра определяют квантование: раздел и книга шифров.
Раздел квантования задает несколько непрерывных, неперекрывающихся областей значений значений в наборе вещественных чисел. Задавать раздел в MATLAB® среда, перечислите отличные конечные точки различных областей значений в векторе.
Например, если раздел разделяет линию вещественного числа на четыре набора
X: x ≤ 0}
X: 0 <x ≤ 1}
X: 1 <x ≤ 3}
X: 3 <x}
затем можно представлять раздел как трехэлементный вектор
partition = [0,1,3];
Длина вектора раздела является той меньше, чем количество интервалов раздела.
Книга шифров говорит квантизатор, какое общее значение присвоить входным параметрам, которые попадают в каждую область значений раздела. Представляйте книгу шифров как вектор, длина которого совпадает с количеством интервалов раздела. Например, вектор
codebook = [-1, 0.5, 2, 3];
одна возможная книга шифров для раздела [0,1,3].
quantiz функционируйте также возвращает вектор, который говорит, в каком интервале каждый вход находится. Например, выход ниже говорит, что входные записи лежат в интервалах, помеченных 0, 6, и 5, соответственно. Здесь, 0th интервал состоит из вещественных чисел, меньше чем или равных 3; 6-й интервал состоит из вещественных чисел, больше, чем 8, но меньше чем или равный 9; и 5-й интервал состоит из вещественных чисел, больше, чем 7, но меньше чем или равный 8.
partition = [3,4,5,6,7,8,9]; index = quantiz([2 9 8],partition)
Выход
index =
0
6
5
Если вы продолжаете этот пример путем определения вектора книги шифров такой как
codebook = [3,3,4,5,6,7,8,9];
затем уравнение ниже связывает векторный index к квантованному quants сигнала.
quants = codebook(index+1);
Эта формула для quants точно что quantiz функционируйте использование, если вы вместо этого формулируете пример более кратко как ниже.
partition = [3,4,5,6,7,8,9]; codebook = [3,3,4,5,6,7,8,9]; [index,quants] = quantiz([2 9 8],partition,codebook);
Квантование искажает сигнал. Можно уменьшать искажение путем выбора соответствующего раздела и параметров книги шифров. Однако тестирование и выбор параметров для больших наборов сигнала с прекрасной схемой квантования могут быть утомительными. Один способ произвести раздел и параметры книги шифров легко состоит в том, чтобы оптимизировать их согласно набору так называемых обучающих данных.
Примечание
Обучающие данные, которые вы используете, должны быть типичны для видов сигналов, которые вы будете на самом деле квантовать.
lloyds функция оптимизирует раздел и книгу шифров согласно алгоритму Ллойда. Код ниже оптимизирует раздел и книгу шифров в течение одного периода синусоидального сигнала, начинающего с грубого исходного предположения. Затем это использует эти параметры, чтобы квантовать исходный сигнал с помощью параметров исходного предположения, а также оптимизированных параметров. Выход показывает, что среднеквадратическое искажение после квантования намного меньше для оптимизированных параметров. quantiz функция автоматически вычисляет среднеквадратическое искажение и возвращает его как третий выходной параметр.
% Start with the setup from 2nd example in "Quantizing a Signal." t = [0:.1:2*pi]; sig = sin(t); partition = [-1:.2:1]; codebook = [-1.2:.2:1]; % Now optimize, using codebook as an initial guess. [partition2,codebook2] = lloyds(sig,codebook); [index,quants,distor] = quantiz(sig,partition,codebook); [index2,quant2,distor2] = quantiz(sig,partition2,codebook2); % Compare mean square distortions from initial and optimized [distor, distor2] % parameters.
Выход
ans =
0.0148 0.0024Код ниже показов, как quantiz функционируйте использует partition и codebook сопоставлять вектор действительных чисел, samp, к новому вектору, quantized, чьи записи или-1, 0.5, 2, или 3.
partition = [0,1,3]; codebook = [-1, 0.5, 2, 3]; samp = [-2.4, -1, -.2, 0, .2, 1, 1.2, 1.9, 2, 2.9, 3, 3.5, 5]; [index,quantized] = quantiz(samp,partition,codebook); quantized
Выход ниже.
quantized =
Columns 1 through 6
-1.0000 -1.0000 -1.0000 -1.0000 0.5000 0.5000
Columns 7 through 12
2.0000 2.0000 2.0000 2.0000 2.0000 3.0000
Column 13
3.0000
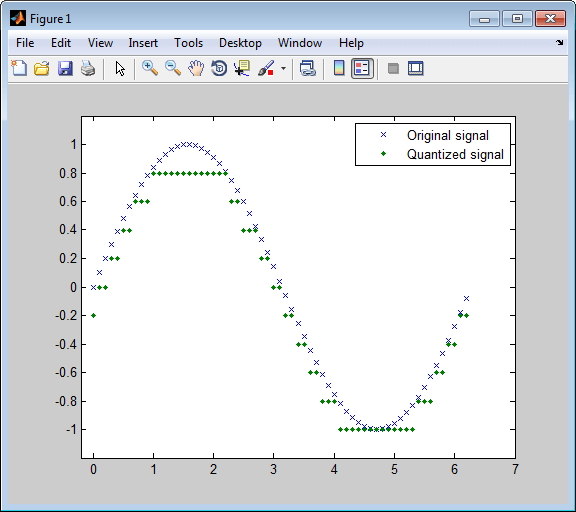
Этот пример иллюстрирует природу скалярного квантования более ясно. После квантования произведенной синусоиды это строит исходные и квантованные сигналы. График контрастирует xэто составляет синусоиду с точками, которые составляют квантованный сигнал. Вертикальная координата каждой точки является значением в векторном codebook.
t = [0:.1:2*pi]; % Times at which to sample the sine function sig = sin(t); % Original signal, a sine wave partition = [-1:.2:1]; % Length 11, to represent 12 intervals codebook = [-1.2:.2:1]; % Length 12, one entry for each interval [index,quants] = quantiz(sig,partition,codebook); % Quantize. plot(t,sig,'x',t,quants,'.') legend('Original signal','Quantized signal'); axis([-.2 7 -1.2 1.2])