Определите коэффициенты прямых линейных предикторов N-го порядка
DSP System Toolbox / Оценка / Линейное предсказание
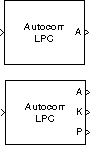
Блок Autocorrelation LPC решает, что коэффициенты N-шага передают линейный предиктор для timeseries в каждом входном канале длины-M, u, путем минимизации ошибки предсказания в смысле наименьших квадратов. Линейный предиктор является КИХ-фильтром, который предсказывает следующее значение в последовательности от настоящих и прошлых входных параметров. Этот метод имеет приложения в создании фильтра, речевом кодировании, спектральном анализе и системе идентификации.
Блок Autocorrelation LPC может вывести ошибку предсказания для каждого канала как полиномиальные коэффициенты, отражательные коэффициенты или оба. Блок может также вывести ошибочную степень предсказания для каждого канала.
Типы данных |
|
Прямое сквозное соединение |
|
Многомерные сигналы |
|
Сигналы переменного размера |
|
Обнаружение пересечения нулем |
|
Блок Autocorrelation LPC вычисляет решение методом наименьших квадратов к
где указывает на 2-норму и
Решение задачи наименьших квадратов через нормальные уравнения
приводит к системе уравнений
где r = [r1 r2 r3... rn+1]T оценка автокорреляции для u, вычисленного с помощью блока Autocorrelation, и * указывает на комплексное сопряженное транспонирование. Нормальные уравнения решены в O (n2) операции блоком Левинсона-Дербина.
Обратите внимание на то, что решение проблемы LPC очень тесно связано с методом Уокера Рождества АРА спектральной оценки. В том контексте нормальные уравнения выше упоминаются как уравнения Уокера Рождества АРА.
[1] Haykin, S. Адаптивная Теория Фильтра. 3-й редактор Englewood Cliffs, NJ: Prentice Hall, 1996.
[2] Ljung, L. System Identification: теория для пользователя. Englewood Cliffs, NJ: Prentice Hall, 1987. PGS. 278-280.
[3] Proakis, J. и Д. Мэнолакис. Цифровая обработка сигналов. 3-й редактор Englewood Cliffs, NJ: Prentice Hall, 1996.