Используйте эффективный оборудованием алгоритм, чтобы решить системы линейных уравнений с комплексным знаком

Открыть скрипт

В этом примере показано, как решить системы линейных уравнений с комплексным знаком с помощью эффективного оборудованием кода MATLAB® в Simulink® с помощью систолического массива.

Обзор

Этот пример показывает аппаратный эффективный метод решения системы одновременных уравнений

$$AX = B$$

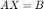
где A является матрицей комплекса m на n, X матрица комплекса n-by-p, и B является матрицей комплекса m-by-p.

Модель Simulink, используемая в этом примере:

model = 'fi_complex_mldivide_systolic_array_model';
open(model)

Активированные подсистемы, которые отправляют данные, содержат блоки MATLAB function, которые отслеживают, которого входа отправить затем, и отправляют строки матриц A и B, чтобы блокироваться "4x4, Комплексная Левая Матрица CORDIC Делится" когда ready сигнал высок. Если вы отправляете данные когда ready высоко, вы не будете уже делать недействительным данных в трубопроводе.

Алгоритм перезаписывает матрицу А с верхней треугольной матрицей R. Алгоритм перезаписывает B с C = Q'B, где Q унитарен и QR = A. Алгоритм использует заднюю замену относительно уравнения верхней треугольной матрицы

$$RX = C.$$

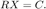
Чтобы исследовать алгоритм, посмотрите Под маской блока "4x4, Комплексная Левая Матрица CORDIC Делится".

Задайте параметры

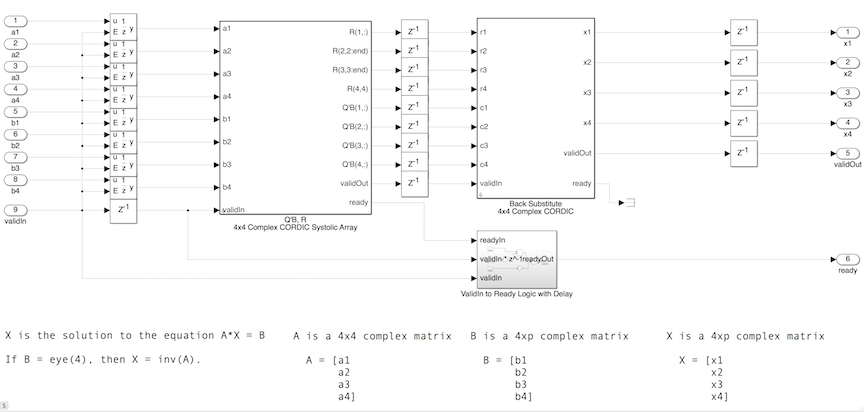
Задайте комплексные матрицы A и B в базовом рабочем пространстве. В этом примере матрица А должна быть 4 на 4, и матрица B должна быть 4 p, где p является количеством правых сторон.

rng('default');
A = complex(randn(4,4),randn(4,4));
B = complex(randn(4,1),randn(4,1));

Метод использует алгоритм CORDIC, таким образом, необходимо также задать количество итераций ядра CORDIC в NumberOfCORDICIterations параметр, или на параметрах блоков "4x4 Комплексная Левая Матрица CORDIC Делят" блок.

Когда A и B будут двойная точность типы данных с плавающей точкой, определите номер итераций CORDIC к количеству битов в мантиссе двойного. Если входные параметры являются фиксированной точкой, то количество итераций CORDIC должно быть меньше размера слова. Точность расчета улучшается на один бит для каждой итерации до размера слова входных параметров. Эта модель будет работать с фиксированной точкой и одним типами данных.

NumberOfCORDICIterations = 52;

Необходимо также инстанцировать переменной BackSubstitutePrototype чтобы задать тип данных, используемый в задней замене или ввести прототипное значение в параметры блоков "4x4 Комплексная Левая Матрица CORDIC, Делят" блок. В этом случае матрицы A и B являются двойными, таким образом, устанавливает BackSubstitutePrototype значение, чтобы быть двойным. Эта переменная используется функцией броска, чтобы бросить переменные задней замены с помощью 'подобного' синтаксиса.

BackSubstitutePrototype = 0;

Запустите модель

Выключите ожидаемые предупреждения прежде, чем запустить модель.

warning_state = warning('off','Coder:builtins:ConstantFoldingOverFlow');
sim(model)

После симуляции модель возвращает матрицу X, которая является решением матричного уравнения

$$AX = B$$

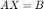
Проверьте результаты путем проверки, что AX-B является маленьким значением.

err = norm(A*X - B)

err =

   6.5270e-15

QR-алгоритм

Алгоритм CORDIC используется для расчета, разложение QR как в примерах Выполняет QR-факторизацию Используя CORDIC и Реализацию Эффективное Оборудованием Разложение QR Используя CORDIC в Систолическом Массиве.

Этот пример имеет матрицу А 4 на 4. Можно разместить блоки рядом в этой модели, чтобы создать до любой матрицы размера.

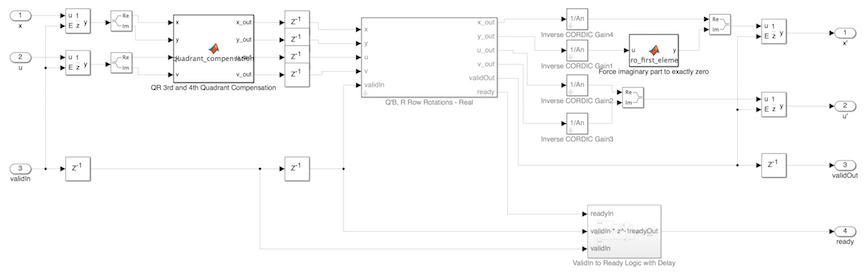
Чтобы видеть QR-алгоритм, посмотрите под маской для блока "Q'B, R 4x4 Complex CORDIC Systolic Array".

Комплексный QR

Поскольку данные в этом примере являются комплексными, дополнительный шаг требуется, чтобы обнулять мнимые части центров, чтобы сделать их с действительным знаком. Это сделано путем разделения данных в действительные и мнимые части и использования CORDIC, чтобы обнулить мнимую часть, как будто это были две строки действительной матрицы. Это эквивалентно комплексному умножению

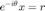
$e^{-i\theta} x = r$

где

$
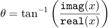
\theta = \tan^{-1}\left({\mbox{\texttt{imag}}(x)\over \mbox{\texttt{real}}(x)}\right)
$

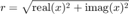
$r = \sqrt{\mbox{real}(x)^2 + \mbox{imag}(x)^2}$

за исключением того, что расчет сделан с помощью алгоритма CORDIC без квадратов или квадратных корней.

Чтобы видеть алгоритм для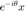 $e^{-i\theta} x$ , посмотрите под маской для блока "Rotate first element to real".

Обратная замена

Наконец, чтобы вычислить X, вычислите обратные величины диагональных элементов R и задней замены в правую сторону C. Использование алгоритма CORDIC делит реализацию, чтобы вычислить обратные величины.

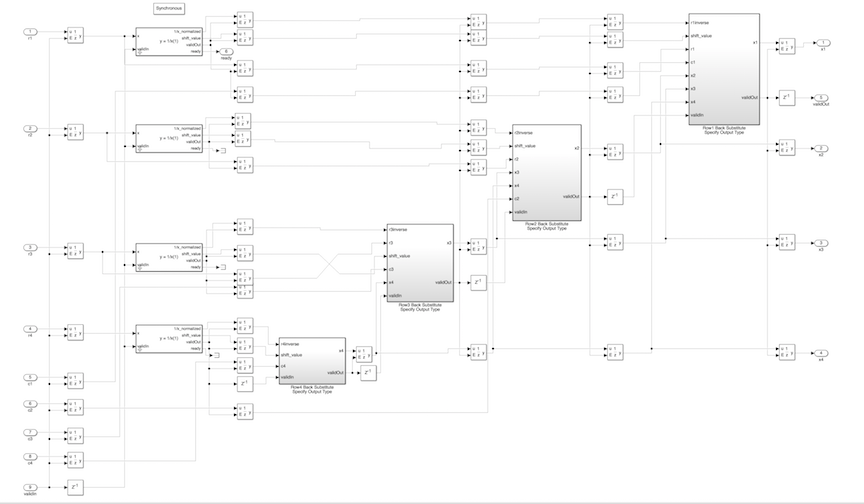
Чтобы видеть алгоритм задней замены, посмотрите под маской для блока "Back Substitute 4x4 Complex CORDIC".

Обращение матриц

Является обычно ненужным явным образом вычислить инверсию матрицы [3], [5]. Однако, если вы хотите для этого набор B равный единичной матрице I. Затем решение уравнения

$$AX = I$$

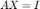
равняется

$X = A^{-1}.$

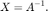
A = complex(2*rand(4,4)-1,2*rand(4,4)-1);
B = complex(eye(4));
NumberOfCORDICIterations = 52;
BackSubstitutePrototype = 0;

Симулируйте модель

sim(model)

Проверьте, что AX и XA близко к единичной матрице. Будут небольшие различия из-за ошибок округления.

A*X

ans =

   1.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -0.0000 - 0.0000i
   0.0000 - 0.0000i   1.0000 + 0.0000i  -0.0000 + 0.0000i  -0.0000 + 0.0000i
  -0.0000 + 0.0000i   0.0000 - 0.0000i   1.0000 + 0.0000i   0.0000 + 0.0000i
   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i   1.0000 - 0.0000i

X*A

ans =

   1.0000 - 0.0000i  -0.0000 - 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i
   0.0000 + 0.0000i   1.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i
   0.0000 + 0.0000i   0.0000 + 0.0000i   1.0000 - 0.0000i  -0.0000 + 0.0000i
   0.0000 - 0.0000i  -0.0000 - 0.0000i  -0.0000 + 0.0000i   1.0000 + 0.0000i

Дробное масштабирование

Нормализация к дробным типам делает расчеты легче в фиксированной точке. Можно масштабировать матрицы так, чтобы их данные были в области значений [-1, +1], и используйте дробные фиксированные точки потому что решение матричного уравнения

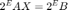
$$2^E AX = 2^EB$$

совпадает с решением

$$AX = B.$$

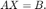
Чтобы преобразовать в дробное масштабирование без дополнительной стоимости в сгенерированном коде, можно использовать функцию reinterpretcast в MATLAB или блок Data Type Conversion в Simulink с "Вводом и выводом, чтобы иметь равное Сохраненное Целое число".

Запустите исчерпывающие тестовые точки

Можно запустить много тестовых воздействий через модель путем создания A и 3D массивы B.

m = 4;
n = 4;
p = 1;
n_test_inputs=100;

Создайте входные параметры, таким образом, что действительные и мнимые части находятся в области значений [-1, +1]

A = complex(2*rand(m,n,n_test_inputs)-1, 2*rand(m,n,n_test_inputs)-1);
B = complex(2*rand(m,p,n_test_inputs)-1, 2*rand(m,p,n_test_inputs)-1);

В этом примере матрицы A и B уже содержали действительные и мнимые части в области значений [-1, +1], таким образом, устанавливает типы быть дробными.

data_word_length = 24;
data_fraction_length = 23;

Типы данных QR

Рост в элементах R в действительной QR-факторизации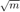 $\sqrt{m}$ (см., Выполняют QR-факторизацию Используя CORDIC). Элементы являются комплексными в этом примере, таким образом, дополнительный фактор роста 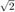$\sqrt{2}$ необходим потому что

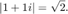
$|1+1i| = \sqrt{2}.$

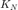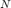Кроме того, алгоритм CORDIC выращивает промежуточные значения следующим фактором усиления $K_N$ , где $N$ количество итераций CORDIC, прежде чем это будет нормировано.

$
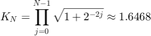
K_N = \prod_{j=0}^{N-1}{\sqrt{1+2^{-2j}}} \approx 1.6468
$

Поэтому upperbound для роста в QR-алгоритме для матрицы А комплекса m на n является продуктом всех факторов роста:

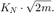
$K_N \cdot \sqrt{2m}.$

Это этот пример, A 4 на 4, таким образом, максимальный фактор роста в QR-алгоритме

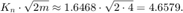
$K_n \cdot \sqrt{2m} \approx 1.6468 \cdot \sqrt{2\cdot 4} = 4.6579.$

Поэтому количество дополнительных целочисленных битов, чтобы позволить в QR-алгоритме избегать переполнения, когда у вас есть m=4 строки:

qr_growth_bits = ceil(log2(1.6468*sqrt(2*m)))

qr_growth_bits =

     3

Бросьте матрицы A и B к фиксированной точке

Модель требует, чтобы входные параметры были подписаны и размер слова B совпасть с размером слова A.

Вырастите данные wordlength, чтобы вместить рост QR.

qr_input_word_length = data_word_length + qr_growth_bits

qr_input_word_length =

    27

Бросьте к фиксированной точке и B к типу А.

T.A = fi([], 1, qr_input_word_length, data_fraction_length);
T.B = T.A;

A = cast(A, 'like', T.A);
B = cast(B, 'like', T.B);

Тип данных Обратной замены

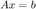Если $A$ $n$ $n$ обратимой комплексной матрицей и $x$ решение матричного уравнения $Ax=b$ , то с помощью свойств векторных и матричных норм (см., например, ссылку [6]), этому можно показать это

$
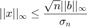
||x||_\infty \leq \frac{\sqrt{n}||b||_\infty}{\sigma_n}
$

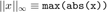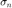где $||x||_\infty \equiv \mbox{\texttt{max(abs(x))}}$ и $\sigma_n$ самое маленькое сингулярное значение $A$ . Связанный связан с числом обусловленности $A$ .

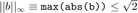В этом примере, $b$ комплексный вектор с действительными и мнимыми частями, ограниченными 1. Поэтому $||b||_\infty \equiv \mbox{\texttt{max(abs(b))}}\leq \sqrt{2}$ .

Поэтому, если вы знаете распределение сингулярных значений для $A$ матриц в вашей проблеме, затем можно выбрать количество дополнительных целочисленных битов, требуемых избегать переполнения в задней замене с данной вероятностью (см., например, ссылку [1]).

В этом примере мы вычисляем сингулярные значения для всех матриц в нашем испытательном стенде и выбираем количество целочисленных битов, чтобы избежать переполнения на основе этого.

singular_values = zeros(n,n_test_inputs);
A0 = double(A);
for k = 1:n_test_inputs
    singular_values(:,k) = svd(A0(:,:,k));
end
condition_numbers = singular_values(1,:)./singular_values(end,:);
x_bound = sqrt(2*n)./singular_values(end,:);

Количество битов роста, чтобы добавить является основой 2 логарифма связанного максимума.

integer_bits_for_backsubstitute = ceil(log2(max(x_bound)))

integer_bits_for_backsubstitute =

     7

Вычтите необходимые целочисленные биты для задней замены от wordlength и дополнительный бит для знакового бита.

backsubstitute_fraction_length = T.A.WordLength - integer_bits_for_backsubstitute - 1

backsubstitute_fraction_length =

    19

Поэтому тип данных для задней замены:

BackSubstitutePrototype = fi(0, 1, T.A.WordLength, backsubstitute_fraction_length)

BackSubstitutePrototype = 

     0

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 27
        FractionLength: 19

Определите номер итераций CORDIC, чтобы быть тем меньше, чем размер слова фиксированной точки A.

NumberOfCORDICIterations = T.A.WordLength - 1

NumberOfCORDICIterations =

    26

Запустите модель с входными параметрами фиксированной точки.

sim(model)

Вычислите и постройте ошибки

Мера ошибки

norm(AX - B)

для каждой пары входных параметров A и B.

norm_error = zeros(1,size(X,3));
B0 = double(B);
X0 = double(X);
for k = 1:size(X,3)
    norm_error(k) = norm(A0(:,:,k)*X0(:,:,k) - B0(:,:,k));
end

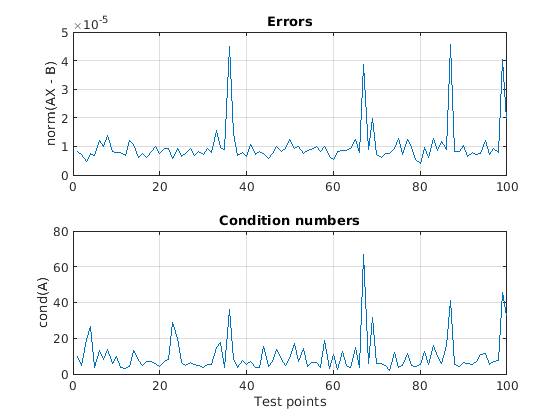
Постройте ошибки. Ошибки являются низкими из-за выбранных типов данных. Ошибки обычно выше, когда число обусловленности матрицы А высоко, как теория предсказывает.

figure(1)
clf
h1 = subplot(2,1,1);
plot(norm_error)
grid on
title('Errors')
ylabel('norm(AX - B)')
h2 = subplot(2,1,2);
plot(condition_numbers)
grid on
title('Condition numbers')
ylabel('cond(A)')
xlabel('Test points')
linkaxes([h1,h2],'x')

Повторно включите предупреждения

warning(warning_state);

Ссылки

[1] Цзычжун Чэнь и Джек Дж. Донгарра. "Числа обусловленности Гауссовых Случайных Матриц". SIAM Journal на Анализе матрицы и Приложения. 27.3 (июль 2005), стр 603-620.

[2] Джордж Э. Форсайт и Клив Б. Молер. Компьютерное решение линейных алгебраических систем. Englewood Cliffs, Нью-Джерси: Prentice Hall, 1967.

[3] Джордж Э. Форсайт, М.А. Молком и Клив Б. Молер. Компьютерные методы для математических вычислений. Englewood Cliffs, Нью-Джерси: Prentice Hall, 1977.

[4] Клив Б. Молер. Угол Клива: Каково Число обусловленности Матрицы?, MathWorks, Inc. 2017.

[5] Клив Б. Молер. Числовое Вычисление с MATLAB. SIAM, 2004. ISBN: 978-0-898716-60-3.

[6] Джин Х. Голуб и ссуда Чарльза Ф. Вана. Матричные расчеты. Johns Hopkins University Press.

%#ok<*NOPTS,*NASGU>

Документация Fixed-Point Designer

Поддержка

Сообщество Экспонента