Можно создать диаграммы нулей и полюсов линейных идентифицированных моделей. Чтобы изучить полюса и нули шумового компонента модели ввода - вывода или модели временных рядов, использовать noise2meas сначала извлекать шумовую модель как независимую модель ввода - вывода, входные параметры которой являются шумовыми каналами исходной модели.
Для примеров создания диаграмм нулей и полюсов смотрите полюса Модели и Нули Используя полюса Приложения и Графика System Identification и Нули в Командной строке.
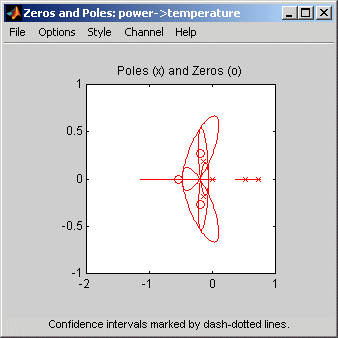
Следующий рисунок показывает демонстрационную диаграмму нулей и полюсов модели с доверительными интервалами. x укажите на полюса и o укажите на нули.
Общим уравнением линейной динамической системы дают:
В этом уравнении G является оператором, который берет вход к выходу и получает системную динамику, и v является аддитивной шумовой частью.
Полюса линейной системы являются корнями знаменателя передаточной функции G. Полюса имеют непосредственное влияние на динамические свойства системы. Нули являются корнями числителя G. Если вы оценили шумовую модель H в дополнение к динамической модели G, можно также просмотреть полюса и нули шумовой модели.
Нули и полюса являются эквивалентными способами описать коэффициенты линейного разностного уравнения, такие как модель ARX. Полюса сопоставлены с выходной стороной разностного уравнения, и нули сопоставлены с входной стороной уравнения. Количество полюсов равно количеству интервалов выборки между наиболее задержанным и наименее задержанным выходом. Количество нулей равно количеству интервалов выборки между наиболее задержанным и наименее задержанным входом. Например, там два полюса и один нуль в следующей модели ARX:
Можно отобразить доверительный интервал для каждого полюса и нуля на графике. Чтобы изучить, как показать или скрыть доверительный интервал, смотрите полюса Модели и Нули Используя полюса Приложения и Графика System Identification и Нули в Командной строке.
Доверительный интервал соответствует области значений полюса или нулевых значений с определенной вероятностью того, чтобы быть фактическим полюсом или нулем системы. Тулбокс использует оцененную неопределенность в параметрах модели, чтобы вычислить доверительные интервалы и принимает, что оценки имеют Распределение Гаусса.
Например, для 95%-го доверительного интервала, область вокруг номинального полюса или нулевого значения представляет область значений значений, которые имеют 95%-ю вероятность того, чтобы быть истинным системным полюсом или нулевым значением. Можно задать доверительный интервал как вероятность (между 0 и 1) или как количество стандартных отклонений Распределения Гаусса. Например, вероятность 0,99 (99%) соответствует 2,58 стандартным отклонениям.
Можно использовать диаграммы нулей и полюсов, чтобы оценить, может ли быть полезно уменьшать порядок модели. Когда доверительные интервалы для нулевого полюсом парного перекрытия, это перекрытие указывает на возможное удаление нулей-полюсов. Для получения дополнительной информации смотрите Уменьшающий Порядок Модели Использовать Диаграммы нулей и полюсов.