Документация

Разворачивание сферы к плоскости

Картографы разработали сотни проекций карты, более чем несколько тысяч лет. Три больших семьи проекции карты, плюс несколько меньших единиц, обычно подтверждаются. Они основаны на типах геометрических фигур, которые используются, чтобы передать функции от сферы или сфероида к плоскости. Проекции карты основаны на разрабатываемых поверхностях, и три традиционных семейства состоят из цилиндров, конусов и плоскостей. Они используются, чтобы классифицировать большинство проекций, включая некоторых, которые аналитически (геометрически) не создаются. Кроме того, много проекций карты основаны на многогранниках. В то время как многогранные проекции имеют интересные и полезные свойства, они не описаны в этом руководстве.

Какая разрабатываемая поверхность использовать для проекции зависит от того, какая область должна быть сопоставлена, ее географическая степень и геометрические свойства, которые области, контуры, и направляют потребность иметь, учитывая цель карты. Следующие разделы описывают и иллюстрируют, как цилиндрические, конические, и азимутальные семейства проекций карты создаются, и обеспечивает некоторые примеры проекций, которые основаны на них.

Цилиндрические проекции

Цилиндрическая проекция производится путем переноса цилиндра вокруг земного шара, представляющего Землю. Проекция карты является изображением земного шара, спроектированного на цилиндрическую поверхность, которая затем развернута в плоскую поверхность. Когда цилиндр выравнивается с полярной осью, параллели появляются как горизонтальные линии и меридианы как вертикальные линии. Цилиндрические проекции могут быть или равной областью, конформной, или равноотстоящей. Следующий рисунок показывает регулярную цилиндрическую или нормальную ориентацию аспекта, в которой цилиндр является касательной к Земле вдоль Экватора, и проекция исходит горизонтально от оси вращения. Метод проекции схематически изображается слева, и пример дан справа (равная область цилиндрическая проекция, нормальный/экваториальный аспект).

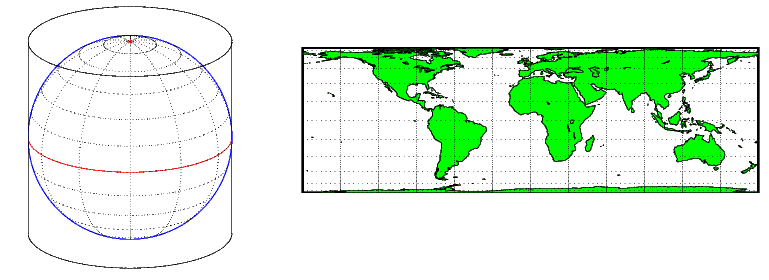
Для описания аспекта проекции смотрите Аспект Проекции.

Некоторые широко используемые цилиндрические проекции карты

Конические проекции

Коническая проекция выведена из проекции земного шара на конус, помещенный по нему. Для нормального аспекта вершина конуса находится на полярной оси Земли. Если конус касается Земли во всего одной конкретной параллели, это называется касательной. Если сделано меньший, конус пересечет Землю дважды, в этом случае это называется секансом. Конические проекции часто достигают меньшего количества искажения в середине - и высокие широты, чем цилиндрические проекции. Дальнейшая разработка является поликонической проекцией, которая развертывает семейство касательной или секущих конусов, чтобы заключить в скобки последовательность полос параллелей, чтобы дать еще к меньшему количеству искажения шкалы. Следующая фигура иллюстрирует коническую проекцию, схематически изображая ее конструкцию слева, с примером справа (проекция равной области Алберса, полярный аспект).

Некоторые широко используемые конические проекции

Азимутальные проекции

Азимутальная проекция является проекцией земного шара на плоскость. В полярном аспекте азимутальная проекция сопоставляет с плоской касательной к Земле в одном из полюсов, с меридианами, спроектированными как прямые линии, исходящие от полюса, и параллельна показавший полными кругами, сосредоточенными в полюсе. Азимутальные проекции (особенно ортогональное) могут иметь экваториальные или наклонные аспекты. Проекция сосредоточена на точке, которая является или на поверхности, в центре Земли, в антиподе, некотором расстоянии вне Земли, или в бесконечности. Большинство азимутальных проекций не подходит для отображения целой Земли в одном представлении, но дает смысл земного шара. Следующая фигура иллюстрирует азимутальную проекцию, схематически изображая его слева, с примером справа (ортогональная проекция, полярный аспект).

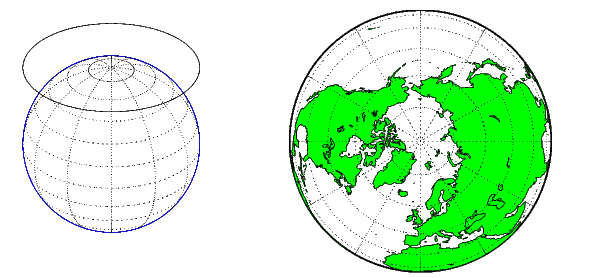
Некоторые широко используемые азимутальные проекции