Можно применять преобразование Cox Поля любому этапному или функция ответа узел модели (любые модели с глобальным значком) путем выбора Model> Set Up и введения номера для lambda в окне редактирования Box-Cox.
Для Гауссовых моделей процессов (GPMs) и линейных моделей (полиномы, полиномиальные сплайны и RBFs) можно также использовать диалоговое окно Box-Cox Transformation, описанное в следующем разделе, при помощи кнопки на панели инструментов или пункта меню Model Box-Cox Transform.
Вы можете хотеть преобразовать функцию ответа любой, чтобы откорректировать для ненормальности и/или heteroscedastic структуры отклонения. Полезный класс преобразований с этой целью является степенью, преобразовывают
, где λ является параметром, который будет определен. Поле и Cox (1964) показали, как λ и сами коэффициенты регрессии могли быть оценены одновременно с помощью метода наибольшего правдоподобия. Процедура состоит из проведения стандартного использования метода наименьших квадратов
для 
λ
для 
где так называемым геометрическим средним значением наблюдений дают
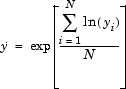
Оценка наибольшего правдоподобия λ соответствует значению, для которого SSE (λ) от подобранной модели является минимумом. Это значение λ определяется путем подбирания модели (принятый повсюду, чтобы быть заданным матрицей регрессии для полной модели - X) для различных уровней λ и выбора значения, соответствующего минимальному SSE (λ). График SSE (λ) по сравнению с λ часто используется, чтобы упростить этот выбор.
Параметр λ развертывается между областью значений-3 к 3 с шагом 0,5.
Можно ввести значение для lambda в окне редактирования, которое приближается к точке на графике с самым маленьким SSE.
Несмотря на то, что SSE (λ) является непрерывной функцией λ, простой выбор для λ рекомендуется. Это вызвано тем, что практическое различие между 0,5 и 0.593, скажем, вероятно, будет очень мало, но простое преобразование как 0,5 намного легче интерпретировать.
Можно также найти аппроксимированное 100 
(1-) доверительный интервал на l путем вычисления
где количество остаточных степеней свободы, равных (N-q).
В этой формуле λ, как изучают, является значением, которое минимизирует SSE (λ). Обратите внимание на то, что этот доверительный интервал может охватить больше чем одно инкрементное значение для λ. В этом случае любое из этих значений так же допустимо как любой другой, и можно выбрать любое из этих преобразований, из которых можно разработать испытательные модели.
Необходимо всегда смотреть на графики остаточных значений наверху, чтобы видеть эффект различных преобразований.
Можно создать несколько дочерних вершин одной модели и выбрать различные преобразования для каждого, чтобы сравнить их использующий остальную часть инструментов Model Browser.
Ради ясности рассмотрите следующий пример, который иллюстрирует результаты применения алгоритма Cox Поля к модели крутящего момента полисплайна.
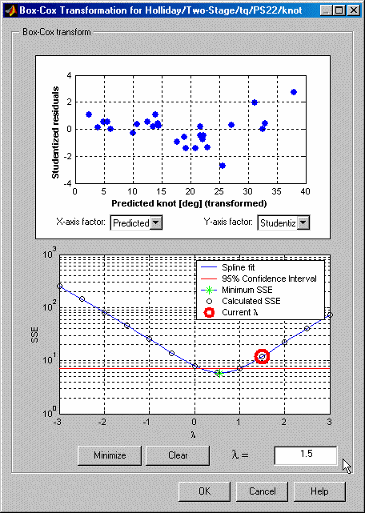
В этом примере минимальное значение SSE (λ) происходит близко к λ = 0. Минимум отмечен зеленым. 95%-й предел достоверности был вычислен и продвинут фигура как красная сплошная линия. Очевидно в этом примере, что, после округления к самому близкому инкрементному значению, содержавшему в доверительном интервале, любой λ в области значений
является соответствующим. Из трех возможного шага, 0, 0.5, и 1, λ = 0.5 является самым близким к минимальному SSE.
Можно выбрать любую точку на графике путем нажатия. Выбранная точка (текущий lambda) затем обрисована в общих чертах в красном. Можно также ввести значения lambda непосредственно в окне редактирования и нажать Enter.
