Документация

Сглаженные формулировки несглаженных функций

Чтобы сглаживать в противном случае несглаженную проблему, можно иногда добавлять вспомогательные переменные. Например,

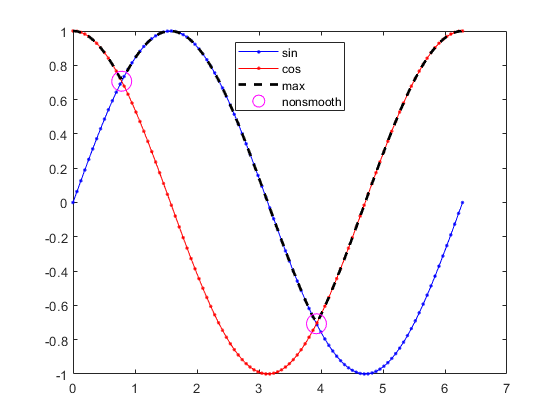
может быть несглаженная функция, даже когда g (x) и h (x) является гладким, как проиллюстрировано следующими функциями.

f (x) несглажен в точках x = π/4 и x = 5π/4.

 Код для создания фигуры

x = linspace(0,2*pi);
g = @sin;
h = @cos;
f = @(x)max(g(x),h(x));
plot(x,g(x),'b.-',x,h(x),'r.-')
hold on
plot(x,f(x),'k--',"LineWidth",2)
t = [pi,5*pi]/4;
plot(t,sin(t),'mo',"MarkerSize",15)
legend("sin","cos","max","nonsmooth","Location","north")
hold off

Это отсутствие гладкости может вызвать проблемы для решателей Optimization Toolbox™, все из которых принимают, что целевые функции и нелинейные ограничительные функции непрерывно дифференцируемы. Так, при попытке решить

x = min_t (f (t)) начинающий с точки x0 = 1,

вы не получаете выходной флаг 1, потому что решение не дифференцируемо в локально минимизирующей точке x = π/4.

fun1 = @sin;
fun2 = @cos;
fun = @(x)max(fun1(x),fun2(x));
[x1,fval1,eflag1] = fminunc(fun,1)

Local minimum possible.

fminunc stopped because it cannot decrease the objective function
along the current search direction.

<stopping criteria details>

x1 =

    0.7854


fval1 =

    0.7071


eflag1 =

     5

Иногда, можно использовать вспомогательную переменную, чтобы превратить несглаженную проблему в сглаженную проблему. Для предыдущего примера рассмотрите вспомогательную переменную y со сглаженными ограничениями

Рассмотрите задачу оптимизации согласно этим ограничениям,

Получившееся решение xY решение исходной проблемы

Эта формулировка использует подход, основанный на проблеме.

myvar = optimvar("myvar");
auxvar = optimvar("auxvar");
smprob = optimproblem("Objective",auxvar);
smprob.Constraints.cons1 = auxvar >= sin(myvar);
smprob.Constraints.cons2 = auxvar >= cos(myvar);
x0.myvar = 1;
x0.auxvar = 1;
[sol2,fval2,eflag2] = solve(smprob,x0)

Solving problem using fmincon.

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

sol2 = 

  struct with fields:

    auxvar: 0.7071
     myvar: 0.7854


fval2 =

    0.7071


eflag2 = 

    OptimalSolution

Эта та же концепция лежит в основе формулировки fminimax функция; см. Целевой Метод Достижения.

Смотрите также

fgoalattain | fminimax

Похожие темы

• Целевой метод достижения