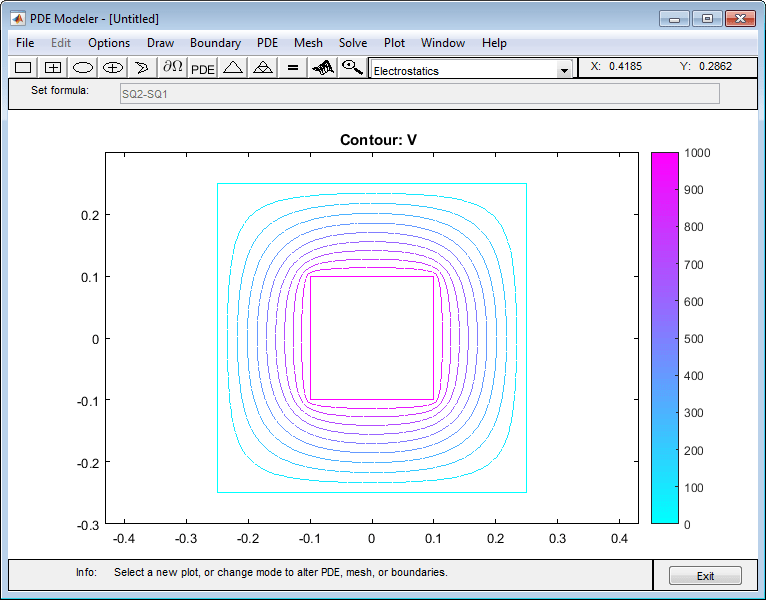
Найдите электростатический потенциал в заполненной воздухом кольцевой четырехсторонней системе координат с помощью приложения PDE Modeler. В данном примере используйте следующие параметры:
Внутренняя квадратная сторона составляет 0,2 м
Внешняя квадратная сторона составляет 0,5 м
Электростатический потенциал во внутренней границе 1000V
Электростатический потенциал во внешней границе является 0V
УЧП, управляющий этой проблемой, является уравнением Poisson
– ∇ · (ε ∇V) = ρ.
Приложение PDE Modeler использует относительную проницаемость ε r = ε/ε0, где ε 0 является абсолютной диэлектрической проницаемостью вакуума (8.854 · 10-12 фарада/метр). Относительная проницаемость для воздуха 1.00059. Обратите внимание на то, что коэффициент проницаемости не влияет на результат в этом примере, пока коэффициент является постоянным.
Предположение, что существует бесплатно в области, можно упростить уравнение Poisson до уравнения Лапласа,
ΔV = 0.
Здесь, граничные условия являются граничными условиями Дирихле V = 1000 во внутренней границе и V = 0 во внешней границе.
Чтобы решить эту задачу в приложении PDE Modeler, выполните эти шаги:
Чертите следующие два квадрата.
pderect([-0.1 0.1 -0.1 0.1]) pderect([-0.25 0.25 -0.25 0.25])
Установите и x - и y - пределы по осям [-0.3 0.3]. Для этого выберите Options> Axes Limits и установите соответствующие области значений. Затем выберите Options> Axes Equal.
Смоделируйте систему координат путем ввода SQ2-SQ1 в поле Set formula.
Установите режим приложения на Electrostatics.
Задайте граничные условия. Для этого переключитесь на граничный режим путем выбора Boundary> Boundary Mode. Используйте Shift +click, чтобы выбрать несколько контуров. Затем выберите Boundary> Specify Boundary Conditions.
Для внутренних границ используйте граничное условие Дирихле с h = 1 и r = 1000.
Для внешних границ используйте граничное условие Дирихле с h = 1 и r = 0.
Задайте коэффициенты путем выбора PDE> PDE Specification или нажатия кнопки PDE на панели инструментов. Задайте epsilon = 1 и rho = 0.
Инициализируйте mesh путем выбора Mesh> Initialize Mesh.
Решите УЧП путем выбора Solve> Solve PDE или нажатия кнопки = на панели инструментов.
Постройте эквипотенциальные графики с помощью контурного графика. Для этого выберите Plot> Parameters и выберите контурный график в получившемся диалоговом окне.
Улучшите точность решения путем совершенствования mesh близко к повторно используемым углам, где градиенты круты. Для этого выберите Solve> Parameters. Выберите Adaptive mode, используйте метод выбора Worst triangles и определите максимальный номер треугольников к 500. Выберите Mesh> Refine Mesh.
Решите УЧП с помощью усовершенствованной mesh. Чтобы отобразить эквипотенциальные линии на уровне каждого 100-го вольта, выберите Plot> Parameters и введите 0:100:1000 в поле Contour plot levels.