3-Zone Pipe (2P)

Кабелепровод для транспорта изменяющей фазу жидкости с теплопередачей

Библиотека:
Simscape / Жидкости / Двухфазная Жидкость / Pipes & Fittings

Описание

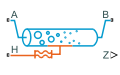
Блок Pipe (2P) моделирует трубопроводы с изменяющей фазу жидкостью. Каждая жидкая фаза называется зоной, которая является дробным значением между 0 и 1. Зоны не смешиваются. Трубопровод С 3 зонами (2P) использует следующую за контуром модель, чтобы отследить подохлажденную жидкость (L), жидкая паром смесь (M), и перегретый пар (V) в трех зонах. Относительная сумма места, которое зона занимает в системе, называется зональной частью длины в системе.

Порт H является тепловым портом, который представляет температуру окружающей среды. Уровень теплопередачи между жидкостью и средой зависит от жидкой фазы каждой зоны. Стена трубопровода моделируется в блоке, и температура трубопровода стенки в каждой зоне может отличаться. Давление и температура под влиянием жидкой динамической сжимаемости и жидкой зональной тепловой способности.

Теплопередача между жидкостью и стеной

Конвективный коэффициент теплопередачи между жидкостью и стеной, _αF, варьируется на зону согласно номеру Nusselt:

$α_{F} = \frac{Nu k}{D_{H}},$

где:

Nu зона номер Nusselt.
k средняя жидкая теплопроводность.
D _H является трубопроводом Hydraulic diameter, эквивалентный диаметр некруглого сечения.

Номер Nusselt, используемый в коэффициенте теплопередачи, является большими из турбулентных - и ламинарное течение цифры Nusselt.

Для турбулентных течений в подохлажденных жидких или перегретых зонах пара номер Nusselt вычисляется с корреляцией Гниелинского:

$Nu = \frac{\frac{f}{8} (Re - 1000) PR}{1 + 12.7 {(\frac{f}{8})}^{1 / 2} ({Pr}_{}^{2 / 3} - 1)},$

где:

Re зональное среднее число Рейнольдса.
Pr зональное среднее число Прандтля.
f является коэффициентом трения Дарси, вычисленным от корреляции Haaland:

$\frac{1}{\sqrt{f_{}}} = - 1.8 журнал [{(\frac{\frac{ε}{D_{H}}}{3.7})}^{1.11} + \frac{6.9}{{Re}_{}}],$
где ε является стеной Internal surface absolute roughness.

Для турбулентных течений в зоне смеси жидкого пара номер Nusselt вычисляется с корреляцией Каваллини-Цеккина:

$Nu = \frac{_{\sl}^{b} {PR}_{\sl}^{c} {{[(\sqrt{\frac{ρ_{SL}}{ρ_{SV}}} - 1) x_{Out} + 1]}^{1 + b} - {[(\sqrt{\frac{ρ_{SL}}{ρ_{SV}}} - 1) x_{In} + 1]}^{1 + b}}}{(1 + b) (\sqrt{\frac{ρ_{SL}}{ρ_{SV}}} - 1) (x_{Out} - x_{In})} .$

Где:

_SL Re является числом Рейнольдса влажной жидкости.
_SL Pr является числом Прандтля влажной жидкости.
_SL ρ является плотностью влажной жидкости.
ρ _SV является плотностью влажного пара.
a = 0.05, b = 0.8, и c = 0.33.

Когда пластины моделируются на внутренней поверхности трубопровода, коэффициент теплопередачи:

$α_{F} = \frac{Nu k}{D_{H}} (1 + η_{Int} s_{Int}),$

где:

_Int η является Internal fin efficiency.
_Int s является Ratio of internal fins surface area to no-fin surface area.

Для ламинарных течений номер Nusselt определяется параметром Laminar flow Nusselt number.

Определенная энтальпия

Уровень теплопередачи от жидкости основан на изменении в определенной энтальпии в каждой зоне:

$Q = {\dot{m}}_{Q} (Δ h_{L} + Δ h_{M} + Δ h_{V}),$

где ${\dot{m}}_{Q}$ массовый расход жидкости для теплопередачи. Это - входной массовый расход жидкости трубопровода, также $\dot{m}$ _A или $\dot{m}$ _B, в зависимости от направления потока жидкости.

В жидкости и зонах пара, изменение в определенной энтальпии задано как:

$Δ h = c_{p} (T_{H} - T_{I}) [1 - exp (- \frac{z S_{W}}{{\dot{m}}_{Q} c_{p} (α_{F}^{- 1} + α_{E}^{- 1})})],$

где:

_cp является удельной теплоемкостью жидкости или пара.
_TH является температурой окружающей среды.
_TI является жидкой входной температурой.
z является жидкой зональной частью длины.
_αE является коэффициентом теплопередачи между стеной и средой.
_SW является стенной площадью поверхности:

$S_{W} = \frac{4 A}{D_{H}} L,$
где:
- A является трубопроводом Cross-sectional area.
- L является Pipe length.
Обратите внимание на то, что эта стенная площадь поверхности не включает финансовую область, которая задана в параметрах Ratio of internal fins surface area to no-fin surface area и Ratio of external fins surface area to no-fin surface area. Пластины установлены пропорционально стенной площади поверхности. Значение 0 средние значения там не являются никакими пластинами на стене трубопровода.

В зоне смеси жидкого пара изменение в определенной энтальпии вычисляется как:

$Δ h = (T_{H} - T_{S}) \frac{z S_{W}}{{\dot{m}}_{Q} (α_{F}^{- 1} + α_{E}^{- 1})},$

где _TS является жидкой температурой насыщения. Это принято, что смесь жидкого пара всегда при этой температуре.

Уровень теплопередачи

Общая теплопередача между жидкостью и стеной трубопровода является суммой теплопередачи в каждой жидкой фазе:

$Q_{F} = Q_{F,L} + Q_{F,V} + Q_{F,M} .$

Уровень теплопередачи между жидкостью и трубопроводом в жидкой зоне:

$Q_{F,L} = {\dot{m}}_{Q} c_{p,L} [T_{W,L} - min (T_{I}, T_{S})] [1 - exp (- \frac{z_{L} S_{W} α_{L}}{{\dot{m}}_{Q} c_{p,L}})] .$

где _TW,L является температурой стены, окружающей жидкую зону.

Уровень теплопередачи между жидкостью и трубопроводом в зоне смеси:

$Q_{F,M} = (T_{H} - T_{Sat}) z_{M} S_{W} α_{M} .$

Уровень теплопередачи между жидкостью и трубопроводом в зоне пара:

$Q_{F,V} = {\dot{m}}_{Q} c_{p,V} [T_{W,V} - min (T_{I}, T_{Sat})] [1 - exp (- \frac{z_{V} S_{W} α_{V}}{{\dot{m}}_{Q} c_{p,V}})],$

где _TW,V является температурой стены, окружающей зону пара.

Теплопередача между стеной и средой

Если стена трубопровода имеет конечную толщину, коэффициент теплопередачи между стеной и средой, _αE, задан:

$\frac{1}{α_{E}} = \frac{1}{α_{W}} + \frac{1}{α_{Ext} (1 + η_{Ext} s_{Ext})},$

где α _W является коэффициентом теплопередачи из-за проводимости через стену:

$α_{W} = \frac{k_{W}}{D_{H} ln (1 + \frac{t_{W}}{D_{H}})},$

и где:

_kW является Wall thermal conductivity.
_tW является Wall thickness.
_{Расширением} α является External environment heat transfer coefficient.
_{Расширением} η является External fin efficiency.
_{Расширением} s является Ratio of external fins surface area to no-fin surface area.

Если стена не имеет количества тепла, коэффициент теплопередачи между стеной и средой равняется коэффициенту теплопередачи среды, _{Расширения} α.

Уровень теплопередачи

Уровень теплопередачи между каждой стенной зоной и средой:

$Q_{H,zone} = (T_{H} - T_{W}) z S_{W} α_{E} .$

Общая теплопередача между стеной и средой:

$Q_{H} = Q_{H,L} + Q_{H,V} + Q_{H,M} .$

Управление дифференциальными уравнениями

Уровень теплопередачи зависит от количества тепла стены, _CW:

$C_{W} = c_{p,W} ρ_{W} S_{W} (t_{W} + \frac{t_{W}^{2}}{D_{H}}),$

где:

c _{p, W} является Wall specific heat.
_ρW является Wall density.

Управляющие уравнения для теплопередачи между жидкостью и внешней средой для жидкой зоны:

$Q_{H,L} - Q_{F,L} = C_{W} [z_{L} \frac{d T_{W,L}}{d t} + max (\frac{d z_{L}}{d t}, 0) (T_{W,L} - T_{W,M})],$

для зоны смеси:

$Q_{H,M} - Q_{F,M} = C_{W} [z_{M} \frac{d T_{W,M}}{d t} + min (\frac{d z_{L}}{d t}, 0) (T_{W,L} - T_{W,M}) + min (\frac{d z_{V}}{d t}, 0) (T_{W,V} - T_{W,M})],$

и для зоны пара:

$Q_{H,V} - Q_{F,V} = C_{W} [z_{V} \frac{d T_{W,V}}{d t} + max (\frac{d z_{V}}{d t}, 0) (T_{W,V} - T_{W,M})] .$

Баланс импульса

Перепад давления по трубопроводу состоит из двух факторов: изменения в давлении из-за изменений в плотности и изменений в давлении из-за трения в стенах трубопровода.

Для турбулентных течений, когда число Рейнольдса выше Turbulent flow lower Reynolds number limit, падение давления вычисляется в терминах коэффициента трения Дарси. Перепад давления между портом A и внутренним узлом я:

$p_{A} - p_{I} = (\frac{1}{ρ_{I}} - \frac{1}{ρ_{A}^{*}}) {(\frac{{\dot{m}}_{A}}{S})}^{2} + \frac{f_{A} {\dot{m}}_{A} | {\dot{m}}_{A} |}{2 ρ_{I} D_{H} S_{}^{2}} (\frac{L + L_{Add}}{2}),$

где:

_ρI является плотностью жидкости во внутреннем узле I.
_ρA* является плотностью жидкости в порте A. Это совпадает с _ρA, когда поток является установившимся; когда поток является переходным, он вычисляется от жидкого внутреннего состояния с адиабатическим выражением:

$u_{A}^{*} + \frac{p_{A}}{ρ_{A}^{*}} + \frac{1}{2} {(\frac{{\dot{m}}_{A}}{ρ_{A}^{*} S})}^{2} = h + \frac{1}{2} {(\frac{{\dot{m}}_{A}}{ρ S})}^{2},$
где:
- h является средней определенной энтальпией, $h = h_{L} z_{L} + h_{V} z_{V} + h_{M} z_{M} .$
- ρ является средней плотностью, $ρ = ρ_{L} z_{L} + ρ_{M} z_{M} + ρ_{V} z_{V} .$
Это - то, вследствие того, что вычисление теплопередачи происходит во внутреннем узле I.
$\dot{m}$ _A является массовым расходом жидкости через порт A.
L является Pipe length.
L _{Добавляет}, Aggregate equivalent length of local resistances, который является эквивалентной длиной трубы, которая вводит то же самое значение потери как сумма потерь из-за других локальных сопротивлений.

Обратите внимание на то, что коэффициент трения Дарси зависит от числа Рейнольдса и вычисляется в обоих портах.

Перепад давления между портом B и внутренним узлом я:

$p_{B} - p_{I} = (\frac{1}{ρ_{I}} - \frac{1}{ρ_{B}^{*}}) {(\frac{{\dot{m}}_{B}}{S})}^{2} + \frac{f_{B} {\dot{m}}_{B} | {\dot{m}}_{B} |}{2 ρ_{I} D_{H} S_{}^{2}} (\frac{L + L_{Add}}{2}) .$

где:

_ρB* является плотностью жидкости в порте B. Это совпадает с _ρB, когда поток является установившимся; когда поток является переходным, он вычисляется от жидкого внутреннего состояния с адиабатическим выражением:

$u_{B}^{*} + \frac{p_{B}}{ρ_{B}^{*}} + \frac{1}{2} {(\frac{{\dot{m}}_{B}}{ρ_{B}^{*} S})}^{2} = h + \frac{1}{2} {(\frac{{\dot{m}}_{B}}{ρ S})}^{2} .$
$\dot{m}$ _B является массовым расходом жидкости через порт B.

Для ламинарных течений, когда число Рейнольдса ниже Laminar flow upper Reynolds number limit, падение давления на трение вычисляется в терминах Laminar friction constant for Darcy friction factor, λ. Перепад давления между портом A и внутренним узлом я:

$p_{A} - p_{I} = (\frac{1}{ρ_{I}} - \frac{1}{ρ_{A}^{*}}) {(\frac{{\dot{m}}_{A}}{S})}^{2} + \frac{λ μ {\dot{m}}_{A}}{2 ρ_{I} D_{H}^{2} S} (\frac{L + L_{Add}}{2}),$

где μ является средней жидкой динамической вязкостью:

$μ = μ_{L} z_{L} + μ_{M} z_{M} + μ_{V} z_{V} .$

Перепад давления между портом B и внутренним узлом я:

$p_{B} - p_{I} = (\frac{1}{ρ_{I}} - \frac{1}{ρ_{B}^{*}}) {(\frac{{\dot{m}}_{B}}{S})}^{2} + \frac{λ μ {\dot{m}}_{B}}{2 ρ_{I} D_{H}^{2} S} (\frac{L + L_{Add}}{2}) .$

Для переходных потоков перепад давления из-за вязкого трения является сглаживавшим смешением между значениями для ламинарного и турбулентного падения давления.

Баланс массы

Общая массовая скорость накопления задана как:

$\frac{d M}{d t} = {\dot{m}}_{A} + {\dot{m}}_{B},$

где M является общей жидкой массой в трубопроводе. В терминах жидких зон массовая скорость накопления является функцией изменения в плотности, ρ, относительно давления, p, и жидкой определенной внутренней энергии, u:

$\frac{d M}{d t} = [{(\frac{d ρ}{d p})}_{u} \frac{d p}{d t} + {(\frac{d ρ}{d u})}_{p} \frac{d u_{o u t}}{d t} + ρ_{L} \frac{d z_{L}}{d t} + ρ_{M} \frac{d z_{M}}{d t} + ρ_{V} \frac{d z_{V}}{d t}] V,$

где:

_uout является определенной внутренней энергией после того, как вся теплопередача произошла.
V является общим объемом жидкости или объемом трубопровода.

Энергетический баланс

Энергетическое уравнение разговора:

$M \frac{d u_{o u t}}{d t} + ({\dot{m}}_{A} + {\dot{m}}_{B}) u_{o u t} = ϕ_{A} + ϕ_{B} + Q_{F},$

где:

ϕ _A является энергетической скоростью потока жидкости в порте A.
ϕ _B является энергетической скоростью потока жидкости в порте B.
Q _F является уровнем теплопередачи между жидкостью и стеной.

Допущения и ограничения

Стена трубопровода совершенно тверда.
Поток полностью разрабатывается. Потери на трение и теплопередача не включают эффекты входа.
Инерция жидкости незначительна.
Эффект силы тяжести незначителен.
Когда давление выше жидкого критического давления, большие значения тепловых свойств жидкости (такие как число Прандтля, теплопроводность и удельная теплоемкость) не могут точно отразить теплообмен в трубопроводе.

Порты

Вывод

развернуть все

`Z` — Зональные части длины
физический сигнал

Вектор с частями длины жидкости, смешанной фазы и зон пара в трубопроводе.

Сохранение

развернуть все

`A` — Открытие трубопровода
двухфазная жидкость

Открытие, через который двухфазные потоки жидкости в или из трубопровода. Порты A и B могут каждый функционировать или как вход или как выход. Тепловая проводимость позволена между двухфазными жидкими портами и жидкостью, внутренней к трубопроводу (хотя его удар обычно релевантен только при почти нулевых скоростях потока жидкости).

`B` — Открытие трубопровода
двухфазная жидкость

`H` — Передайте стену по каналу
тепловой

Тепловое граничное условие в наружной поверхности стены трубопровода. Используйте этот порт, чтобы получить теплообмен различных видов — например, проводящий, конвективный, или радиационный — между стеной трубопровода и средой. Теплообмен между внутренней поверхностью стены и жидкостью получен непосредственно в блоке.

Параметры

развернуть все

Геометрия

`Pipe length` — Расстояние между портами трубопровода
`5 m` (значение по умолчанию) | положительная скалярная величина с единицами длины

Расстояние между портами трубопровода. Жидкое, двухфазное, и зоны пара каждый включает часть этого расстояния. Зональные части могут варьироваться, но их совокупная длина, совпадая с расстоянием трубопровода, фиксируется.

`Cross-sectional area` — Внутренняя область, нормальная к направлению потока
`0.01 m^2` (значение по умолчанию) | положительная скалярная величина с единицами площади

Внутренняя область трубопровода, нормального к направлению потока. Сечение трубопровода принято постоянным в его длине.

`Hydraulic diameter` — Диаметр цилиндрического трубопровода с данной площадью поперечного сечения
`0.1 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

Отношение площади открытия сечения трубопровода к периметру той области. Трубопровод не требуется, чтобы быть цилиндрическим, и его поперечное сечение имеют любую форму. Этот параметр дает диаметр, который имело бы общее сечение, если бы это было круговым.

Вязкое трение

`Aggregate equivalent length of local resistances` — Незначительное падение давления в трубопроводе, описанном как длина
`1 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

Объединенная продолжительность всех локальных сопротивлений, существующих в трубопроводе. Локальные сопротивления включают повороты, подборы кривой, арматуры, и передают по каналу входы и выходы. Эффект локальных сопротивлений состоит в том, чтобы увеличить эффективную длину трубопровода. Эта длина добавляется к геометрической длине трубопровода для вычислений трения.

`Internal surface absolute roughness` — Средняя глубина поверхностных дефектов на внутренней поверхности трубопровода
`15e-6 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

Средняя глубина всей поверхности дезертирует на внутренней поверхности трубопровода. Поверхностные дефекты влияют на падение давления через трубопровод в режиме турбулентного течения.

`Laminar flow upper Reynolds number limit` — Число Рейнольдса, ниже которого поток ламинарен
`2e+3` (значение по умолчанию) | положительный безразмерный скаляр

Число Рейнольдса, выше которого поток трубопровода начинается к переходу от ламинарного к турбулентному. Это значение является максимальным значением числа Рейнольдса, соответствующим полностью разработанному ламинарному течению.

`Turbulent flow lower Reynolds number limit` — Число Рейнольдса, выше которого поток турбулентен
`4e+3` (значение по умолчанию) | положительный безразмерный скаляр

Число Рейнольдса, ниже которого поток трубопровода начинает переходить от турбулентного до ламинарного. Это значение является минимальным числом Рейнольдса, соответствующим полностью разработанному турбулентному течению.

`Shape factor for laminar flow viscous friction` — Безразмерный коэффициент раньше получал эффект геометрии на вязких потерях на трение
64 (значение по умолчанию) | положительный безразмерный скаляр

Безразмерный коэффициент раньше получал эффекты перекрестной частной геометрии на вязких потерях на трение, понесенных в ламинарном режиме течения жидкости. Типичными значениями является 64 для круглого сечения, 57 для квадратного сечения и 62 для прямоугольного сечения с соотношением сторон 2.

Теплопередача

`External environment heat transfer coefficient` — Коэффициент теплопередачи между средой и стеной трубопровода
`100 W/(m^2K)` (значение по умолчанию) | положительная скалярная величина с модулями степени / (areatemperature)

Коэффициент теплопередачи для теплообмена между средой (в порте H) и наружной поверхностью стены трубопровода. Если этот параметр устанавливается на inf, затем тепловое сопротивление между средой и стеной принято, чтобы быть нулем. Стена трубопровода затем имеет универсальную температуру, равную сопоставленному с портом H.

`Wall thickness` — Средняя толщина стенного материала трубопровода
`0 m` (значение по умолчанию) | положительная скалярная величина с единицами длины

Средняя толщина стенного материала трубопровода. Если это значение установлено к 0, затем и тепловое сопротивление из-за проводимости через стену трубопровода и тепловое устройство хранения данных из-за количества тепла стены трубопровода приняты, чтобы быть незначительными.

`Wall thermal conductivity` — Теплопроводность стенного материала трубопровода
`390 W/(mK)` (значение по умолчанию) | положительная скалярная величина с модулями степени / (lengthtemperature)

Теплопроводность стенного материала трубопровода. Если этот параметр устанавливается на inf, затем тепловое сопротивление из-за проводимости через стену трубопровода принято, чтобы быть незначительным.

`Wall specific heat` — Теплоемкость на единицу массы стенного материала трубопровода
`390 J/kg/K` (значение по умолчанию) | положительная скалярная величина с модулями энергии / (mass*temperature)

Теплоемкость на единицу массы стенного материала трубопровода. Если этот параметр устанавливается на 0, затем тепловое устройство хранения данных из-за количества тепла трубопровода принято, чтобы быть незначительным.

`Wall density` — Массовая плотность стенного материала трубопровода
`9e3 kg/m^3` (значение по умолчанию) | положительная скалярная величина с единицами массы/объема

Массовая плотность стенного материала трубопровода. Если этот параметр устанавливается на 0, затем тепловое устройство хранения данных из-за количества тепла стены трубопровода принято, чтобы быть незначительным.

`Ratio of external fins surface area to no-fin surface area` — Отношение площади поверхности теплопередачи с внешними пластинами к этому без
0 (значение по умолчанию) | положительный безразмерный скаляр

Отношение общей площади поверхности теплопередачи пластин на внешней стороне стены трубопровода к той из стены трубопровода без любых пластин. Присутствие пластин служит, чтобы улучшить конвективную теплопередачу между стеной трубопровода и средой.

`External fin efficiency` — Отношение фактических к идеальным уровням теплообмена с внешними пластинами
0.5 (значение по умолчанию) | положительный безразмерный скаляр

Отношение фактического уровня теплообмена между внешними пластинами и средой к ее идеальному значению (если пластины были полностью сохранены при температуре стены трубопровода). Этот параметр является функцией финансовой геометрии.

`Ratio of internal fins surface area to no-fin surface area` — Отношение площади поверхности теплопередачи с внутренними пластинами к этому без
0 (значение по умолчанию) | положительный безразмерный скаляр

Отношение общей площади поверхности теплопередачи пластин на внутренней стороне стены трубопровода к той из стены трубопровода без любых пластин. Присутствие пластин служит, чтобы улучшить конвективную теплопередачу между стеной трубопровода и жидкостью.

`Internal fin efficiency` — Отношение фактических к идеальным уровням теплообмена с внутренними пластинами
0.5 (значение по умолчанию) | положительный безразмерный скаляр

Отношение фактического уровня теплообмена между внутренними пластинами и средой к ее идеальному значению (если пластины были полностью сохранены при температуре стены трубопровода). Этот параметр является функцией финансовой геометрии.

`Nusselt number for laminar flow heat transfer` — Отношение конвективных к проводящим уровням теплообмена в ламинарном режиме течения жидкости
3.66 (значение по умолчанию)

Отношение конвективных к проводящим уровням теплообмена в ламинарном режиме течения жидкости. Этот параметр является функцией геометрии сечения канала. Типичными значениями является 3.66 для круглого сечения, 2.98 для квадратного сечения и 3.39 для прямоугольного сечения с соотношением сторон 2.

Эффекты и вкладка начальных условий

`Initial fluid energy specification` — Термодинамическая переменная, чье начальное значение, чтобы установить
`Temperature` (значение по умолчанию) | `Vapor quality` | `Vapor void fraction` | `Specific enthalpy` | `Specific internal energy`

Термодинамическая переменная, в терминах которой можно задать начальные условия компонента.

`Initial pressure` — Абсолютное давление в начале симуляции
`0.101325 MPa` (значение по умолчанию) | скаляр с единицами давления

Давление в трубопроводе в начале симуляции, заданной против абсолютного нуля.

`Initial temperature` — Абсолютная температура в начале симуляции
`293.15 K` (значение по умолчанию) | скалярный или двухэлементный вектор с единицами температуры

Температура жидкости в трубопроводе в начале симуляции. Этот параметр может быть скаляром или вектором с 2 элементами. Если это - скаляр, начальная температура принята, чтобы быть универсальной в трубопроводе. Если это - вектор, начальная температура принимается линейно зависимой между портами. Первый векторный элемент дает начальную температуру во входе и втором векторном элементе при выходе.

Зависимости

Этот параметр активен, когда опция Initial fluid energy specification установлена в Temperature.

`Initial vapor quality` — Массовая часть пара в начале симуляции
0.5 (значение по умолчанию) | безразмерный скаляр между 0 и 1

Качество пара или массовая часть пара, в трубопроводе в начале симуляции. Этот параметр может быть скаляром или вектором с 2 элементами. Если это - скаляр, начальное качество пара принято, чтобы быть универсальным в трубопроводе. Если это - вектор, начальное качество пара принимается линейно зависимым между портами. Первый векторный элемент дает начальное качество пара во входе и втором векторном элементе при выходе.

Зависимости

Этот параметр активен, когда опция Initial fluid energy specification установлена в Vapor quality.

`Initial vapor void fraction` — Часть объема пара в начале симуляции
0.5 (значение по умолчанию) | безразмерный скаляр между 0 и 1

Пар пусто фракционируется, или часть объема пара, в трубопроводе в начале симуляции. Этот параметр может быть скаляром или вектором с 2 элементами. Если это - скаляр, начальный пар, пустая часть принята, чтобы быть универсальной в трубопроводе. Если это - вектор, начальный пар, пустая часть принимается линейно зависимой между портами. Первый векторный элемент дает начальный пар, пусто фракционируются во входе и втором векторном элементе при выходе..

Зависимости

Этот параметр активен, когда опция Initial fluid energy specification установлена в Vapor void fraction.

`Initial specific enthalpy` — Определенная энтальпия в начале симуляции
`1500 kJ/kg` (значение по умолчанию) | скаляр с модулями энергии/массы

Определенная энтальпия жидкости в трубопроводе в начале симуляции. Этот параметр может быть скаляром или вектором с 2 элементами. Если это - скаляр, начальная определенная энтальпия принята, чтобы быть универсальной в трубопроводе. Если это - вектор, начальная определенная энтальпия принимается линейно зависимой между портами. Первый векторный элемент дает начальную определенную энтальпию во входе и втором векторном элементе при выходе.

Зависимости

Этот параметр активен, когда опция Initial fluid energy specification установлена в Specific enthalpy.

`Initial specific internal energy` — Определенная внутренняя энергия в начале симуляции
`1500 kJ/kg` (значение по умолчанию) | скаляр с модулями энергии/массы

Определенная внутренняя энергия жидкости в трубопроводе в начале симуляции. Этот параметр может быть скаляром или вектором с 2 элементами. Если это - скаляр, начальная определенная внутренняя энергия принята, чтобы быть универсальной в трубопроводе. Если это - вектор, начальная определенная внутренняя энергия принимается линейно зависимой между портами. Первый векторный элемент дает начальную определенную внутреннюю энергию во входе и втором векторном элементе при выходе.

Зависимости

Этот параметр активен, когда опция Initial fluid energy specification установлена в Specific internal energy.

Примеры модели

Pipe Fluid Vaporization and Condensation

Передайте по каналу жидкое испарение и конденсацию

Блок Pipe (2P) С 3 зонами раньше моделировал испарение или конденсацию потока жидкости в трубопроводе. Блок делит внутренний объем жидкости максимум на три зоны: жидкая зона, зона смеси и зона пара, в зависимости от состояния жидкости вдоль трубопровода. Как потоки жидкости через трубопровод, тепло передается между средой, внешней к трубопроводу и жидкостью в трубопроводе, заставляя его измениться от жидкости до смеси, чтобы испариться для нагревающегося случая или от пара до смеси к жидкости для охлаждающегося случая. Эффект теплового устройства хранения данных в стене трубопровода может быть опционально включен путем определения ненулевой толщины стенок трубопровода.

Ссылки

[1] Белый, F.M., гидроаэромеханика, 7^th Эд, разделите 6.8. McGraw-Hill, 2011.

[2] Çengel, Y.A., теплопередача и перемещение массы — практический подход, 3^rd Эд, разделите 8.5. McGraw-Hill, 2007.

Документация

3-Zone Pipe (2P)

Описание

Теплопередача между жидкостью и стеной

Теплопередача между стеной и средой

Баланс импульса

Баланс массы

Энергетический баланс

Допущения и ограничения

Порты

Вывод

Z — Зональные части длины физический сигнал

Сохранение

A — Открытие трубопровода двухфазная жидкость

B — Открытие трубопровода двухфазная жидкость

H — Передайте стену по каналу тепловой

Параметры

Pipe length — Расстояние между портами трубопровода 5 m (значение по умолчанию) | положительная скалярная величина с единицами длины

Cross-sectional area — Внутренняя область, нормальная к направлению потока 0.01 m^2 (значение по умолчанию) | положительная скалярная величина с единицами площади

Laminar flow upper Reynolds number limit — Число Рейнольдса, ниже которого поток ламинарен 2e+3 (значение по умолчанию) | положительный безразмерный скаляр

Turbulent flow lower Reynolds number limit — Число Рейнольдса, выше которого поток турбулентен 4e+3 (значение по умолчанию) | положительный безразмерный скаляр

Wall thickness — Средняя толщина стенного материала трубопровода 0 m (значение по умолчанию) | положительная скалярная величина с единицами длины

Wall density — Массовая плотность стенного материала трубопровода 9e3 kg/m^3 (значение по умолчанию) | положительная скалярная величина с единицами массы/объема

External fin efficiency — Отношение фактических к идеальным уровням теплообмена с внешними пластинами0.5 (значение по умолчанию) | положительный безразмерный скаляр

Internal fin efficiency — Отношение фактических к идеальным уровням теплообмена с внутренними пластинами0.5 (значение по умолчанию) | положительный безразмерный скаляр

Nusselt number for laminar flow heat transfer — Отношение конвективных к проводящим уровням теплообмена в ламинарном режиме течения жидкости3.66 (значение по умолчанию)

Initial pressure — Абсолютное давление в начале симуляции 0.101325 MPa (значение по умолчанию) | скаляр с единицами давления

Initial temperature — Абсолютная температура в начале симуляции 293.15 K (значение по умолчанию) | скалярный или двухэлементный вектор с единицами температуры

Зависимости

Initial vapor quality — Массовая часть пара в начале симуляции0.5 (значение по умолчанию) | безразмерный скаляр между 0 и 1

Зависимости

Initial vapor void fraction — Часть объема пара в начале симуляции0.5 (значение по умолчанию) | безразмерный скаляр между 0 и 1

Зависимости

Initial specific enthalpy — Определенная энтальпия в начале симуляции 1500 kJ/kg (значение по умолчанию) | скаляр с модулями энергии/массы

Зависимости

Initial specific internal energy — Определенная внутренняя энергия в начале симуляции 1500 kJ/kg (значение по умолчанию) | скаляр с модулями энергии/массы

Зависимости

Примеры модели

Передайте по каналу жидкое испарение и конденсацию

Ссылки

Расширенные возможности

Генерация кода C/C++ Генерация кода C и C++ с помощью Simulink® Coder™.

Смотрите также

Документация Simscape Fluids

Поддержка

`Z` — Зональные части длины
физический сигнал

`A` — Открытие трубопровода
двухфазная жидкость

`B` — Открытие трубопровода
двухфазная жидкость

`H` — Передайте стену по каналу
тепловой

`Pipe length` — Расстояние между портами трубопровода
`5 m` (значение по умолчанию) | положительная скалярная величина с единицами длины

`Cross-sectional area` — Внутренняя область, нормальная к направлению потока
`0.01 m^2` (значение по умолчанию) | положительная скалярная величина с единицами площади

`Laminar flow upper Reynolds number limit` — Число Рейнольдса, ниже которого поток ламинарен
`2e+3` (значение по умолчанию) | положительный безразмерный скаляр

`Turbulent flow lower Reynolds number limit` — Число Рейнольдса, выше которого поток турбулентен
`4e+3` (значение по умолчанию) | положительный безразмерный скаляр

`Wall thickness` — Средняя толщина стенного материала трубопровода
`0 m` (значение по умолчанию) | положительная скалярная величина с единицами длины

`Wall density` — Массовая плотность стенного материала трубопровода
`9e3 kg/m^3` (значение по умолчанию) | положительная скалярная величина с единицами массы/объема

`External fin efficiency` — Отношение фактических к идеальным уровням теплообмена с внешними пластинами
0.5 (значение по умолчанию) | положительный безразмерный скаляр

`Internal fin efficiency` — Отношение фактических к идеальным уровням теплообмена с внутренними пластинами
0.5 (значение по умолчанию) | положительный безразмерный скаляр

`Nusselt number for laminar flow heat transfer` — Отношение конвективных к проводящим уровням теплообмена в ламинарном режиме течения жидкости
3.66 (значение по умолчанию)

`Initial pressure` — Абсолютное давление в начале симуляции
`0.101325 MPa` (значение по умолчанию) | скаляр с единицами давления

`Initial temperature` — Абсолютная температура в начале симуляции
`293.15 K` (значение по умолчанию) | скалярный или двухэлементный вектор с единицами температуры

`Initial vapor quality` — Массовая часть пара в начале симуляции
0.5 (значение по умолчанию) | безразмерный скаляр между 0 и 1

`Initial vapor void fraction` — Часть объема пара в начале симуляции
0.5 (значение по умолчанию) | безразмерный скаляр между 0 и 1

`Initial specific enthalpy` — Определенная энтальпия в начале симуляции
`1500 kJ/kg` (значение по умолчанию) | скаляр с модулями энергии/массы

`Initial specific internal energy` — Определенная внутренняя энергия в начале симуляции
`1500 kJ/kg` (значение по умолчанию) | скаляр с модулями энергии/массы

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.