Теплообменник между двумя двухфазными гидросистемами, с основанным на модели на данных о производительности
Simscape / Жидкости / Интерфейсы Гидросистемы / Теплообменники
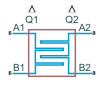
Блок System-Level Heat Exchanger (2P-2P) моделирует теплообменник между двумя отличными двухфазными гидросистемами. Каждая сеть имеет свой собственный набор свойств жидкости.
Модель блока основана на данных о производительности от таблицы данных теплообменника, а не на подробной геометрии обменника, и поэтому можно использовать этот блок, когда данные о геометрии недоступны. Или или обе стороны теплообменника могут уплотнить или выпарить жидкость в результате теплообмена. Можно также использовать этот блок в качестве внутреннего теплообменника в системе охлаждения. Внутренний теплообменник повышает системную эффективность охлаждения путем обеспечения дополнительного теплообмена между выходом конденсатора и выходом испарителя.
Вы параметрируете блок номинальными условиями работы. Теплообменник измерен, чтобы совпадать с заданной эффективностью в номинальных условиях работы в устойчивом состоянии.
Каждая сторона теплообменника аппроксимирует жидкую зону, зону смеси и зону пара на основе изменения в энтальпии вдоль пути к потоку.
Двухфазный жидкий 1 поток и двухфазные жидкие 2 потока каждый разделены на три сегмента равного размера. Теплопередача между жидкостями вычисляется в каждом сегменте. Для простоты уравнение для одного сегмента показывают здесь.
Если стенное количество тепла выключено, то баланс тепла в теплообменнике
где:
Q seg, 2P1 является уровнем теплового потока от стены (то есть, поверхность теплопередачи) к двухфазному жидкому 1 в сегменте.
Q seg, 2P2 является уровнем теплового потока от стены до двухфазных жидких 2 в сегменте.
Если стенное количество тепла включено, то баланс тепла в теплообменнике
где:
Стена M является массой стены.
c pwall является удельной теплоемкостью стены.
N = 3 является количеством сегментов.
T seg, стена является средней температурой стенки в сегменте.
t время.
Уровень теплового потока от стены до двухфазного жидкого 1 в сегменте
где:
UA seg, 2P1 является средневзвешенной проводимостью теплопередачи для двухфазного жидкого 1 в сегменте.
T seg, 2P1 является средневзвешенной температурой жидкости для двухфазного жидкого 1 в сегменте.
Уровень теплового потока от стены до двухфазных жидких 2 в сегменте
где:
UA seg, 2P2 является средневзвешенной проводимостью теплопередачи для двухфазных жидких 2 в сегменте.
T seg, 2P2 является средневзвешенной температурой жидкости для двухфазных жидких 2 в сегменте.
Если сегмент подохлаждается жидкость, то проводимость теплопередачи
где:
a L, 2P1, b 2P1, и c 2P1 является коэффициентами корреляции номера Nusselt. Эти коэффициенты появляются как параметры блоков в разделе Correlation Coefficients.
Re seg, L, 2P1 является средним жидким числом Рейнольдса для сегмента.
Pr seg, L, 2P1 является средним жидким числом Прандтля для сегмента.
k seg, L, 2P1 является средней жидкой теплопроводностью для сегмента.
G 2P1 является масштабным коэффициентом геометрии для двухфазной жидкой 1 стороны теплообменника. Блок вычисляет масштабный коэффициент геометрии так, чтобы общая теплопередача по всем сегментам совпадала с заданной эффективностью в номинальных условиях работы.
Среднее жидкое число Рейнольдса
где:
массовый расход жидкости через сегмент.
μ seg, L, 2P1 является средней жидкой динамической вязкостью для сегмента.
D касательно, 2P1 является произвольным ссылочным диаметром.
S касательно, 2P1 является произвольной ссылочной площадью потока.
Примечание
D касательно, 2P1 и S касательно, 2P1 термины включен в это уравнение в модульных целях вычисления только, чтобы сделать Re seg, L, 2P1 безразмерным. Значения D касательно, 2P1 и S касательно, 2P1 произвольны, потому что G 2P1 вычисление заменяет эти значения.
Точно так же, если сегмент перегрет пар, то проводимость теплопередачи
где:
a V, 2P1, b 2P1, и c 2P1 является коэффициентами корреляции номера Nusselt. Эти коэффициенты появляются как параметры блоков в разделе Correlation Coefficients.
Re seg, V, 2P1 является средним числом Рейнольдса пара для сегмента.
Pr seg, V, 2P1 является средним числом Прандтля пара для сегмента.
k seg, V, 2P1 является средней теплопроводностью пара для сегмента.
Среднее число Рейнольдса пара
где μ seg, V, 2P1 является средним паром динамическая вязкость для сегмента.
Если сегмент является смесью жидкого пара, то проводимость теплопередачи
где:
a M, 2P1, b 2P1, и c 2P1 является коэффициентами корреляции номера Nusselt. Эти коэффициенты появляются как параметры блоков в разделе Correlation Coefficients.
Re seg, SL, 2P1 являются влажным жидким числом Рейнольдса для сегмента.
Pr seg, SL, 2P1 являются влажным жидким числом Прандтля для сегмента.
k seg, SL, 2P1 являются влажной жидкой теплопроводностью для сегмента.
CZ является термином Каваллини и Зеччина.
Влажное жидкое число Рейнольдса
где μ seg, SL, 2P1 являются влажной жидкой динамической вязкостью для сегмента.
Термин Каваллини и Зеччина
где:
ν seg, SL, 2P1 являются влажным жидким определенным объемом для сегмента.
ν seg, SV, 2P1 являются влажным паром определенный объем для сегмента.
x seg, в, 2P1 является качеством пара во входе сегмента.
x seg, 2P1 является качеством пара при выходе сегмента.
Выражение основано на работе Каваллини и Зеччина [5], который выводит содействующую корреляцию теплопередачи в локальном качестве пара x. Уравнения для смеси жидкого пара получены путем усреднения Каваллини и корреляции Зеччина по сегменту от x seg, в, 2P1 к x seg, 2P1.
Двухфазный поток жидкости через сегмент не может быть полностью представлен или как подохлажденный жидкий, перегретый пар или как смесь жидкого пара. Вместо этого каждый сегмент может состоять из комбинации их. Блок аппроксимирует это условие путем вычисления взвешивания факторов на основе изменения в определенной энтальпии через сегмент и влажную жидкость, и испаритесь определенные энтальпии:
где:
h seg, в, 2P1 является определенной энтальпией во входе сегмента.
h seg, 2P1 является определенной энтальпией при выходе сегмента.
h seg, SL, 2P1 являются влажной жидкой определенной энтальпией для сегмента.
h seg, SV, 2P1 являются влажным паром определенная энтальпия для сегмента.
Средневзвешенная двухфазная жидкая 1 проводимость теплопередачи для сегмента поэтому
Средневзвешенная жидкая 1 температура для сегмента
где:
T seg, L, 2P1 является средней жидкой температурой для сегмента.
T seg, V, 2P1 является средней температурой пара для сегмента.
T seg, M, 2P1 является средней температурой смеси для сегмента, который является влажной жидкой температурой.
Если сегмент подохлаждается жидкость, то проводимость теплопередачи
где:
a L, 2P2, b L, 2P2, и c L, 2P2 является коэффициентами корреляции номера Nusselt. Эти коэффициенты появляются как параметры блоков в разделе Correlation Coefficients.
Re seg, L, 2P2 является средним жидким числом Рейнольдса для сегмента.
Pr seg, L, 2P2 является средним жидким числом Прандтля для сегмента.
k seg, L, 2P2 является средней жидкой теплопроводностью для сегмента.
G 2P2 является масштабным коэффициентом геометрии для двухфазных жидких 2 сторон теплообменника. Блок вычисляет масштабный коэффициент геометрии так, чтобы общая теплопередача по всем сегментам совпадала с заданной эффективностью в номинальных условиях работы.
Среднее жидкое число Рейнольдса
где:
массовый расход жидкости через сегмент.
μ seg, L, 2P2 является средней жидкой динамической вязкостью для сегмента.
D касательно, 2P2 является произвольным ссылочным диаметром.
S касательно, 2P2 является произвольной ссылочной площадью потока.
Примечание
D касательно, 2P2 и S касательно, 2P2 термины включен в это уравнение в модульных целях вычисления только, чтобы сделать Re seg, L, 2P2 безразмерным. Значения D касательно, 2P и S касательно, 2P2 произвольны, потому что G 2P2 вычисление заменяет эти значения.
Точно так же, если сегмент перегрет пар, то проводимость теплопередачи
где:
a V, 2P2, b V, 2P2, и c V, 2P2 является коэффициентами корреляции номера Nusselt. Эти коэффициенты появляются как параметры блоков в разделе Correlation Coefficients.
Re seg, V, 2P2 является средним числом Рейнольдса пара для сегмента.
Pr seg, V, 2P2 является средним числом Прандтля пара для сегмента.
k seg, V, 2P2 является средней теплопроводностью пара для сегмента.
Среднее число Рейнольдса пара
где μ seg, V, 2P2 является средним паром динамическая вязкость для сегмента.
Если сегмент является смесью жидкого пара, то проводимость теплопередачи
где:
a M, 2P2, b L, 2P2, и c L, 2P2 является коэффициентами корреляции номера Nusselt. Эти коэффициенты появляются как параметры блоков в разделе Correlation Coefficients.
Re seg, SL, 2P2 являются влажным жидким числом Рейнольдса для сегмента.
Pr seg, SL, 2P2 являются влажным жидким числом Прандтля для сегмента.
k seg, SL, 2P2 являются влажной жидкой теплопроводностью для сегмента.
CZ является термином Каваллини и Зеччина.
Влажное жидкое число Рейнольдса
где μ seg, SL, 2P2 являются влажной жидкой динамической вязкостью для сегмента.
Термин Каваллини и Зеччина
где:
ν seg, SL, 2P2 являются влажным жидким определенным объемом для сегмента.
ν seg, SV, 2P2 являются влажным паром определенный объем для сегмента.
x seg, в, 2P2 является качеством пара во входе сегмента.
x seg, 2P2 является качеством пара при выходе сегмента.
Выражение основано на работе Каваллини и Зеччина [5], который выводит содействующую корреляцию теплопередачи в локальном качестве пара x. Уравнения для смеси жидкого пара получены путем усреднения Каваллини и корреляции Зеччина по сегменту от x seg, в, 2P2 к x seg, 2P2.
Двухфазный поток жидкости через сегмент не может быть полностью представлен или как подохлажденный жидкий, перегретый пар или как смесь жидкого пара. Вместо этого каждый сегмент может состоять из комбинации их. Блок аппроксимирует это условие путем вычисления взвешивания факторов на основе изменения в определенной энтальпии через сегмент и влажную жидкость, и испаритесь определенные энтальпии:
где:
h seg, в, 2P2 является определенной энтальпией во входе сегмента.
h seg, 2P2 является определенной энтальпией при выходе сегмента.
h seg, SL, 2P2 являются влажной жидкой определенной энтальпией для сегмента.
h seg, SV, 2P2 являются влажным паром определенная энтальпия для сегмента.
Средневзвешенные двухфазные жидкие 2 проводимости теплопередачи для сегмента поэтому
Средневзвешенные жидкие 2 температуры для сегмента
где:
T seg, L, 2P2 является средней жидкой температурой для сегмента.
T seg, V, 2P2 является средней температурой пара для сегмента.
T seg, M, 2P2 является средней температурой смеси для сегмента, который является влажной жидкой температурой.
Падение давления на двухфазной жидкой 1 стороне
где:
p A, 2P1 и p B, 2P1 является давлениями в портах A1 и B1, соответственно.
p 2P1 является внутренним двухфазным жидким 1 давлением, при котором вычисляется теплопередача.
и массовые расходы жидкости в порты A1 и B1, соответственно.
ρ в среднем, 2P1 является средней двухфазной жидкой 1 плотностью по всем сегментам.
ламинарный порог для падения давления, аппроксимированного как 1e-4 номинального массового расхода жидкости. Блок вычисляет коэффициент падения давления, K 2P1, так, чтобы p A, 2P1 – p B, 2P1 совпадал с номинальным падением давления в номинальном массовом расходе жидкости.
Падение давления на двухфазных жидких 2 сторонах
где:
p A, 2P2 и p B, 2P2 является давлениями в портах A2 и B2, соответственно.
p 2P2 является внутренними двухфазными жидкими 2 давлениями, при которых вычисляется теплопередача.
и массовые расходы жидкости в порты A2 и B2, соответственно.
ρ в среднем, 2P2 является средними двухфазными жидкими 2 плотностью по всем сегментам.
ламинарный порог для падения давления, аппроксимированного как 1e-4 номинального массового расхода жидкости. Блок вычисляет коэффициент падения давления, K 2P2, так, чтобы p A, 2P2 – p B, 2P2 совпадал с номинальным падением давления в номинальном массовом расходе жидкости.
Массовое уравнение сохранения для полного двухфазного жидкого 1 потока
где:
частная производная плотности относительно давления для сегмента.
частная производная плотности относительно определенной внутренней энергии для сегмента.
u seg, 2P1 является определенной внутренней энергией для сегмента.
V 2P1 является общим двухфазным жидким 1 объемом.
Суммирование по всем сегментам.
Примечание
Несмотря на то, что двухфазный жидкий 1 поток разделен на N =3 сегмента для вычислений теплопередачи, все сегменты приняты, чтобы быть при том же внутреннем давлении, p 2P1. Именно поэтому p 2P1 находится вне суммирования.
Уравнение энергосбережения для каждого сегмента
где:
M 2P1 является общей двухфазной жидкой 1 массой.
и массовые расходы жидкости в и из сегмента.
Φ seg, в, 2p1 и Φ seg, 2p1 является энергетическими скоростями потока жидкости в и из сегмента.
Массовые расходы жидкости между сегментами приняты, чтобы быть линейно распределенными между значениями и .
Массовое уравнение сохранения для полных двухфазных жидких 2 потоков
где:
частная производная плотности относительно давления для сегмента.
частная производная плотности относительно определенной внутренней энергии для сегмента.
u seg, 2P2 является определенной внутренней энергией для сегмента.
V 2P2 является общими двухфазными жидкими 2 объемами.
Суммирование по всем сегментам.
Примечание
Несмотря на то, что двухфазные жидкие 2 потока разделены на N =3 сегмента для вычислений теплопередачи, все сегменты приняты, чтобы быть при том же внутреннем давлении, p 2P2. Именно поэтому p 2P2 находится вне суммирования.
Уравнение энергосбережения для каждого сегмента
где:
M 2P2 является общими двухфазными жидкими 2 массами.
и массовые расходы жидкости в и из сегмента.
Φ seg, в, 2p2 и Φ seg, 2p2 является энергетическими скоростями потока жидкости в и из сегмента.
Массовые расходы жидкости между сегментами приняты, чтобы быть линейно распределенными между значениями и .