Полиномиальные доверительные интервалы
Y = polyconf(p,X)
[Y,DELTA] = polyconf(p,X,S)
[Y,DELTA] = polyconf(p,X,S,param1,val1,param2,val2,...)
Y = polyconf(p,X) оценивает полиномиальный p в значениях в XP вектор из коэффициентов в убывающих степенях.
[Y,DELTA] = polyconf(p,X,S) берет выходные параметры p и S от polyfit и генерирует 95% интервалов предсказания Y ± DELTA для новых наблюдений в значениях в X.
[Y,DELTA] = polyconf(p,X,S, задает дополнительное название параметра / пары значения, выбранные из следующего списка.param1,val1,param2,val2,...)
| Параметр | Значение |
|---|---|
'alpha' | Значение между 0 и 1 определением доверительного уровня |
'mu' | Двухэлементный вектор, содержащий центрирование и масштабные коэффициенты. При использовании этой опции, |
'predopt' | Любой |
'simopt' | Любой |
'predopt' и 'simopt' параметры могут быть изучены в терминах следующих функций:
p (x) — неизвестная средняя функция оценивается подгонкой
l (x) — более низкая доверительная граница
u (x) — верхняя доверительная граница
Предположим, что вы делаете новое наблюдение y n +1 в x n +1, так, чтобы
y n +1 (x n +1) = p (x n +1) + ε n +1
По умолчанию, интервал [l n +1 (x n +1), u n +1 (x n +1)] является 95%-й доверительной границей на y n +1 (x n +1).
Следующие комбинации 'predopt' и 'simopt' параметры позволяют вам задавать другие границы.
'simopt' | 'predopt' | Ограниченная величина |
|---|---|---|
'off' | 'observation' | y n +1 (x n +1) (значение по умолчанию) |
'off' | 'curve' | p (x n +1) |
'on' | 'observation' | y n +1 (x), для всего x |
'on' | 'curve' | p (x), для всего x |
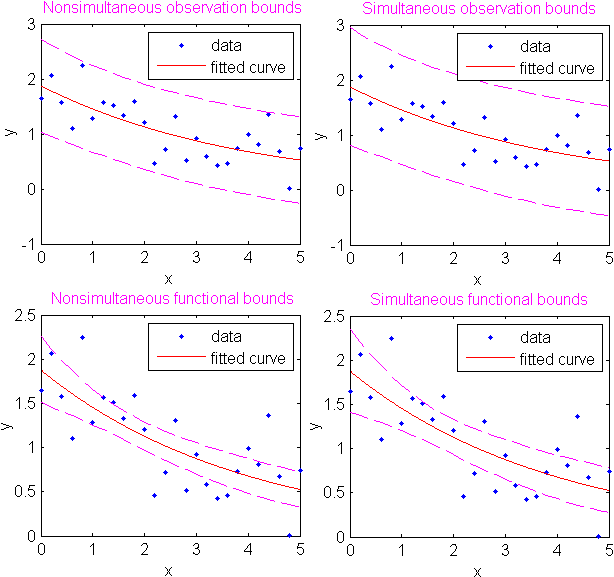
В общем случае 'observation' интервалы более широки, чем 'curve' интервалы, из-за дополнительной неопределенности в предсказании нового значения отклика (кривая плюс случайные ошибки). Аналогично, одновременные интервалы более широки, чем неодновременные интервалы из-за дополнительной неопределенности в ограничении значений для всех предикторов x.
Соответствуйте полиному к набору выборочных данных и оцените 95% интервалов предсказания и корней подходящего полинома. Отобразите на графике данные и оценки, и отобразите подходящее многочленное выражение с помощью функции помощника polystr, чей код появляется в конце этого примера.
Сгенерируйте точки выборочных данных (x,y) с квадратичным трендом.
rng('default') % For reproducibility x = -5:5; y = x.^2 - 20*x - 3 + 5*randn(size(x));
Соответствуйте второму полиному степени к данным при помощи polyfit.
degree = 2; % Degree of the fit
[p,S] = polyfit(x,y,degree);Оцените 95% интервалов предсказания при помощи polyconf.
alpha = 0.05; % Significance level [yfit,delta] = polyconf(p,x,S,'alpha',alpha);
Отобразите на графике данные, адаптированный полином и интервалы предсказания. Отобразите подходящее многочленное выражение с помощью функции помощника polystr.
plot(x,y,'b+') hold on plot(x,yfit,'g-') plot(x,yfit-delta,'r--',x,yfit+delta,'r--') legend('Data','Fit','95% Prediction Intervals') title(['Fit: ',texlabel(polystr(round(p,2)))]) hold off
Найдите корни полиномиального p.
r = roots(p)
r = 2×1
17.5152
-0.1017
Поскольку корни являются вещественными значениями, можно построить их также. Оцените подходящие значения и интервалы предсказания для x интервала, который включает корни. Затем постройте корни и оценки.
if isreal(r) xmin = min([r(:);x(:)]); xrange = range([r(:);x(:)]); xExtended = linspace(xmin - 0.1*xrange, xmin + 1.1*xrange,1000); [yfitExtended,deltaExtended] = polyconf(p,xExtended,S,'alpha',alpha); plot(x,y,'b+') hold on plot(xExtended,yfitExtended,'g-') plot(r,zeros(size(r)),'ko') plot(xExtended,yfitExtended-deltaExtended,'r--') plot(xExtended,yfitExtended+deltaExtended,'r--') plot(xExtended,zeros(size(xExtended)),'k-') legend('Data','Fit','Roots of Fit','95% Prediction Intervals') title(['Fit: ',texlabel(polystr(round(p,2)))]) axis tight hold off end
В качестве альтернативы можно использовать polytool для интерактивного полиномиального подбора кривой.
polytool(x,y,degree,alpha)
Функция помощника
polystr.m файл задает polystr функция помощника.
type polystr.m % Display contents of polystr.m file
function s = polystr(p)
% POLYSTR Converts a vector of polynomial coefficients to a character string.
% S is the string representation of P.
if all(p == 0) % All coefficients are 0.
s = '0';
else
d = length(p) - 1; % Degree of polynomial.
s = []; % Initialize s.
for a = p
if a ~= 0 % Coefficient is nonzero.
if ~isempty(s) % String is not empty.
if a > 0
s = [s ' + ']; % Add next term.
else
s = [s ' - ']; % Subtract next term.
a = -a; % Value to subtract.
end
end
if a ~= 1 || d == 0 % Add coefficient if it is ~=1 or polynomial is constant.
s = [s num2str(a)];
if d > 0 % For nonconstant polynomials, add *.
s = [s '*'];
end
end
if d >= 2 % For terms of degree > 1, add power of x.
s = [s 'x^' int2str(d)];
elseif d == 1 % No power on x term.
s = [s 'x'];
end
end
d = d - 1; % Increment loop: Add term of next lowest degree.
end
end
end