Exponenta Banner

Сердечно-сосудистая модель с разрывами

Этот пример показывает, как использовать dde23, чтобы решить сердечно-сосудистую модель, которая имеет прерывистую производную, как представлено Оттесеном [1].

Нажмите ddex2.m или введите edit ddex2.m в командном окне, чтобы просмотреть код для этого примера в редакторе.

Это - проблема с 1 задержкой, постоянной историей и 3 дифференциальными уравнениями с 14 физическими параметрами. Система в большой степени под влиянием периферийного давления, R, который уменьшается экспоненциально с 1,05 до 0,84, начинаясь в t = 600. В результате система имеет разрыв в производной младшего разряда в t = 600.

  1. Создайте новый программный файл в редакторе. Этот файл будет содержать основную функцию и вложенную функцию. Основная функция не принимает входных параметров и не возвращает выходных параметров.

  2. Задайте физические параметры. Добавьте этот код к основной функции.

    p.ca     = 1.55;
p.cv     = 519;
p.R      = 1.05;
p.r      = 0.068;
p.Vstr   = 67.9;
p.alpha0 = 93;
p.alphas = 93;
p.alphap = 93;
p.alphaH = 0.84;
p.beta0  = 7;
p.betas  = 7;
p.betap  = 7;
p.betaH  = 1.17;
p.gammaH = 0;

  3. Задайте историю решения. Добавьте этот код к основной функции.

    P0 = 93;
Paval = P0;
Pvval = (1 / (1 + p.R/p.r)) * P0;
Hval = (1 / (p.R * p.Vstr)) * (1 / (1 + p.r/p.R)) * P0;
history = [Paval; Pvval; Hval];

  4. Задайте задержку, tau. Добавьте этот код к основной функции.

    tau = 4;

  5. Задайте местоположение разрыва, который происходит в t = 600. Добавьте этот код к основной функции.

    options = ddeset('Jumps',600);

    Когда ваш DDE имеет разрывы в производных младшего разряда, и вы знаете местоположения заранее, лучше использовать ddeset со свойством Jumps.

  6. Решите DDE на интервале [0, 1000]. Добавьте этот код к основной функции.

    sol = dde23(@ddex2de,tau,history,[0,1000],options);

    Функция, @ddex2de, который задает систему DDEs, является первым входным параметром. Вы задаете эту функцию на шаге 8.

  7. Постройте график решения. Добавьте этот код к основной функции.

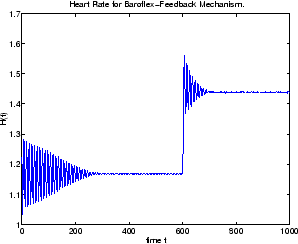
    figure
plot(sol.x,sol.y(3,:))
title('Heart Rate for Baroflex-Feedback Mechanism.')
xlabel('time t')
ylabel('H(t)')

  8. Задайте систему DDEs как вложенная функция в основной функции.

    function dydt = ddex2de(t,y,Z)
    if t <= 600
      p.R = 1.05;
    else
      p.R = 0.21 * exp(600-t) + 0.84;
    end    
    ylag = Z(:,1);
    Patau = ylag(1);
    Paoft = y(1);
    Pvoft = y(2);
    Hoft  = y(3);

    dPadt = - (1 / (p.ca * p.R)) * Paoft ...
            + (1/(p.ca * p.R)) * Pvoft ...
            + (1/p.ca) * p.Vstr * Hoft;

    dPvdt = (1 / (p.cv * p.R)) * Paoft...
            - ( 1 / (p.cv * p.R)...
            + 1 / (p.cv * p.r) ) * Pvoft;

    Ts = 1 / ( 1 + (Patau / p.alphas)^p.betas );
    Tp = 1 / ( 1 + (p.alphap / Paoft)^p.betap );

    dHdt = (p.alphaH * Ts) / (1 + p.gammaH * Tp) ...
           - p.betaH * Tp;

    dydt = [ dPadt; dPvdt; dHdt];
  end

    Эта функция вкладывается так, чтобы основная функция могла получить доступ к этим 14 параметрам, заданным на шаге 2.

  9. Запустите свою программу, чтобы вычислить решение и отобразить график.

Ссылки

[1] Оттесен, J. T. “Моделирование Механизма Baroflex-обратной-связи с Задержкой. J. Математика. Biol. Издание 36, Номер 1, 1997, стр 41–63.

Связанные примеры

Больше о

Была ли эта тема полезной?
Документация MATLAB
Поддержка