Exponenta Banner

DDE нейтрального типа

Этот пример показывает, как использовать ddensd, чтобы решить нейтральный DDE, представленный Полом [1] для 0 ≤ t ≤ π.

Нажмите ddex4.m или введите edit ddex4.m в командном окне, чтобы просмотреть код для этого примера в редакторе.

Уравнение

y' (t) = 1 + y (t) – 2 года (t/2) 2 – y' (t – π)

с историей:

y (t) =, потому что (t) для t ≤ 0.

  1. Создайте новый программный файл в редакторе. Этот файл будет содержать основную функцию и четыре локальных функции.

  2. Задайте DDE первого порядка как локальную функцию.

    function yp = ddefun(t,y,ydel,ypdel) 
    yp = 1 + y - 2*ydel^2 - ypdel;
end

  3. Задайте задержку решения как локальную функцию.

    function dy = dely(t,y) 
    dy = t/2;
end

  4. Задайте производную задержку как локальную функцию.

    function dyp = delyp(t,y) 
    dyp = t-pi;
end

  5. Задайте историю решения как локальную функцию.

    function y = history(t)
    y = cos(t);
end

  6. Задайте интервал интегрирования и решите DDE с помощью функции ddensd. Добавьте этот код к основной функции.

    tspan = [0 pi];
sol = ddensd(@ddefun,@dely,@delyp,@history,tspan);

  7. Оцените решение в 100 равномерно распределенных точках между 0 и π. Добавьте этот код к основной функции.

    tn = linspace(0,pi);
yn = deval(sol,tn);

  8. Постройте график результатов. Добавьте этот код к основной функции.

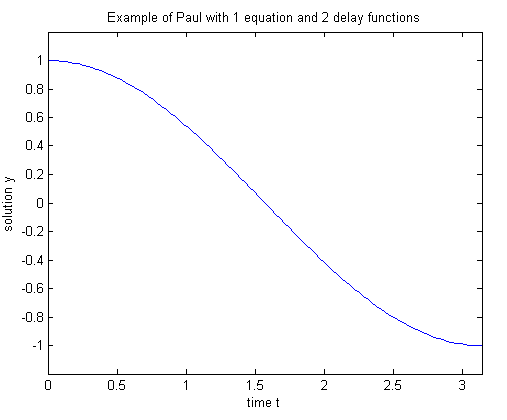
    figure
plot(tn,yn);
xlim([0 pi]);
ylim([-1.2 1.2])
xlabel('time t');
ylabel('solution y');
title('Example of Paul with 1 equation and 2 delay functions')

  9. Запустите свою программу, чтобы вычислить решение и отобразить график.

Ссылки

[1] Пол, C.A.H. “Набор тестов функциональных дифференциальных уравнений”. Числовые аналитические отчеты. № 243. Манчестер, Великобритания: математический отдел, Манчестерский университет, 1994.

Связанные примеры

Больше о

Была ли эта тема полезной?
Документация MATLAB
Поддержка