Exponenta Banner

Проблема задержки состояния зависимая

Этот пример показывает, как использовать ddesd, чтобы решить систему двух DDEs с задержкой состояния зависимой. Эта система DDEs использовалась в качестве тестовой задачи Энрайтом и Хаяши [1].

Нажмите ddex3.m или введите edit ddex3.m в командном окне, чтобы просмотреть полный код для этого примера в редакторе.

Уравнения для этой системы:

y1  (t) =y2 (t) y2  (t) = −y2 (e (1−y2 (т))) ⋅y2 (t) 2⋅e (1−y2 (т)).

Аналитическое решение

y1 (t) =log (t) y2 (t) =1/t

используется в качестве истории для t ≤ 0.1, и уравнения решены на [0.1, 5] с ddesd, а не dde23. Функция ddesd является соответствующей в этом случае, потому что первый фактор во втором уравнении имеет форму y2 (d (y)) с задержкой, которая зависит от второго компонента решения.

  1. Создайте новый программный файл в редакторе. Этот файл будет содержать основную функцию и три локальных функции.

  2. Закодируйте систему DDEs как локальная функция.

    function dydt = ddex3de(t,y,Z)
  dydt = [y(2); -Z(2)*y(2)^2*exp(1 - y(2))];
end

  3. Задайте задержку как локальную функцию.

    function d = ddex3delay(t,y)
  d = exp(1 - y(2));
end

  4. Задайте историю решения как локальную функцию.

    function v = ddex3hist(t)  
  v = [log(t); 1./t];
end

  5. Задайте интервал интегрирования и решите систему. Добавьте этот код к основной функции в вашем программном файле.

    tspan = [0.1 5];
sol = ddesd(@ddex3de,@ddex3delay,@ddex3hist,tspan);

  6. Используйте функцию истории, чтобы вычислить аналитическое решение в интервале интегрирования. Добавьте этот код к основной функции.

    texact = linspace(0.1,5);
yexact = ddex3hist(texact);

  7. Постройте график числового решения на тех же осях как аналитическое решение. Добавьте этот код к основной функции.

    figure
plot(texact,yexact,sol.x,sol.y,'o')
legend('y_1, exact','y_2, exact','y_1, ddesd','y_2, ddesd')
xlabel('time t')
ylabel('solution y')
title('D1 problem of Enright and Hayashi')

  8. Запустите свою программу, чтобы сгенерировать и построить график результатов.

Ссылки

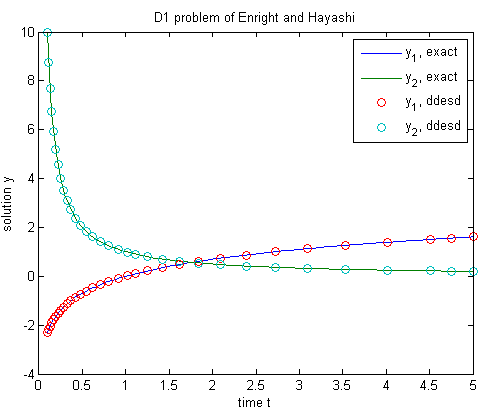
[1] Энрайт, W.H. и Х. Хаяши. “Оценка Числового программного обеспечения для Дифференциальных уравнений с запаздывающим аргументом”. В Продолжениях IFIP TC2/WG2.5 рабочая конференция по Качеству числового программного обеспечения: оценка и улучшение. R. F. Boisvert, редактор). Лондон, Великобритания: Chapman & Hall, Ltd., стр 179-193.

Связанные примеры

Больше о

Была ли эта тема полезной?
Документация MATLAB
Поддержка