Этот пример показывает, как использовать ddensd, чтобы решить DDE начального значения, представленный Jackiewicz [1] для 0 ≤ t ≤ 0.1.
Нажмите ddex5.m или введите edit ddex5.m в командном окне, чтобы просмотреть код для этого примера в редакторе.
Уравнение
y' (t) = 2cos (2 т) y (t/2) 2cos (т) + журнал (y' (t/2)) – журнал (2cos (т)) – грех (t).
Это - DDE начального значения, потому что задержки являются нулем в t0. Начальные условия:
y (0) = 1
y' (0) = s,
2 + журнал (журналы) – журнал (2) = 0.
Создайте новый программный файл в редакторе. Этот файл будет содержать основную функцию и одну локальную функцию.
Задайте DDE как локальную функцию.
function yp = ddefun(t,y,ydel,ypdel) yp=2*cos(2*t)*ydel^(2*cos(t))+log(ypdel)-log(2*cos(t))-sin(t); end
Задайте задержку решения и производную задержку. Добавьте эту строку к основной функции.
delay = @(t,y) t/2;
Можно использовать одну анонимную функцию, чтобы обработать обе задержки, поскольку они - то же самое в уравнении.
Задайте начальные условия, y0 и s1 и интервал интегрирования, tspan. Добавьте этот код к основной функции.
y0 = 1; s1 = 2; tspan = [0 0.1];
Решите DDE для 0 ≤ t ≤ 0.1 с начальными условиями y (0) = 1 и y' (0) = 2. Добавьте этот код к основной функции.
sol1 = ddensd(@ddefun,delay,delay,{y0,s1},tspan);Решите уравнение снова, на этот раз с помощью y' (0) = 0.4063757399599599. Добавьте этот код к основной функции.
s2 = 0.4063757399599599;
sol2 = ddensd(@ddefun,delay,delay,{y0,s2},tspan);Постройте график результатов. Добавьте этот код к основной функции.
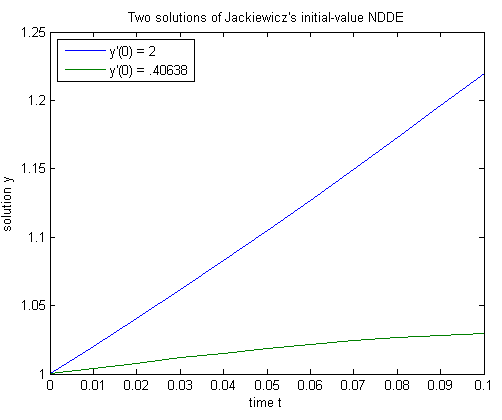
figure plot(sol1.x,sol1.y,sol2.x,sol2.y); legend('y''(0) = 2','y''(0) = .40638','Location','NorthWest'); xlabel('time t'); ylabel('solution y'); title('Two solutions of Jackiewicz''s initial-value NDDE');
Запустите свою программу, чтобы вычислить и построить график решений для каждого значения s.
[1] Jackiewicz, Z. “Методы шага любого Порядка для Нейтральных Функциональных Дифференциальных уравнений”. SIAM J. Numer. Анальный. Издание 21, Номер 3. 1984. стр 486–511.