bvp4c

Решите краевые задачи для обыкновенных дифференциальных уравнений

Синтаксис

sol = bvp4c (odefun, bcfun, solinit) sol = bvp4c (odefun, bcfun, solinit, опции) solinit = bvpinit (x, yinit, параметрические усилители)

Аргументы

`odefun`	Указатель на функцию, который оценивает дифференциальные уравнения f (x, y). Это может иметь форму dydx = odefun(x,y) dydx = odefun(x,y,parameters) Для скалярного `x` и вектора - столбца `y`, `odefun(x,y)` должен возвратить вектор - столбец, `dydx`, представляя f (x, y). `parameters` является вектором неизвестных параметров.
`bcfun`	Указатель на функцию, который вычисляет невязку в граничных условиях. Для условий граничного значения двух-точки формы до н.э (y (a), y (b)), `bcfun` может иметь форму res = bcfun(ya,yb) res = bcfun(ya,yb,parameters) где `ya` и `yb` являются векторами - столбцами, соответствующими y (a) и y (b). `parameters` является вектором неизвестных параметров. Вывод `res` является вектором - столбцом. См. Многоточечные Краевые задачи для описания `bcfun` для многоточечных краевых задач.
`solinit`	Структура, содержащая исходное предположение для решения. Вы создаете `solinit` с помощью функционального `bvpinit`. `solinit` имеет следующие поля.
	`x`	Заказанные узлы начальной mesh. Граничные условия наложены в = `solinit.x(1)` и b = `solinit.x(end)`.
	`y`	Исходное предположение для решения, таким образом, что `solinit.y(:,i)` является предположением для решения в узле `solinit.x(i)` .
	`параметры`	Дополнительный. Вектор, который обеспечивает исходное предположение для неизвестных параметров.
	Структура может иметь любое имя, но поля нужно назвать `x`, `y` и `parameters`. Можно сформировать `solinit` с функцией помощника `bvpinit`. Смотрите `bvpinit` для деталей.
`опции`	Дополнительный аргумент интегрирования. Структура вы создаете использование функции `bvpset`. Смотрите `bvpset` для деталей.

Описание

sol = bvp4c(odefun,bcfun,solinit) интегрирует систему обыкновенных дифференциальных уравнений формы

y ′ = f (x, y)

на интервале [a, b] подвергают, чтобы двух-указать условия граничного значения до н.э (y (a), y (b)) = 0.

odefun и bcfun являются указателями на функцию. См. Создание указателя на функцию для получения дополнительной информации.

Параметризация Функций объясняет, как предоставить дополнительные параметры функциональному odefun, а также функцию граничного условия bcfun, при необходимости.

bvp4c может также решить многоточечные краевые задачи. См. Многоточечные Краевые задачи. Можно использовать функциональный bvpinit, чтобы задать граничные точки, которые сохранены во входном параметре solinit. Смотрите страницу с описанием для bvpinit для получения дополнительной информации.

Решатель bvp4c может также найти неизвестные параметры p для проблем формы

y ′ = f (x, y, p)

0 = до н.э (y (a), y (b), p)

где p соответствует parameters. Вы предоставляете bvp4c исходное предположение для любых неизвестных параметров в solinit.parameters параметры. Решатель bvp4c возвращает окончательные значения этих неизвестных параметров в sol.parameters параметры.

bvp4c производит решение, которое непрерывно на [a,b] и имеет непрерывную первую производную там. Используйте функциональный deval и вывод sol bvp4c, чтобы оценить решение в отдельных моментах xint в интервале [a,b].

sxint = deval(sol,xint)

Структура sol, возвращенный bvp4c, имеет следующие поля:

`sol.x`	Mesh выбрана `bvp4c`
`sol.y`	Приближение к y (x) в точках mesh `sol.x`
`sol.yp`	Приближение к y ′ (x) в точках mesh `sol.x`
`sol.parameters`	Значения`, возвращенные bvp4c` для неизвестных параметров, если любой
`sol.solver`	`bvp4c`
`sol.stats`	Вычислительная статистика стоимости (также отображенный, когда опция `stats` установлена с `bvpset`).

Структура sol может иметь любое имя и bvp4c, создает поля x, y, yp, parameters и solver.

sol = bvp4c(odefun,bcfun,solinit,options) решает как выше со свойствами интегрирования по умолчанию, замененными значениями в options, структура, созданная с функцией bvpset. Смотрите bvpset для деталей.

solinit = bvpinit(x, yinit, params) формирует исходное предположение solinit с векторным params предположений для неизвестных параметров.

Сингулярные Краевые задачи

bvp4c решает класс сингулярных краевых задач, включая проблемы с неизвестными параметрами p, формы

y ′ = S · y/x + F (x, y, p)

0 = до н.э (y (0), y (b), p)

Интервал требуется, чтобы быть [0, b] с b> 0. Часто такие проблемы возникают при вычислении сглаженного решения ОДУ, которые следуют из дифференциальных уравнений с частными производными (УЧП) из-за цилиндрической или сферической симметрии. Для сингулярных проблем вы задаете (постоянный) матричный S как значение опции 'SingularTerm' bvpset, и odefun оценивает только f (x, y, p). Граничные условия должны быть сопоставимы с необходимым условием S · y (0) = 0 и исходное предположение должен удовлетворить это условие.

Многоточечные Краевые задачи

bvp4c может решить многоточечные краевые задачи, где = a0 < a1 < a2 < ... < = b являются граничными точками в интервале [a, b]. Точки a1, a2..., an−1 представляют интерфейсы, которые делятся [a, b] в области. bvp4c перечисляет области слева направо (от до b) с индексами, запускающимися от 1. В области k, [ak−1, ak], bvp4c оценивает производную как

yp = odefun(x,y,k)

В функции граничных условий

bcfun(yleft,yright)

yleft(:,k) является решением на левом контуре [ak−1, ak]. Точно так же yright(:,k) является решением на правильном контуре области k. В частности,

yleft(:,1) = y(a)

yright(:,end) = y(b)

Когда вы создаете исходное предположение с

solinit = bvpinit(xinit,yinit),

используйте двойные записи в xinit для каждой интерфейсной точки. Смотрите страницу с описанием для bvpinit для получения дополнительной информации.

Если yinit является функцией, bvpinit вызывает y = yinit(x,k), чтобы получить исходное предположение для решения в x в области k. В структуре решения sol, возвращенный bpv4c, sol.x имеет двойные записи для каждой интерфейсной точки. Соответствующие столбцы sol.y содержат левое и правое решение в интерфейсе, соответственно.

Чтобы видеть пример, который решает краевую задачу с тремя точками, введите threebvp в командной строке ^MATLAB®.

Примечание

Функция bvp5c используется точно как bvp4c, за исключением значения ошибочных допусков между этими двумя решателями. Если S (x) аппроксимирует решение y (x), bvp4c управляет невязкой |S ′ (x) – f (x, S (x)) |. Это управляет косвенно истинной погрешностью |y (x) – S (x) |. bvp5c управляет истинной погрешностью непосредственно.

Примеры

Используя исходное предположение, чтобы указать на требуемое решение

Краевые задачи могут иметь несколько решений. Одна цель исходного предположения состоит в том, чтобы указать, какое решение, среди нескольких, которые вы хотите.

Дифференциальное уравнение второго порядка

имеет точно два решения, которые удовлетворяют граничные условия

Перед использованием bvp4c, чтобы решить проблему, необходимо переписать дифференциальное уравнение как систему двух ОДУ первого порядка,

где и. Эта система имеет необходимую форму

Функция, f, и граничные условия, до н.э, закодирована в MATLAB как функции twoode и twobc.

function dydx = twoode(x,y)
dydx = [ y(2); -abs(y(1)) ];

function res = twobc(ya,yb)
res = [ ya(1); yb(1) + 2 ];

Сформируйте структуру предположения, состоящую из начальной сетки пяти равномерно распределенных точек в [0,4] и предположение постоянных значений

solinit = bvpinit(linspace(0,4,5),[1 0]);

Решите проблему с помощью bvp4c.

sol = bvp4c(@twoode,@twobc,solinit);

Оцените числовое решение в 100 равномерно распределенных точках и постройте график y (x).

x = linspace(0,4);
y = deval(sol,x);
plot(x,y(1,:))

Чтобы получить другое решение этой проблемы, используйте исходное предположение

solinit = bvpinit(linspace(0,4,5),[-1 0]);
sol = bvp4c(@twoode,@twobc,solinit);
x = linspace(0,4);
y = deval(sol,x);
plot(x,y(1,:))

Вычисление четвертого собственного значения уравнения Мэтью

Эта краевая задача включает неизвестный параметр. Задача состоит в том, чтобы вычислить четвертое (q = 5) собственное значение λ уравнения Мэтью

y” + (λ – 2q cos2x) y = 0.

Поскольку неизвестный параметр λ присутствует, это дифференциальное уравнение второго порядка подчиняется трем граничным условиям:

y ′ (0) = 0

y ′ (π) = 0

y (0) = 1

Удобно использовать локальные функции, чтобы поместить все функции, требуемые bvp4c в единственном файле.

function mat4bvp

lambda = 15;
solinit = bvpinit(linspace(0,pi,10),@mat4init,lambda);
sol = bvp4c(@mat4ode,@mat4bc,solinit);

fprintf('The fourth eigenvalue is approximately %7.3f.\n',...
        sol.parameters)

xint = linspace(0,pi);
Sxint = deval(sol,xint);
plot(xint,Sxint(1,:))
axis([0 pi -1 1.1])
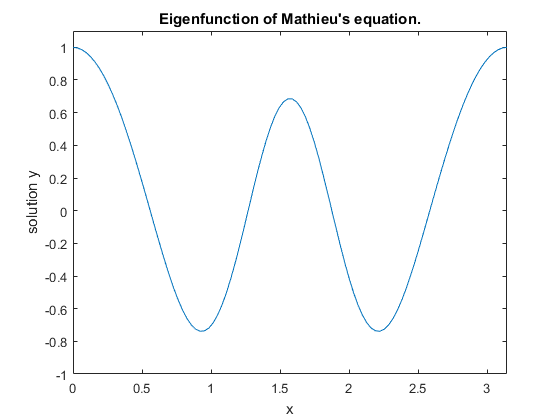
title('Eigenfunction of Mathieu''s equation.') 
xlabel('x')
ylabel('solution y')
% ------------------------------------------------------------
function dydx = mat4ode(x,y,lambda)
q = 5;
dydx = [  y(2)
         -(lambda - 2*q*cos(2*x))*y(1) ];
% ------------------------------------------------------------
function res = mat4bc(ya,yb,lambda)
res = [  ya(2) 
         yb(2) 
        ya(1)-1 ];
% ------------------------------------------------------------
function yinit = mat4init(x)
yinit = [  cos(4*x)
          -4*sin(4*x) ];

Дифференциальное уравнение (преобразованный в систему первого порядка) и граничные условия закодировано как локальные функции mat4ode и mat4bc, соответственно. Поскольку неизвестные параметры присутствуют, эти функции должны принять три входных параметра, даже при том, что некоторые аргументы не используются.

Структура предположения solinit формируется с bvpinit. Исходное предположение для решения предоставляется в форме функционального mat4init. Мы выбрали y =, потому что 4x, потому что он удовлетворяет граничные условия и имеет правильное качественное поведение (правильное количество изменений знака). В вызове bvpinit третий аргумент (lambda = 15) обеспечивает исходное предположение для неизвестного параметра λ.

После того, как проблема решена с bvp4c, поле sol.parameters возвращает значение λ = 17.097, и график показывает собственную функцию, сопоставленную с этим собственным значением.

Алгоритмы

bvp4c является кодом конечной разности, который реализует трехэтапную формулу Lobatto IIIa. Это - формула словосочетания, и многочлен словосочетания предоставляет решение ^{C1-continuous}, которое является четвертым порядком, точным однородно в [a,b]. Поймайте в сети выбор, и контроль ошибок основаны на невязке непрерывного решения.

Ссылки

[1] Шемпин, L.F., M.W. Reichelt, и Дж. Кирженка, “Решая Краевые задачи для Обыкновенных дифференциальных уравнений в MATLAB с bvp4c”

Документация