Извлеките и создайте разреженную полосу и диагональные матрицы
B = spdiags (A)
[B, d] = spdiags (A)
B = spdiags (A, d)
A = spdiags (B, d, A)
A = spdiags (B, d, m, n)
Функция spdiags обобщает функциональный diag. Четыре различных операции, которые отличает количество входных параметров, возможны.
B = spdiags(A) извлекает все ненулевые диагонали от m-by-n матричный A. B является min(m,n)-by-p матрица, столбцами которой является p ненулевые диагонали A.
[B,d] = spdiags(A) возвращает векторный d длины p, целочисленные компоненты которого задают диагонали в A.
B = spdiags(A,d) извлекает диагонали, заданные d.
A = spdiags(B,d,A) заменяет диагонали, заданные d со столбцами B. Вывод разрежен.
A = spdiags(B,d,m,n) создает m-by-n разреженная матрица путем взятия столбцов B и размещения их по диагоналям, заданным d.
В этом синтаксисе, если столбец B более длинен, чем диагональ, это заменяет, и m >= n, spdiags берет элементы супердиагоналей от более низкой части столбца B и элементы поддиагоналей от верхней части столбца B. Однако, если m < n, то супердиагонали от верхней части столбца B и поддиагоналей от более низкой части. (См. Пример 5 А и Пример 5B, ниже).
Функция spdiags имеет дело с тремя матрицами, в различных комбинациях, как оба ввода и вывода.
A |
|
B |
|
d | Вектор длины |
Примерно, A, B и d связаны
for k = 1:p
B(:,k) = diag(A,d(k))
endНекоторые элементы B, соответствуя положениям за пределами A, не заданы этими циклами. На них не ссылаются, когда B вводится и обнуляется, когда B выводится.
Матрица m на n A имеет m+n-1diagonals. Они заданы в векторном d с помощью индексов от-m+1 до n-1. Например, если A 5 6, он имеет 10 диагоналей, которые заданы в векторном d с помощью индексов-4,-3... 4, 5. Следующая схема иллюстрирует это для вектора из всех единиц.
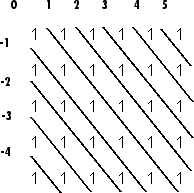
Для следующей матрицы,
A=[0 5 0 10 0 0;...
0 0 6 0 11 0;...
3 0 0 7 0 12;...
1 4 0 0 8 0;...
0 2 5 0 0 9]
A =
0 5 0 10 0 0
0 0 6 0 11 0
3 0 0 7 0 12
1 4 0 0 8 0
0 2 5 0 0 9команда
[B, d] =spdiags(A)
возвращается
B =
0 0 5 10
0 0 6 11
0 3 7 12
1 4 8 0
2 5 9 0
d =
-3
-2
1
3Столбцы первого вывода B содержат ненулевые диагонали A. Второй вывод d перечисляет индексы ненулевых диагоналей A, как показано в следующей схеме. Смотрите, Как Диагонали A Перечислены в Векторе d.
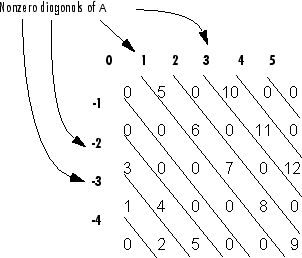
Обратите внимание на то, что самая длинная ненулевая диагональ в A содержится в столбце 3 B. Другим ненулевым диагоналям A добавили дополнительные нули к их соответствующим столбцам в B, чтобы дать все столбцы B та же длина. Для ненулевых диагоналей ниже основной диагонали A дополнительные нули добавляются в верхних частях столбцов. Для ненулевых диагоналей выше основной диагонали A дополнительные нули добавляются в нижних частях столбцов. Это проиллюстрировано следующей схемой.
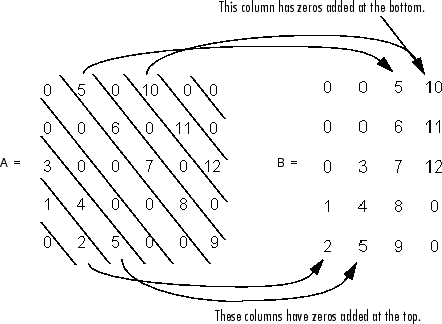
Этот пример генерирует разреженное трехдиагональное представление классического второго оператора различия на точках n.
e = ones(n,1); A = spdiags([e -2*e e], -1:1, n, n)
Превратите его в тестовую матрицу Уилкинсона (см. gallery):
A = spdiags(abs(-(n-1)/2:(n-1)/2)',0,A)
Наконец, восстановите эти три диагонали:
B = spdiags(A)
Второй пример не является квадратным.
A = [11 0 13 0
0 22 0 24
0 0 33 0
41 0 0 44
0 52 0 0
0 0 63 0
0 0 0 74]Здесь m =7, n = 4 и p = 3.
Оператор [B,d] = spdiags(A) производит d = [-3 0 2]' и
B = [41 11 0
52 22 0
63 33 13
74 44 24]С другой стороны, с вышеупомянутым B и d, выражением spdiags(B,d,7,4) воспроизводит исходный A.
Этот пример показывает, как spdiags создает диагонали, когда столбцы B более длинны, чем диагонали, они заменяют.
B = repmat((1:6)',[1 7])
B =
1 1 1 1 1 1 1
2 2 2 2 2 2 2
3 3 3 3 3 3 3
4 4 4 4 4 4 4
5 5 5 5 5 5 5
6 6 6 6 6 6 6
d = [-4 -2 -1 0 3 4 5];
A = spdiags(B,d,6,6);
full(A)
ans =
1 0 0 4 5 6
1 2 0 0 5 6
1 2 3 0 0 6
0 2 3 4 0 0
1 0 3 4 5 0
0 2 0 4 5 6Этот пример иллюстрирует использование синтаксиса A = spdiags(B,d,m,n) при трех условиях:
m равен n
m больше, чем n
m является меньше, чем n
Команда, используемая в этом примере,
A = full(spdiags(B, [-2 0 2], m, n))
где B 5 3 матрица, показанная ниже. Получившийся матричный A имеет размерности m-by-n и имеет ненулевые диагонали в [-2 0 2] (поддиагональ в -2, основная диагональ и супердиагональ в 2).
B = [1 6 11
2 7 12
3 8 13
4 9 14
5 10 15]Первые и третьи столбцы матричного B используются, чтобы создать под - и супердиагонали A соответственно. Во всех трех случаях, хотя, эти два внешних столбца B более длинны, чем получившиеся диагонали A. Из-за этого только часть столбцов используется в A.
Когда m == n или m > n, spdiags берет элементы супердиагонали в A от более низкой части соответствующего столбца B и элементы поддиагонали в A от верхней части соответствующего столбца B.
A = full(spdiags(B, [-2 0 2], 5, 5)) Matrix B Matrix A 1 6 11 6 0 13 0 0 2 7 12 0 7 0 14 0 3 8 13 == spdiags => 1 0 8 0 15 4 9 14 0 2 0 9 0 5 10 15 0 0 3 0 10
A(3,1), A(4,2) и A(5,3) взяты от верхней части B(:,1).
A(1,3), A(2,4) и A(3,5) взяты от более низкой части B(:,3).
A = full(spdiags(B, [-2 0 2], 5, 4)) Matrix B Matrix A 1 6 11 6 0 13 0 2 7 12 0 7 0 14 3 8 13 == spdiags => 1 0 8 0 4 9 14 0 2 0 9 5 10 15 0 0 3 0
То же самое как частично A.
Когда m < n, spdiags делает противоположное, беря элементы супердиагонали в A от верхней части соответствующего столбца B и элементы поддиагонали в A от более низкой части соответствующего столбца B.
A = full(spdiags(B, [-2 0 2], 4, 5)) Matrix B Matrix A 1 6 11 6 0 11 0 0 2 7 12 0 7 0 12 0 3 8 13 == spdiags => 3 0 8 0 13 4 9 14 0 4 0 9 0 5 10 15
A(3,1) и A(4,2) взяты от более низкой части B(:,1).
A(1,3), A(2,4) и A(3,5) взяты от верхней части B(:,3).
Извлеките диагонали от первой части этого примера назад в формат столбца с помощью команды
B = spdiags(A)
Вы видите, что в каждом случае первоначальные столбцы восстанавливаются (минус те элементы, которые переполнились супер - и поддиагонали матричного A).
Matrix A Matrix B 6 0 13 0 0 1 6 0 0 7 0 14 0 2 7 0 1 0 8 0 15 == spdiags => 3 8 13 0 2 0 9 0 0 9 14 0 0 3 0 10 0 10 15
Matrix A Matrix B 6 0 13 0 1 6 0 0 7 0 14 2 7 0 1 0 8 0 == spdiags => 3 8 13 0 2 0 9 0 9 14 0 0 3 0
Matrix A Matrix B 6 0 11 0 0 0 6 11 0 7 0 12 0 0 7 12 3 0 8 0 13 == spdiags => 3 8 13 0 4 0 9 0 4 9 0