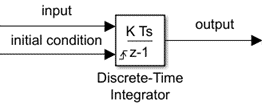
Интегратор дискретного времени

Выполните интегрирование дискретного времени или накопление сигнала

Библиотека:
Simulink / Обычно Используемые Блоки
Simulink / Дискретный

Описание

Используйте блок Discrete-Time Integrator вместо блока Integrator, чтобы создать чисто дискретную модель. С блоком Discrete-Time Integrator вы можете:

Задайте начальные условия на блочном диалоговом окне или, как введено к блоку
Задайте входное усиление (K) значение
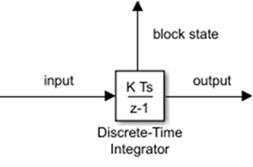
Выведите блочное состояние
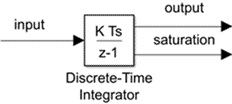
Задайте верхний и нижние пределы на интеграле
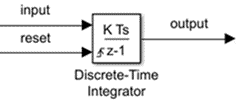
Сбросьте состояние с дополнительным входным параметром сброса

Выведите уравнения

С первым временным шагом блок утверждает n = 0, или с начальным выводом y(0) = IC или с начальным состоянием x(0) = IC, в зависимости от Начального условия, устанавливающего значение параметров.

Для данного шага n > 0 со временем симуляции t(n) ^Simulink® обновляет вывод y(n) можно следующим образом:

Прямой Метод Эйлера:

y(n) = y(n-1) + K*[t(n) - t(n-1)]*u(n-1)

Обратный Метод Эйлера:
```
y(n) = y(n-1) + K*[t(n) - t(n-1)]*u(n)
```

Трапециевидный метод:

y(n) = y(n-1) + K*[t(n)-t(n-1)]*[u(n)+u(n-1)]/2

Simulink автоматически выбирает реализацию пространства состояний этих выходных уравнений в зависимости от блочной частоты дискретизации, которая может быть явной или инициирована. При использовании явной частоты дискретизации t(n)-t(n-1) уменьшает до частоты дискретизации T для всего n > 0.

Интегрирование и методы накопления

Этот блок может интегрировать или накопить сигнал с помощью прямого Эйлера, обратного Эйлера, или трапециевидного метода. Примите, что u является входным параметром, y является вывод, и x является состоянием. Для данного шага n Simulink обновляет y(n) и x(n+1). В режиме интеграции T является блочной частотой дискретизации (дельта T в случае инициированной частоты дискретизации). В режиме накопления, T = 1. Блочная частота дискретизации определяет, когда вывод вычисляется, но не выходное значение. K является значением усиления. Значения отсекают согласно верхнему или нижним пределам.

Передайте метод Эйлера

Передайте Метод Эйлера (значение по умолчанию), также известное как прямое прямоугольное, или левое приближение

Программное обеспечение аппроксимирует 1/s как T/(z-1). Выражения для вывода блока на шаге n:

x(n+1) = x(n) + K*T*u(n)
y(n)   = x(n)

Блок использует эти шаги, чтобы вычислить вывод:

Step 0:          y(0)   = IC (clip if necessary)
                 x(1)   = y(0) + K*T*u(0)

Step 1:          y(1)   = x(1)
                 x(2)   = x(1) + K*T*u(1)

Step n:          y(n)   = x(n)
                 x(n+1) = x(n) + K*T*u(n) (clip if necessary)

Используя этот метод, входной порт 1 не имеет прямого сквозного соединения.

Обратный метод Эйлера

Обратный Метод Эйлера, также известный как обратное прямоугольное или правое приближение

Программное обеспечение аппроксимирует 1/s как T*z/(z-1). Получившееся выражение для вывода блока на шаге n

y(n) = y(n-1) + K*T*u(n).

Позвольте x(n) = y((n)-1). Блок использует эти шаги, чтобы вычислить вывод.

Если установка условия Начальной буквы параметра установлена в Output или Auto для инициированного и подсистем вызова функций:
```
Step 0:          y(0) = IC (clipped if necessary)
                 x(1) = y(0)
```

Если установка условия Начальной буквы параметра установлена в Auto для неинициированных подсистем:

Step 0:          x(0)   = IC (clipped if necessary)
                 x(1)   = y(0) = x(0) + K*T*u(0)

Step 1:          y(1)   = x(1) + K*T*u(1)
                 x(2)   = y(1)

Step n:          y(n)   = x(n) + K*T*u(n)
                 x(n+1) = y(n)

Используя этот метод, входной порт 1 имеет прямое сквозное соединение.

Трапециевидный метод

Для этого метода программное обеспечение аппроксимирует 1/s как T/2*(z+1)/(z-1).

Когда T фиксируется (равный периоду выборки), выражения, чтобы вычислить вывод:

x(n) = y(n-1) + K*T/2*u(n-1)
y(n) = x(n) + K*T/2*u(n)

Если установка условия Начальной буквы параметра установлена в Output или Auto для инициированного и подсистем вызова функций:
```
Step 0:          y(0)   = IC (clipped if necessary)
                 x(1)   = y(0) + K*T/2*u(0)
```

Если установка условия Начальной буквы параметра установлена в Auto для неинициированных подсистем:

Step 0:          x(0)   = IC (clipped if necessary)
                 y(0)   = x(0) + K*T/2*u(0)
                 x(1)   = y(0) + K*T/2*u(0)

Step 1:          y(1)   = x(1) + K*T/2*u(1)
                 x(2)   = y(1) + K*T/2*u(1)

Step n:          y(n)   = x(n) + K*T/2*u(n)
                 x(n+1) = y(n) + K*T/2*u(n)

Здесь, x(n+1) является наилучшей оценкой следующего вывода. Это не то же самое как состояние, в том, что x(n) не равен y(n).

Используя этот метод, входной порт 1 имеет прямое сквозное соединение.

Когда T является Переменная

WhenT является переменной (например, полученный со времен инициирования), блок использует эти шаги, чтобы вычислить вывод.

Если установка условия Начальной буквы параметра установлена в Output или Auto для инициированного и подсистем вызова функций:
```
Step 0:          y(0)   = IC (clipped if necessary)
                 x(1)   = y(0)
```

Если установка условия Начальной буквы параметра установлена в Auto для неинициированных подсистем:

Step 0:          x(0)   = IC (clipped if necessary)
                 x(1)   = y(0) = x(0) + K*T/2*u(0)

Step 1:          y(1)   = x(1) + T/2*(u(1) + u(0))
                 x(2)   = y(1)

Step n:          y(n)   = x(n) + T/2*(u(n) + u(n-1))
                 x(n+1) = y(n)

Задайте начальные условия

Можно задать начальные условия в качестве параметра на блочном диалоговом окне или ввести их от внешнего сигнала:

Чтобы задать начальные условия как блочный параметр, установите Начальный исходный параметр условия на internal и введите значение в Начальное текстовое поле условия.
Чтобы обеспечить начальные условия из внешнего источника, установите Начальный исходный параметр условия на external. Дополнительный входной порт появляется на блоке.

Когда использовать порт состояния

Используйте порт состояния вместо выходного порта:

Когда вывод блока возвращен в блок через порт сброса или начальный порт условия, вызвав алгебраический цикл. Для примера смотрите модель sldemo_bounce_two_integrators.
Когда это необходимо, чтобы передать состояние от одной условно выполняемой подсистемы до другого, который может вызвать проблемы синхронизации. Для примера смотрите модель sldemo_clutch.

Можно работать вокруг этих проблем путем передачи состояния через порт состояния, а не выходной порт. Simulink генерирует состояние в немного отличающееся время от вывода, который защищает вашу модель от этих проблем. Чтобы вывести блочное состояние, установите флажок порта Состояния показа. Порт состояния появляется на верхней части блока.

Ограничьте интеграл

Чтобы сохранить вывод в определенных уровнях, выберите Limit флажок вывода и введите пределы в соответствующее текстовое поле. Выполнение так заставляет блок функционировать как ограниченный интегратор. Когда вывод достигает пределов, интегральное действие выключает, чтобы предотвратить интегральное завершение. Во время моделирования можно изменить пределы, но вы не можете измениться, ограничивается ли вывод. Таблица показывает, как блок определяет вывод.

Интеграл	Вывод
Меньше чем или равный Более низкому пределу насыщенности и входному параметру отрицательно	Сохраненный в Более низком пределе насыщенности
Между Более низким пределом насыщенности и Верхним пределом насыщенности	Интеграл
Больше, чем или равный Верхнему пределу насыщенности и входному параметру положительно	Сохраненный в Верхнем пределе насыщенности

Чтобы сгенерировать сигнал, который указывает, когда состояние ограничивается, установите флажок порта насыщенности Show. Новый порт насыщенности появляется ниже блочного выходного порта.

Сигнал насыщенности имеет одно из трех значений:

1 указывает, что верхний предел применяется.
0 указывает, что интеграл не ограничивается.
- 1 указывает, что нижний предел применяется.

Сбросьте состояние

Блок сбрасывает свое состояние к заданному начальному условию, на основе внешнего сигнала. Чтобы заставить блок сбрасывать свое состояние, выберите одну из Внешних опций параметра сброса. Порт сброса появляется, который указывает на триггерный тип сброса.

Порт сброса имеет прямое сквозное соединение. Если блок вывод возвращается в этот порт, или непосредственно или через серию блоков с прямым сквозным соединением, алгебраический цикл заканчивается. Чтобы разрешить этот цикл, подайте вывод блочного порта состояния в порт сброса вместо этого. Чтобы получить доступ к блочному состоянию, установите флажок порта Состояния показа.

Сбросьте триггерные типы

Внешний параметр сброса позволяет вам решить, что атрибут сброса сигнализирует, что инициировал сброс. Триггерные опции включают:

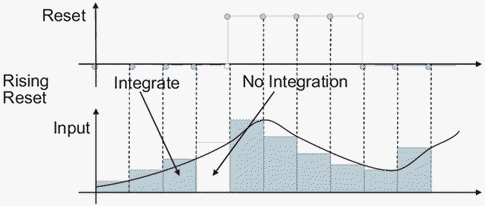
rising – Сбрасывает состояние, когда сигнал сброса имеет возрастающий край. Например, эти данные показывают эффект, что триггер сброса повышения имеет на обратном Эйлеровом интегрировании.
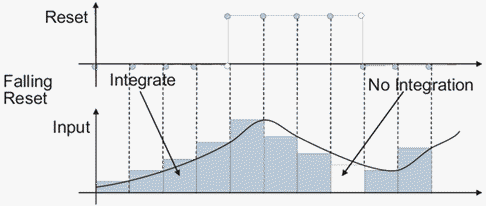
falling — Сбрасывает состояние, когда сигнал сброса имеет падающий край. Например, эти данные показывают эффект, что триггер сброса падения имеет на обратном Эйлеровом интегрировании.
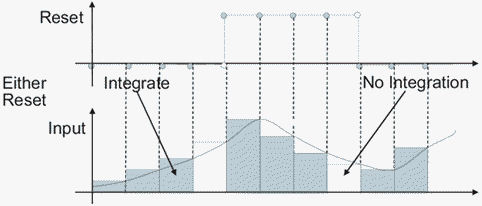
either — Сбрасывает состояние, когда сброс сигнализирует о повышениях или падениях. Например, следующие данные показывают эффект, что любой триггер сброса имеет на обратном Эйлеровом интегрировании.
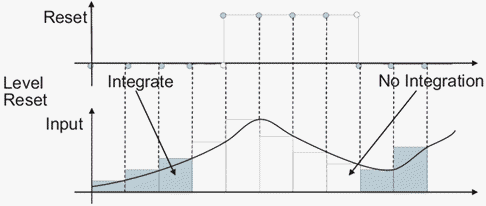
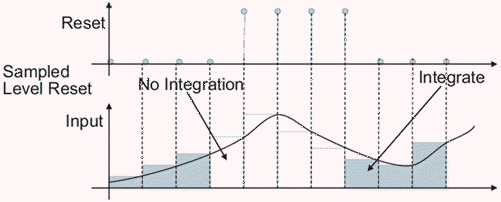
level — Сброс и содержит вывод к начальному условию, в то время как сигнал сброса является ненулевым. Например, эти данные показывают эффект, что триггер сброса уровня имеет на обратном Эйлеровом интегрировании.
sampled level — Сбрасывает вывод к начальному условию, когда сигнал сброса является ненулевым. Например, эти данные показывают эффект, что выбранный триггер сброса уровня имеет на обратном Эйлеровом интегрировании.

Опция сброса sampled level требует меньшего количества вычислений, делая его более эффективным, чем опция сброса level.
Примечание
Для блока Discrete-Time Integrator все триггерные обнаружения основаны на сигналах с положительными значениями. Например, сигнал, изменяющийся от-1 до 0, не рассматривается возрастающим краем, но сигнал, изменяющийся от 0 до 1.

Поведение в упрощенном режиме инициализации

Упрощенный режим инициализации включен, когда вы устанавливаете обнаружение инициализации Underspecified на Simplified в диалоговом окне Configuration Parameters. При использовании упрощенный режим инициализации, поведение блока Discrete-Time Integrator отличается от классического режима инициализации. Новое поведение инициализации более устойчиво и обеспечивает более сопоставимое поведение в этих случаях:

В алгебраических циклах
На включают и отключают
При сравнении результатов с помощью инициированной частоты дискретизации против явной частоты дискретизации, где блок инициирован на том же уровне как явная частота дискретизации

Упрощенный режим инициализации включает более легкое преобразование от Непрерывно-разовых блоков Интегратора до блоков Интегратора Дискретного времени, потому что начальные условия имеют то же значение для обоих блоков.

Для получения дополнительной информации о классических и упрощенных режимах инициализации смотрите обнаружение инициализации Underspecified.

Включите и Отключите Поведение с Начальным набором Установки Условия, чтобы Вывести

То, когда вы используете упрощенный режим инициализации с Начальным набором установки условия к Output для инициированного и подсистем вызова функций, разрешения и отключаете поведение блока, упрощено можно следующим образом.

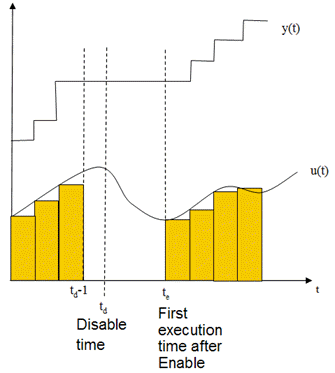
В отключают время _td:

 y(t_d) = y(t_d-1)

Во включают времени _te:

Если родительский порт управления подсистемы имеет состояния когда набор включения к reset:
```
y(t_e) = IC.
```
Если родительский порт управления подсистемы имеет состояния когда набор включения к held:
```
y(t_e) = y(t_d).
```
Следующие данные показывают это условие.

Подсистемы итератора

При использовании упрощенного режима инициализации вы не можете поместить блок Discrete-Time Integrator в блок подсистемы итератора.

В упрощенном режиме инициализации подсистемы Итератора не поддерживают прошедшее время. Таким образом, если блок Discrete-Time Integrator, которому требуется прошедшее время, помещается в блоке подсистемы итератора, Симулинк сообщает об ошибке.

Поведение в Enabled подсистеме в подсистеме вызова функций

Предположим, что у вас есть подсистема вызова функций, которая включает активированную подсистему, которая содержит блок Discrete-Time Integrator. Следующее поведение применяется.

Метод интегратора	Тип частоты дискретизации триггерного порта вызова функции	Значение `delta T`, когда подсистема вызова функций выполняется впервые после Enabled	Причина поведения
Передайте Эйлеру	Инициированный	`t — tstart`	Когда подсистема вызова функций выполняется впервые, алгоритм интегратора использует `tstart` в качестве предыдущего времени симуляции.
Обратный Эйлер и трапециевидный	Инициированный	`t — tprevious`	Когда подсистема вызова функций выполняется впервые, алгоритм интегратора использует `tprevious` в качестве предыдущего времени симуляции.
Передайте Эйлеру, обратному Эйлеру, и трапециевидный	Периодический	Частота дискретизации генератора вызова функции	В периодическом режиме блок Discrete-Time Integrator использует частоту дискретизации генератора вызова функции для `delta T`.

Порты

Входной параметр

развернуть все

`Port_1` — Входной сигнал
скаляр | вектор | матрица

Входной сигнал, заданный как скаляр, вектор или матрица

`Ic` Начальные условия состояний
скаляр | вектор | матрица

Начальные условия состояний, заданных как конечный скаляр, вектор или матрица.

Зависимости

Чтобы включить этот порт, установите Начальный источник условия на external.

Вывод

развернуть все

`Port_1` — Интегрирование дискретного времени или накопление входного параметра
скаляр | вектор | матрица

Интегрирование дискретного времени или накопление входного сигнала, заданного как скаляр, вектор или матрица.

`Port_2` — Saturation вывод
скаляр | вектор | матрица

Сигнал, указывающий, когда состояние ограничивается, задал как скаляр, вектор или матрица. Сигнал имеет одно из трех значений:

1 указывает, что верхний предел применяется.
0 указывает, что интеграл не ограничивается.
-1 указывает, что нижний предел применяется.

Зависимости

Чтобы включить этот порт, установите флажок порта насыщенности Show.

Типы данных: единственный | удваиваются | int8

`Port_3` — State вывод
скаляр | вектор | матрица

Блокируйте состояния, выведите как скаляр, вектор или матрица. По умолчанию блок добавляет этот порт к верхней части блочного значка. Используйте порт состояния когда:

Вывод блока возвращен в блок через порт сброса или начальный порт условия, вызвав алгебраический цикл. Для примера смотрите модель sldemo_bounce_two_integrators.
Вы хотите передать состояние от одной условно выполняемой подсистемы до другого, который может вызвать проблемы синхронизации. Для примера смотрите модель sldemo_clutch.

Для получения дополнительной информации смотрите, Когда Использовать Порт состояния.

Зависимости

Чтобы включить этот порт, установите флажок порта Состояния показа.

Параметры

развернуть все

Основной

`Integrator method` — Метод накопления
`Integration: Forward Euler` (значение по умолчанию) | `Integration: Backward Euler` | `Integration: Trapezoidal` | `Accumulation: Forward Euler` | `Accumulation: Backward Euler` | `Accumulation: Trapezoidal`

Задайте метод интегрирования или накопления. Смотрите Выходные Уравнения и Методы Интегрирования и Накопления для получения дополнительной информации.

Программируемое использование

Блочный параметр: IntegratorMethod

Ввод: символьный вектор

Значение по умолчанию: 'Integration: Forward Euler'

`Gain value` — Значение, чтобы умножиться с входным параметром интегратора
`1.0` (значение по умолчанию) | скаляр | вектор

Задайте скаляр, вектор или матрицу, на которую можно умножить входной параметр интегратора. Каждый элемент усиления должен быть положительным вещественным числом.

Определение значения кроме 1,0 (значение по умолчанию) семантически эквивалентно соединению блока Gain к входному параметру интегратора.
Действительные доступы включают:
- double(1.0)
- single(1.0)
- [1.1 2.2 3.3 4.4]
- [1.1 2.2; 3.3 4.4]

Совет

Используя этот параметр, чтобы задать входное усиление устраняет операцию умножения в сгенерированном коде. Однако этот параметр должен быть ненастраиваемым, чтобы понять это преимущество. Если вы хотите настроить входное усиление, установите этот параметр на 1,0 и используйте внешний блок Gain, чтобы задать входное усиление.

Программируемое использование

Блочный параметр: gainval

Ввод: символьный вектор

Значения: скаляр | вектор

Значение по умолчанию: '1.0'

`External reset` — Выберите, когда сбросить состояния к начальным условиям
`none` (значение по умолчанию) | `rising` | `falling` | `either` | `level` | `sampled level`

Выберите тип триггерного события, которое сбрасывает состояния к их начальным условиям:

'none' Не сбрасывайте состояние к начальным условиям.
rising — Сбросьте состояние, когда сигнал сброса будет иметь возрастающий край.
falling — Сбросьте состояние, когда сигнал сброса будет иметь падающий край.
either — Сбросьте состояние, когда сброс будет сигнализировать о повышениях или падениях.
level — Сбросьте и содержите вывод к начальному условию, в то время как сигнал сброса является ненулевым.
sampled level — Сбросьте вывод к начальному условию, когда сигнал сброса будет ненулевым.

Для получения дополнительной информации смотрите Сброс состояние и Триггерные Типы Сброса.

Программируемое использование

Блочный параметр: ExternalReset

Ввод: символьный вектор

Значение по умолчанию: 'none'

`Initial condition source` — Выберите источник начального условия
`internal` (значение по умолчанию) | `external`

Выберите источник начального условия:

internal — Получите начальные условия состояний от Начального блочного параметра условия.
external — Получите начальные условия состояний от внешнего блока через входной порт IC.

Зависимости

Выбор internal включает Начальный параметр условия.

Выбор external отключает Начальный параметр условия и включает входной порт IC.

Программируемое использование

Блочный параметр: InitialConditionSource

Ввод: вектор символа, строка

Значения: 'внутренний' | 'внешний'

Значение по умолчанию: 'internal'

`Initial condition` — Начальное условие состояний
`0` (значение по умолчанию) | скаляр | вектор | матрица

Задайте начальное условие блочных состояний. Минимальные и максимальные значения связаны Выходным минимумом и Выходными блочными параметрами максимума.

Совет

Программное обеспечение Simulink не позволяет начальному условию этого блока быть inf или NaN.

Зависимости

Чтобы включить этот параметр, установите Начальный источник условия на internal.

Программируемое использование

Блочный параметр: InitialCondition

Ввод: вектор символа, строка

Значения: скаляр | вектор | матрица

Значение по умолчанию: '0'

`Initial condition setting` — Выберите, где применить начальное условие
`Auto` (значение по умолчанию) | `Output` | `Compatibility`

Выберите, применить ли значение Начального параметра условия к блочному состоянию или блоку вывод. Начальное условие является также значением сброса.

'auto' Блок выбирает, где применить Начальный параметр условия.
- Если блок находится в неинициированной подсистеме, и метод Интегратора установлен в метод интегрирования, установите начальные условия:
  x(0) = IC
  В сбросе:
  x(n) = IC
- Если блок находится в инициированном или подсистеме вызова функций, и метод Интегратора установлен в метод интегрирования, установите начальные условия, как будто output был выбран.
Вывод Используйте эту опцию, когда блок находится в инициированном или подсистеме вызова функций, и метод Интегратора установлен в метод интегрирования.
Установленные начальные условия:
y(0) = IC
В сбросе:
y(n) = IC
Compatibility — Эта опция присутствует, чтобы обеспечить обратную совместимость. Вы не можете выбрать эту опцию для блоков Интегратора Дискретного времени в моделях Simulink, но можно выбрать ее для блоков Интегратора Дискретного времени в библиотеке. Используйте эту опцию, чтобы поддержать совместимость с моделями Simulink, созданными перед R2014a.
До R2014a опция Auto был известен как State only (most efficient). Опция Output была известна как State and output. Поведение блока с опцией Compatibility следующие.
- Если обнаружение инициализации Underspecified установлено в Classic, Начальный параметр установки условия ведет себя как Auto.
- Если обнаружение инициализации Underspecified установлено в Simplified, Начальный параметр установки условия ведет себя как Output.

Примечание

Этот параметр назвали условием начальной буквы Использования как начальный и значение сброса для в Simulink перед R2014a.

Программируемое использование

Блочный параметр: InitialConditionSetting

Ввод: символьный вектор

Значение: 'Auto' | 'Вывод' | 'Совместимость'

Значение по умолчанию: 'auto'

`Sample time (-1 for inherited)` — Интервал между выборками
`-1` (значение по умолчанию) | скаляр | вектор

Введите интервал дискретного времени между шагами.

По умолчанию блок использует дискретную частоту дискретизации 1. Чтобы назначить различное время дискретизации, введите другое дискретное значение, такой как 0,1.

См. Настройку времени выборки для получения дополнительной информации.

Советы

Не задавайте частоту дискретизации 0. Это значение задает время непрерывной выборки, которое не поддерживает блок Discrete-Time Integrator.
Не задавайте частоту дискретизации inf или NaN, потому что эти значения не дискретны.
Если вы задаете-1, чтобы наследовать частоту дискретизации от восходящего блока, проверить, что восходящий блок использует дискретную частоту дискретизации. Например, блок Discrete-Time Integrator не может наследовать частоту дискретизации 0.

Программируемое использование

Блочный параметр: 'SampleTime'

Ввод: символьный вектор

Значения: скаляр | вектор

Значение по умолчанию: '-1'

Выходные значения блока `Limit output` — Limit к заданной области значений
`off` (значение по умолчанию) | `on`

Ограничьте вывод блока значением между Более низким пределом насыщенности и Верхними предельными параметрами насыщенности.

Выбор этого флажка ограничивает вывод блока значением между Более низким пределом насыщенности и Верхними предельными параметрами насыщенности.
Снятие этого флажка не ограничивает выходные значения блока.

Нижнее значение выходной области значений это Simulink Check.

Симулинк использует минимум, чтобы выполнить:

Проверка диапазона параметра (см., Задает Минимальные и Максимальные значения для Блочных Параметров) для некоторых блоков.
Проверка диапазона моделирования (см. Диапазоны сигнала и Включают Проверку диапазона Моделирования).
Автоматическое масштабирование типов данных фиксированной точки.
Оптимизация кода, который вы генерируете от модели. Эта оптимизация может удалить алгоритмический код и влиять на результаты некоторых режимов моделирования, такие как SIL или режим external mode. Для получения дополнительной информации смотрите, Оптимизируют использование заданных минимальных и максимальных значений (Simulink Coder).

Примечание

Выведите минимум, не насыщает или отсекает фактический выходной сигнал. Используйте блок Saturation вместо этого.

Программируемое использование

Блочный параметр: OutMin

Ввод: символьный вектор

Значения:' []' | скаляр

Значение по умолчанию: '[ ]'

`Output maximum` — Максимальное выходное значение для проверки диапазона
`[]` (значение по умолчанию) | скаляр

Верхнее значение выходной области значений это Simulink Check.

Симулинк использует максимальное значение, чтобы выполнить:

Проверка диапазона параметра (см., Задает Минимальные и Максимальные значения для Блочных Параметров) для некоторых блоков.
Проверка диапазона моделирования (см. Диапазоны сигнала и Включают Проверку диапазона Моделирования).
Автоматическое масштабирование типов данных фиксированной точки.
Оптимизация кода, который вы генерируете от модели. Эта оптимизация может удалить алгоритмический код и влиять на результаты некоторых режимов моделирования, такие как SIL или режим external mode. Для получения дополнительной информации смотрите, Оптимизируют использование заданных минимальных и максимальных значений (Simulink Coder).

Примечание

Выведите максимум, не насыщает или отсекает фактический выходной сигнал. Используйте блок Saturation вместо этого.

Программируемое использование

Блочный параметр: OutMax

Ввод: символьный вектор

Значения:' []' | скаляр

Значение по умолчанию: '[ ]'

`Тип данных` Тип выходных данных
`Inherit: Inherit via internal rule` (значение по умолчанию) | `Inherit: Inherit via back propagation` | `double` | `single` | `int8` | `uint8` | `int16` | `uint16` | `int32` | `uint32` | `fixdt(1,16)` | `fixdt(1,16,0)` | `fixdt(1,16,2^0,0)` | `<data type expression>`

Выберите тип данных для вывода. Тип может быть наследован, задан непосредственно или выражен как объект типа данных, такой как Simulink.NumericType. Для получения дополнительной информации смотрите Типы данных Управляющего сигнала.

Когда вы выбираете наследованную опцию, блок ведет себя можно следующим образом:

Inherit: Inherit via internal rule — Симулинк выбирает тип данных, чтобы сбалансировать числовую точность, производительность и размер сгенерированного кода, при принятии во внимание свойств аппаратных средств целевого процессора. Если вы изменяете настройки целевого процессора, тип данных, выбранный внутренним правилом, может измениться. Например, если блок умножает входной параметр типа, int8 усилением int16 и ASIC/FPGA задан как целенаправленный тип оборудования, типом выходных данных является sfix24. Если Unspecified (assume 32-bit Generic), i. e., типичный 32-битный микропроцессор, задан как целевой компьютер, типом выходных данных является int32. Если ни один из размеров слова, обеспеченных целевым микропроцессором, не может разместить выходную область значений, программное обеспечение Симулинка отображает ошибку в Диагностическом Средстве просмотра.
Для программного обеспечения не всегда возможно оптимизировать эффективность кода и числовую точность в то же время. Если внутреннее правило не удовлетворяет ваши определенные потребности для числовой точности или производительности, используйте одну из следующих опций:
- Задайте тип выходных данных явным образом.
- Используйте простой выбор Inherit: Same as input.
- Явным образом задайте тип данных по умолчанию, такой как fixdt(1,32,16) и затем используйте Fixed-Point Tool, чтобы предложить типы данных для вашей модели. Для получения дополнительной информации смотрите fxptdlg.
- Чтобы задать ваше собственное правило наследования, используйте Inherit: Inherit via back propagation и затем используйте блок Data Type Propagation. Примеры того, как использовать этот блок, доступны в библиотеке Signal Attributes блок Data Type Propagation Examples.
Inherit: Inherit via back propagation — Используйте тип данных ведущего блока.

Программируемое использование

Блочный параметр: OutDataTypeStr

Ввод: символьный вектор

Значение по умолчанию: 'Inherit: Inherit via internal rule'

`Lock output data type setting against changes by the fixed-point tools` — Препятствуйте тому, чтобы Fixed-Point Tool заменили тип Выходных данных
`off` (значение по умолчанию) | `on`

Выберите этот параметр, чтобы препятствовать тому, чтобы Fixed-Point Tool заменили тип Выходных данных, который вы задаете на блоке. Для получения дополнительной информации смотрите, что Тип Выходных данных Блокировки Использования Устанавливает (Fixed-Point Designer).

Программируемое использование

Блочный параметр: LockScale

Ввод: символьный вектор

Значения: 'off' | 'on'

Значение по умолчанию: 'off'

`Integer rounding mode` — Задайте округляющийся режим для операций фиксированной точки
`Floor` (значение по умолчанию) | `Ceiling` | `Convergent` | `Nearest` | `Round` | `Simplest` | `Zero`

Выберите один из этих режимов округления.

Ceiling: Раунды и положительные и отрицательные числа к положительной бесконечности. Эквивалентный функции ^MATLAB®ceil.
Convergent: Номер раундов к самому близкому представимому значению. Если связь происходит, раунды к самому близкому даже целое число. Эквивалентный Фиксированной точке Designer™ функция convergent.
Пол: Раунды и положительные и отрицательные числа к отрицательной бесконечности. Эквивалентный функции floor MATLAB.
Самый близкий: Номер раундов к самому близкому представимому значению. Если связь происходит, раунды к положительной бесконечности. Эквивалентный Fixed-Point Designer функция nearest.
Вокруг: Номер раундов к самому близкому представимому значению. Если связь происходит, округляет положительные числа к положительной бесконечности и округляет отрицательные числа к отрицательной бесконечности. Эквивалентный Fixed-Point Designer функция round.
Simplest: Автоматически выбирает между раундом к полу и вокруг к нулю, чтобы сгенерировать округление кода, который максимально эффективен.
Zero: Номер раундов к нулю. Эквивалентный функции fix MATLAB.

Программируемое использование

Блочный параметр: RndMeth

Ввод: символьный вектор

Значение по умолчанию: пол

Смотрите также

Для получения дополнительной информации смотрите Округление (Fixed-Point Designer).

`Saturate on integer overflow` — Метод действия переполнения
`off` (значение по умолчанию) | `on`

Задайте, насыщает ли переполнение или переносится.

'off' Переполнение переносится к соответствующему значению, которое может представлять тип данных.
Например, номер 130 не помещается в 8-битное целое число со знаком и переносится к-126.
on — Переполнение насыщает или к минимальному или к максимальному значению, которое может представлять тип данных.
Например, переполнение, сопоставленное с 8-битным целым числом со знаком, может насыщать к-128 или 127.

Совет

Рассмотрите установку этого флажка, когда ваша модель имеет возможное переполнение, и вы хотите явную защиту насыщенности в сгенерированном коде.
Полагайте, что снятие этого флажка когда это необходимо оптимизирует эффективность вашего сгенерированного кода.
Снятие этого флажка также помогает вам постараться не чрезмерно определять, как блок обрабатывает сигналы из области значений. Для получения дополнительной информации смотрите Проверку на Ошибки Диапазона сигнала.
Когда вы устанавливаете этот флажок, насыщенность применяется к каждой внутренней операции на блоке, не только выводу или результату.
В целом процесс генерации кода может обнаружить, когда переполнение не возможно. В этом случае генератор кода не производит код насыщенности.

Программируемое использование

Блочный параметр: SaturateOnIntegerOverflow

Ввод: символьный вектор

Значения: 'off' | 'on'

Значение по умолчанию: 'off'

Атрибуты состояния

`State name` — Уникальное имя для блочного состояния
`''` (значение по умолчанию) | алфавитно-цифровая строка

Используйте этот параметр, чтобы присвоить уникальное имя блочному состоянию. Значением по умолчанию является ' '. Когда это поле является пробелом, никакое имя не присвоено. При использовании этого параметра помните эти факторы:

Допустимый идентификатор запускается с буквенного символа или символа подчеркивания, сопровождаемого алфавитно-цифровыми символами или символами подчеркивания.
Имя состояния применяется только к выбранному блоку.

Для получения дополнительной информации смотрите, Применяют Классы памяти к Отдельному Сигналу, состоянию и Элементам данных Параметра (Simulink Coder).

Зависимости

То, когда вы задаете значение для имени состояния и нажимаете Apply, вы включаете имя состояния, должно решить к параметру объекта Сигнала Simulink.

Программируемое использование

Параметр: StateName

Ввод: символьный вектор

Значения: уникальное имя

Значение по умолчанию: ''

`State name must resolve to Simulink signal object` — Потребуйте, чтобы имена состояния разрешили сигнализировать об объекте
`Off` (значение по умолчанию) | булевская переменная

Задайте при требовании, чтобы имя состояния решило к объектам Сигнала Simulink или нет. Если выбрано, программное обеспечение генерирует ошибку во время выполнения, если вы задаете имя состояния, которое не совпадает с именем объекта Сигнала Simulink.

Зависимость

Enabled, когда вы даете состояние параметра, называют значение и устанавливают образцовое разрешение Сигнала параметра конфигурации значения кроме None.

Установка этого флажка отключает класс памяти Генерации кода.

Программируемое использование

Блочный параметр: StateMustResolveToSignalObject

Ввод: символьный вектор

Значения: 'off' | 'on'

Значение по умолчанию: 'off'

`Signal object class` — Пользовательское имя пакета класса памяти
`Simulink.Signal` (значение по умолчанию)

Выберите пользовательский пакет класса памяти путем выбора класса объекта сигнала, который задает целевой пакет. Например, чтобы применить пользовательские классы памяти от встроенного пакета mpt, выберите mpt.Signal. Если вы не используете основанную на ERT цель генерации кода со Встроенным ^Coder®, пользовательские классы памяти не влияют на сгенерированный код.

Если класс, который вы хотите, не появляется в списке, выберите Customize class lists. Для инструкций смотрите, что Целевой Класс Не Появляется в Списке Классов объектов Сигнала (Embedded Coder).

Для получения информации о классах памяти смотрите, Применяют Классы памяти к Отдельному Сигналу, состоянию и Элементам данных Параметра (Simulink Coder). Для получения информации о пользовательских классах памяти смотрите, Применяют Пользовательские Классы памяти к Отдельному Сигналу, состоянию и Элементам данных Параметра (Embedded Coder).

Программируемое использование

Блочный параметр: StateSignalObject

Ввод: символьный вектор

Значения: 'Simulink. Сигнал' |' <StorageClass. PackageName>'

Значение по умолчанию: 'Simulink.Signal'

`Code generation storage class` — Класс памяти для генерации кода
`Auto` (значение по умолчанию) | `Model default` | `ExportedGlobal` | `ImportedExtern` | `ImportedExternPointer` | `Bitfield (Custom)` | `Volatile (Custom)` | `ExportToFile (Custom)` | `ImportFromFile (Custom)` | `FileScope (Custom)` | `Struct (Custom)` | `GetSet (Custom)` | `Reusable (Custom)`

Выберите класс памяти состояния для генерации кода. Если вы не должны взаимодействовать через интерфейс к внешнему коду, выберите Auto.

Для получения дополнительной информации смотрите, Применяют Классы памяти к Отдельному Сигналу, состоянию и Элементам данных Параметра (Simulink Coder) и Применяют Пользовательские Классы памяти к Отдельному Сигналу, состоянию и Элементам данных Параметра (Embedded Coder).

Программируемое использование

Блочный параметр: StateStorageClass

Ввод: символьный вектор

Значение по умолчанию: 'auto'

`TypeQualifier` — Спецификатор типа хранения
`''` (значение по умолчанию) | `const` | `volatile` |...

Задайте спецификатор типа хранения, такой как const или volatile.

Примечание

TypeQualifier будет удален в будущем релизе. Чтобы применить спецификаторы типа хранения к данным, используйте разделы custom storage classes и memory. Если вы не используете основанную на ERT цель генерации кода с Embedded Coder, разделы custom storage classes и memory не влияют на сгенерированный код.

Зависимости

Чтобы включить этот параметр, установите класс памяти Генерации кода на ExportedGlobal, ImportedExtern, ImportedExternPointer или Model default. Этот параметр скрыт, если вы ранее не устанавливаете его значение.

Программируемое использование

Блочный параметр: RTWStateStorageTypeQualifier

Ввод: символьный вектор

Значения:'' | 'const' | 'энергозависимый' |...

Значение по умолчанию: ''

Образцовые примеры

Discrete-Time Integration Using the Forward Euler Integration Method

Интегрирование дискретного времени Используя прямой эйлеров метод интегрирования

sldemo_fuelsys модель использует блок Discrete-Time Integrator в fuel_rate_control/airflow_calc подсистеме.

Открытый пример

Создание модели тупика муфты

Этот пример показывает, как использовать Simulink®, чтобы смоделировать и моделировать систему муфты вращения. Несмотря на то, что моделирование системы муфты является трудным из-за топологических изменений в системной динамике во время тупика, этот пример показывает, как активированные подсистемы Симулинка легко решают такие проблемы. Мы иллюстрируем, как нанять важный Simulink, моделируя концепции в создании моделирования муфты. Разработчики могут применить эти концепции ко многим моделям с сильными разрывами и ограничениями, которые могут измениться динамически.

Открытая модель

Моделирование прыгающего мяча

Этот пример показывает, как использовать два разных подхода к моделированию прыгающего мяча с помощью Simulink®.

Открытая модель

Блокируйте характеристики

Типы данных	`double` \| `single` \| `base integer` \| `fixed point`
Прямое сквозное соединение	`Yes`
Многомерные сигналы	`No`
Сигналы переменного размера	`No`
Обнаружение пересечения нулем	`No`

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.

Зависит от абсолютного времени, когда используется в инициированной иерархии подсистемы.

Генерация HDL-кода
Сгенерируйте Verilog и код VHDL для FPGA и проектов ASIC с помощью HDL Coder™.

Для получения дополнительной информации о генерации HDL-кода, смотрите Интегратор Дискретного времени.

Документация

Интегратор дискретного времени

Описание

Выведите уравнения

Интегрирование и методы накопления

Передайте метод Эйлера

Обратный метод Эйлера

Трапециевидный метод

Когда T является Переменная

Задайте начальные условия

Когда использовать порт состояния

Ограничьте интеграл

Сбросьте состояние

Сбросьте триггерные типы

Примечание

Поведение в упрощенном режиме инициализации

Включите и Отключите Поведение с Начальным набором Установки Условия, чтобы Вывести

Подсистемы итератора

Поведение в Enabled подсистеме в подсистеме вызова функций

Порты

Входной параметр

Port_1 — Входной сигнал скаляр | вектор | матрица

Ic Начальные условия состояний скаляр | вектор | матрица

Зависимости

Вывод

Port_1 — Интегрирование дискретного времени или накопление входного параметра скаляр | вектор | матрица

Port_2 — Saturation вывод скаляр | вектор | матрица

Зависимости

Port_3 — State вывод скаляр | вектор | матрица

Зависимости

Параметры

Основной

Integrator method — Метод накопления Integration: Forward Euler (значение по умолчанию) | Integration: Backward Euler | Integration: Trapezoidal | Accumulation: Forward Euler | Accumulation: Backward Euler | Accumulation: Trapezoidal

Программируемое использование

Gain value — Значение, чтобы умножиться с входным параметром интегратора 1.0 (значение по умолчанию) | скаляр | вектор

Совет

Программируемое использование

External reset — Выберите, когда сбросить состояния к начальным условиям none (значение по умолчанию) | rising | falling | either | level | sampled level

Программируемое использование

Initial condition source — Выберите источник начального условия internal (значение по умолчанию) | external

Зависимости

Программируемое использование

Initial condition — Начальное условие состояний 0 (значение по умолчанию) | скаляр | вектор | матрица

Совет

Зависимости

Программируемое использование

Initial condition setting — Выберите, где применить начальное условие Auto (значение по умолчанию) | Output | Compatibility

Примечание

Программируемое использование

Sample time (-1 for inherited) — Интервал между выборками -1 (значение по умолчанию) | скаляр | вектор

Советы

Программируемое использование

Выходные значения блока Limit output — Limit к заданной области значений off (значение по умолчанию) | on

Зависимости

Программируемое использование

Upper saturation limit — Верхний предел для интеграла inf (значение по умолчанию) | скаляр | вектор | матрица

Зависимости

Программируемое использование

Lower saturation limit — Нижний предел для интеграла -inf (значение по умолчанию) | скаляр | вектор | матрица

Зависимости

Программируемое использование

Show saturation port — Включите выходной порт насыщенности off (значение по умолчанию) | on

Зависимости

Программируемое использование

Show state port — Включите выходной порт состояния off (значение по умолчанию) | on

Зависимости

Программируемое использование

Блок Ignore limit and reset when linearizing — Treat как не восстановленный off (значение по умолчанию) | on

Совет

Программируемое использование

Атрибуты сигнала

Output minimum — Минимальное выходное значение для проверки диапазона [] (значение по умолчанию) | скаляр

Примечание

Программируемое использование

Output maximum — Максимальное выходное значение для проверки диапазона [] (значение по умолчанию) | скаляр

Примечание

Программируемое использование

Программируемое использование

Lock output data type setting against changes by the fixed-point tools — Препятствуйте тому, чтобы Fixed-Point Tool заменили тип Выходных данных off (значение по умолчанию) | on

Программируемое использование

`Port_1` — Входной сигнал
скаляр | вектор | матрица

`Ic` Начальные условия состояний
скаляр | вектор | матрица

`Port_1` — Интегрирование дискретного времени или накопление входного параметра
скаляр | вектор | матрица

`Port_2` — Saturation вывод
скаляр | вектор | матрица

`Port_3` — State вывод
скаляр | вектор | матрица

`Integrator method` — Метод накопления
`Integration: Forward Euler` (значение по умолчанию) | `Integration: Backward Euler` | `Integration: Trapezoidal` | `Accumulation: Forward Euler` | `Accumulation: Backward Euler` | `Accumulation: Trapezoidal`

`Gain value` — Значение, чтобы умножиться с входным параметром интегратора
`1.0` (значение по умолчанию) | скаляр | вектор

`External reset` — Выберите, когда сбросить состояния к начальным условиям
`none` (значение по умолчанию) | `rising` | `falling` | `either` | `level` | `sampled level`

`Initial condition source` — Выберите источник начального условия
`internal` (значение по умолчанию) | `external`

`Initial condition` — Начальное условие состояний
`0` (значение по умолчанию) | скаляр | вектор | матрица

`Initial condition setting` — Выберите, где применить начальное условие
`Auto` (значение по умолчанию) | `Output` | `Compatibility`

`Sample time (-1 for inherited)` — Интервал между выборками
`-1` (значение по умолчанию) | скаляр | вектор

Выходные значения блока `Limit output` — Limit к заданной области значений
`off` (значение по умолчанию) | `on`

`Upper saturation limit` — Верхний предел для интеграла
`inf` (значение по умолчанию) | скаляр | вектор | матрица

`Lower saturation limit` — Нижний предел для интеграла
`-inf` (значение по умолчанию) | скаляр | вектор | матрица

`Show saturation port` — Включите выходной порт насыщенности
`off` (значение по умолчанию) | `on`

`Show state port` — Включите выходной порт состояния
`off` (значение по умолчанию) | `on`

Блок `Ignore limit and reset when linearizing` — Treat как не восстановленный
`off` (значение по умолчанию) | `on`

`Output minimum` — Минимальное выходное значение для проверки диапазона
`[]` (значение по умолчанию) | скаляр

`Output maximum` — Максимальное выходное значение для проверки диапазона
`[]` (значение по умолчанию) | скаляр

`Lock output data type setting against changes by the fixed-point tools` — Препятствуйте тому, чтобы Fixed-Point Tool заменили тип Выходных данных
`off` (значение по умолчанию) | `on`

`Integer rounding mode` — Задайте округляющийся режим для операций фиксированной точки
`Floor` (значение по умолчанию) | `Ceiling` | `Convergent` | `Nearest` | `Round` | `Simplest` | `Zero`

`Saturate on integer overflow` — Метод действия переполнения
`off` (значение по умолчанию) | `on`

`State name` — Уникальное имя для блочного состояния
`''` (значение по умолчанию) | алфавитно-цифровая строка

`State name must resolve to Simulink signal object` — Потребуйте, чтобы имена состояния разрешили сигнализировать об объекте
`Off` (значение по умолчанию) | булевская переменная

`Signal object class` — Пользовательское имя пакета класса памяти
`Simulink.Signal` (значение по умолчанию)

`TypeQualifier` — Спецификатор типа хранения
`''` (значение по умолчанию) | `const` | `volatile` |...

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.

Генерация HDL-кода
Сгенерируйте Verilog и код VHDL для FPGA и проектов ASIC с помощью HDL Coder™.

Генерация кода PLC
Сгенерируйте код Структурированного текста с помощью Simulink® PLC Coder™.

Преобразование фиксированной точки
Преобразуйте алгоритмы с плавающей точкой в фиксированную точку с помощью Фиксированной точки Designer™.