Массивы Бога

Что такое массивы Бога?

Массивы Бога являются прямоугольными массивами бесконечной степени. В бесконечном массиве один элемент вызвал элементарную ячейку, повторяется однородно бесконечное число времен вдоль плоскости.

Анализ Бога массивов

Все массивы, используемые в реальных сценариях, конечны. Но антенные решетки, используемые в радио-астрономии, ПВО или радаре наблюдения, могут иметь больше чем 1 000 элементов антенны. В таких больших массивах электромагнитный анализ каждого элемента является утомительным и трудоемким.

Анализ Бога массивов игнорирует эффект усечения (краевой эффект) в ребрах массивов. Метод анализирует поведение активного элемента антенны как функция частоты и сканирования. Цель бесконечного анализа массивов состоит в том, чтобы извлечь поведение активного элемента антенны, встроенного в массив.

Предположения

Для бесконечного анализа массивов размер массивов должен быть больше, чем 10x10. Метод делает другие предположения:

Каждый элемент идентичен.
Каждый элемент однородно взволнован в амплитуде.
Все элементы расположены с интервалами однородно в двух измерениях.

Решатель Бога массивов

Чтобы смоделировать бесконечный массив, формулировка метода моментов (MoM) изменяется, чтобы составлять бесконечное поведение, заменяя функции Грина на периодические функции Грина. Периодическая функция Грина является бесконечным двойным суммированием.

Функция Грина	Периодическая функция Грина
$\begin{array}{l} g = \frac{e^{- j k R}}{R} \\ R = \| \vec{r} - {\vec{r}}^{'} \| \end{array}$	$\begin{array}{l} g_{периодический} = \sum_{m = - \infty}^{\infty} \sum_{n = - \infty}^{\infty} e^{j ϕ_{m n}} \frac{e^{- j k R_{m n}}}{R_{m n}} \\ R_{m n} = \sqrt{{(x - x^{'} - x_{m})}^{2} + {(y - y^{'} - y_{n})}^{2} + {(z - z^{'})}^{2}} \\ ϕ_{m n} = k (x_{m} \sin θ потому что φ + y_{n} \sin θ потому что φ) \\ x_{m} = m \cdot d_{x}, y_{n} = n \cdot d_{y} \end{array}$

Функция Грина

Периодическая функция Грина

$\begin{array}{l} g = \frac{e^{- j k R}}{R} \\ R = | \vec{r} - {\vec{r}}^{'} | \end{array}$

$\begin{array}{l} g_{периодический} = \sum_{m = - \infty}^{\infty} \sum_{n = - \infty}^{\infty} e^{j ϕ_{m n}} \frac{e^{- j k R_{m n}}}{R_{m n}} \\ R_{m n} = \sqrt{{(x - x^{'} - x_{m})}^{2} + {(y - y^{'} - y_{n})}^{2} + {(z - z^{'})}^{2}} \\ ϕ_{m n} = k (x_{m} \sin θ потому что φ + y_{n} \sin θ потому что φ) \\ x_{m} = m \cdot d_{x}, y_{n} = n \cdot d_{y} \end{array}$

_dx и _dy являются наземными размерностями плоскости, которые задают x и размерности y элементарной ячейки. θ и Φ являются углами сканирования.

Периодическая функция Грина имеет дополнительный экспоненциальный термин, добавленный к бесконечной сумме. Термин _Φmn составляет сканирование бесконечного массива. Периодическая функция Грина также составляет эффект взаимной связи.

Создайте массив Бога Используя Antenna Toolbox

Чтобы создать бесконечный массив, используйте объект infiniteArray повторить один элемент антенны (элементарная ячейка), бесконечно вдоль плоскости X-Y. Функция layout отображает типичную элементарную ячейку.

infarray = infiniteArray;
layout(infarray)

Выберите элементарную ячейку

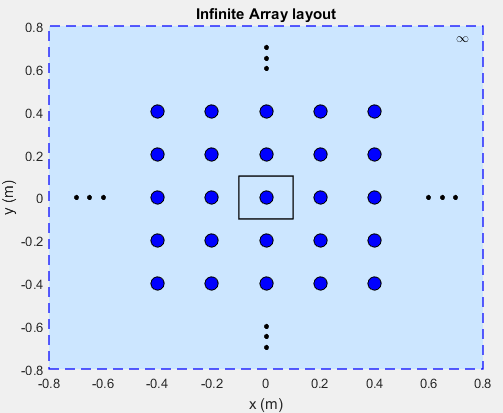
Можно использовать любую антенну от Antenna Toolbox™ как элементарная ячейка. Элементарная ячейка требует, чтобы наземная плоскость задала контуры. Можно использовать отражатель, чтобы поддержать антенны, которые не имеют наземной плоскости.

Свойства отражателя по умолчанию:

r = reflector

 reflector with properties:

              Exciter: [1x1 dipole]
    GroundPlaneLength: 0.2000
     GroundPlaneWidth: 0.2000
              Spacing: 0.0750
                 Tilt: 0
             TiltAxis: [1 0 0]

Элементарная ячейка по умолчанию в бесконечном массиве является отражателем, который имеет диполь как возбудитель. Свойство Spacing дает расстояние между отражателем и возбудителем. Бесконечные свойства массива по умолчанию:

infarray = infiniteArray

 infiniteArray with properties:

          Element: [1x1 reflector]
      ScanAzimuth: 0
    ScanElevation: 90

show (infarray)

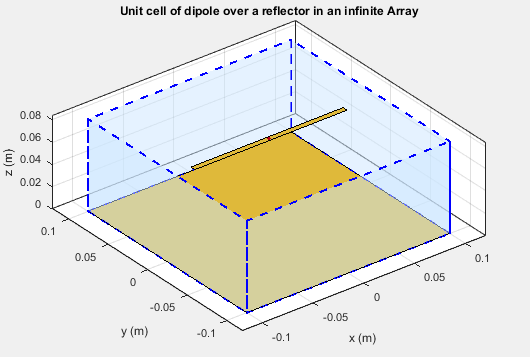
Точечное синее поле ограничивает элементарную ячейку. Оснуйте плоскую длину и основывайтесь, плоская ширина элементарной ячейки размерности элемента антенны бесконечного массива.

Антенна с наземной плоскостью, такой как микрополосковая антенна закрашенной фигуры, задана непосредственно как Element бесконечного массива.

infarray = infiniteArray('Element', patchMicrostrip)

infarray = 
  infiniteArray with properties:

          Element: [1x1 patchMicrostrip]
      ScanAzimuth: 0
    ScanElevation: 90

show(infarray)

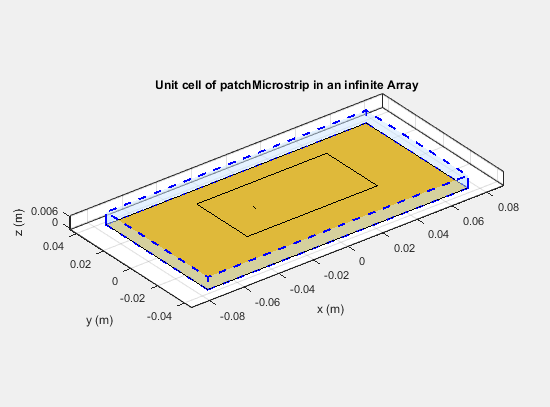
Antenna Toolbox бесконечный массив расположен в плоскости X-Y. Элементарные ячейки, состоящие из антенн с наземными плоскостями, также расположены в плоскости X-Y. Для антенн, используемых в качестве элементарных ячеек, таких как та в этом примере, вы игнорируете значение свойства Tilt.

Отсканируйте массивы Бога

Вы сканируете конечный массив путем определения соответствующего сдвига фазы для каждого элемента антенны. В Antenna Toolbox вы задаете угол сканирования (в азимуте и повышении) и частота для бесконечного анализа массивов. По умолчанию массив всегда сканирует в опорном направлении (азимут = 0 градусов и повышение = 90 градусов).

infarray = infiniteArray

 infiniteArray with properties:

          Element: [1x1 reflector]
      ScanAzimuth: 0
    ScanElevation: 90

Чтобы изменить углы сканирования, измените значения ScanAzimuth и ScanElevation.

Отсканируйте импеданс и отсканируйте шаблон элемента

Чтобы вычислить импеданс сканирования для бесконечного массива, используйте функцию impedance в качестве функции угла сканирования. Фиксация пары угла сканирования и развертка переменной частоты показывают зависимость от частоты в импедансе сканирования. Поскольку ScanAzimuth и ScanElevation являются скалярными значениями, вы должны for - цикл, чтобы вычислить полный импеданс сканирования массива. Для получения дополнительной информации о вычислении импеданса сканирования и шаблона элемента сканирования смотрите, Анализ Бога Массивов.

Отсканируйте шаблон элемента

Чтобы вычислить шаблон элемента сканирования с помощью импеданса сканирования, используйте эти выражения:

$g_{s} (θ) = \frac{4 R_{g} R_{ISO} g_{ISO} (θ)}{{| Z_{s} (θ) + Z_{g} |}^{2}}$

R _g — Сопротивление генератора
Z _g — Импеданс генератора
Z _s — Отсканируйте импеданс
_ISO g (θ) — Шаблон изолированного элемента
_ISO R — Сопротивление изолированного элемента

Шаблон элемента сканирования может также быть выражен с точки зрения отражательного коэффициента, Γ (θ):

$g_{s} (θ) = \frac{4 R_{ISO} g_{ISO} (θ)}{R_{s} (θ)} (1 - {| Γ (θ) |}^{2})$

Программное обеспечение Antenna Toolbox вычисляет шаблон элемента сканирования конечного массива путем управления только одним элементом. Вы отключаете все другие элементы с помощью подходящего импеданса. Получившийся шаблон элемента включает взаимную связь и допустим для всех углов сканирования.

Сравните шаблон элемента сканирования массивов Бога и конечных

Случай 1: Сравните конечный массив и бесконечный массив с элементарной ячейкой размерностей 0.5λ × 0.5λ

Чтобы вычислить шаблон элемента сканирования конечных массивов, во-первых, создают поддержанный отражателем диполь. Установите дипольные размерности на $Длина (L) = 0.495 λ$ и $Width (W) = λ / 160$ и наземные размерности плоскости к 0.5λ × 0.5λ. Поместите диполь на расстоянии h = λ/4 от отражателя. Наземные размерности плоскости устанавливают контуры элементарной ячейки. Создайте конечные массивы размеров 11x11, 15x15 и 17x17 с помощью этой элементарной ячейки.

Для конечных массивов вычислите шаблон элемента сканирования путем управления одним элементом в массиве. Отключите все другие конечные элементы массива с помощью поперечного сопротивления бесконечного массива. Для бесконечного массива с элементарной ячейкой размерностей 0.5λ × 0.5λ, поперечное сопротивление является 176 Ω. Вычислите шаблон элемента сканирования для Электронного, D-и H-плоскостей всех трех конечных массивов.

Чтобы вычислить шаблон элемента сканирования бесконечного массива, создайте бесконечный массив с помощью той же элементарной ячейки и класса infiniteArray. Вычислите импеданс сканирования для трех плоскостей сканирования: E, D, и H. Вычислите шаблон изолированного элемента (диполь, поддержанный отражателем). Наконец, используйте уравнения от предыдущего раздела, чтобы сгенерировать шаблон элемента сканирования для бесконечного массива.

Выполните весь анализ на уровне 10 ГГц. Чтобы сравнить шаблоны конечного и бесконечного массива, наложите их на том же графике.

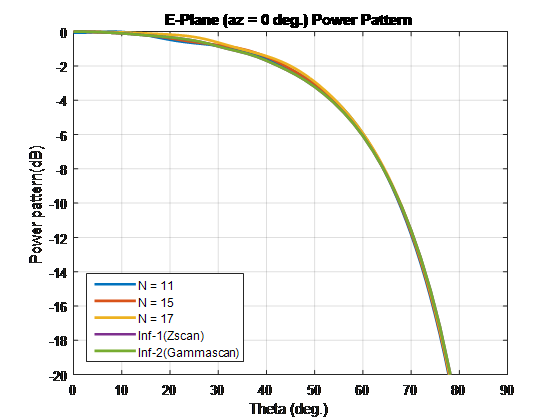
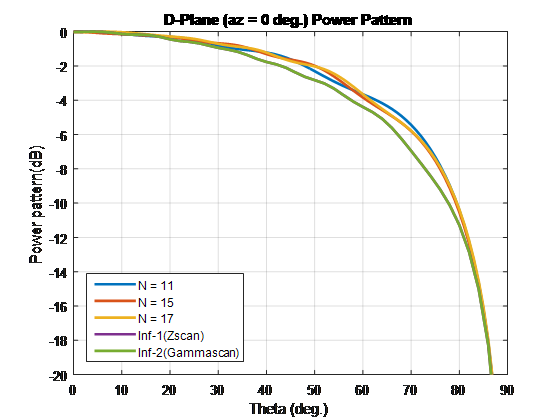
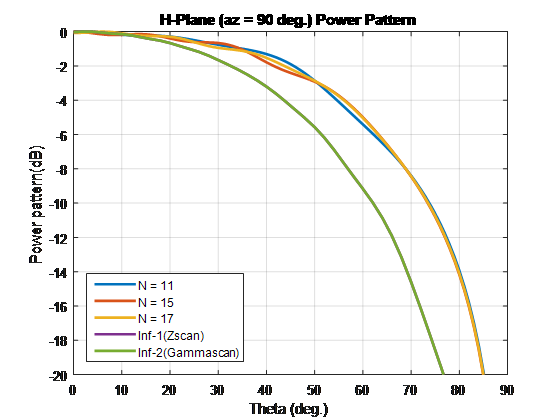
Случай 2: Сравните конечный массив и бесконечный массив с элементарной ячейкой размерностей 0.7λ × 0.7λ

Чтобы сравнить шаблон элемента сканирования этих типов массива и бесконечных массивов, повторите процесс в случае, если 1. Используя эти размерности элементарной ячейки создает скрипучие лепестки. Отключите конечные массивы с помощью 86-Ω сопротивлений. Для бесконечного массива с элементарной ячейкой размерностей 0.7λ × 0.7λ, поперечное сопротивление является 86 Ω.

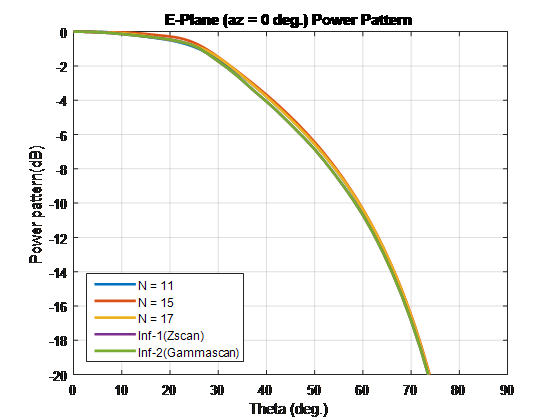
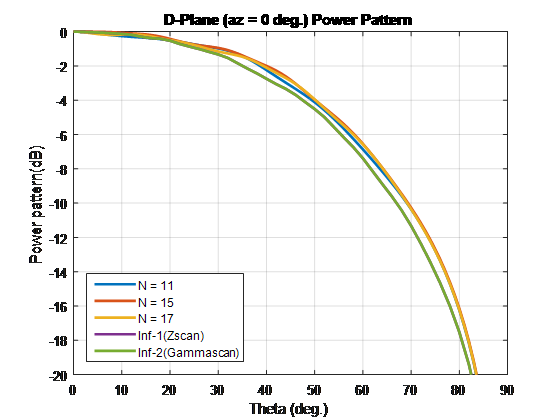
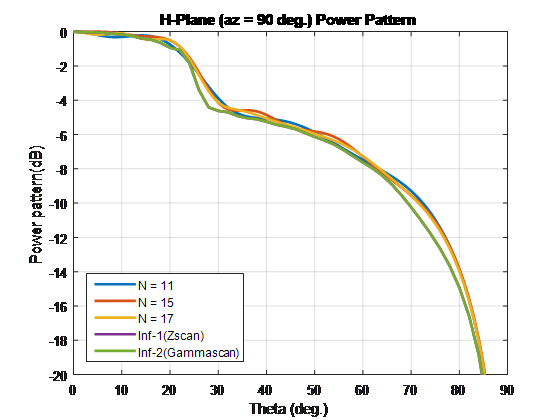
Для конечных массивов размера, больше, чем 10 x 10, шаблоны элемента сканирования в Электронном, D-и H-плоскостях совпадают с шаблонами бесконечного элемента сканирования массивов.

Влияние Бога двойное суммирование

Как показывают в уравнениях Зеленого, периодическая функция Грина имеет бесконечное двойное суммирование в (m, n). При выполнении бесконечного анализа массивов количество условий в двойном суммировании влияет на точность конечного решения. Более высокое количество условий приводит к лучшей точности, но время вычисления увеличений.

По умолчанию Antenna Toolbox использует термины 10 для каждого срока суммирования (m, n), чтобы выполнить бесконечный анализ массивов. Общая продолжительность срока суммирования 2*10+1 (-10 к +10). Чтобы изменить количество условий, используйте метод numSummationTerms.

Более высокое количество условий требуется если:

Вы наблюдаете отрицательные величины для сопротивления сканирования для определенных углов сканирования на определенных частотах.
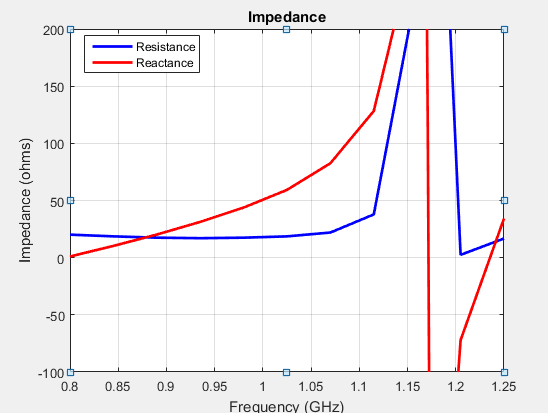
Необходимо заняться расследованиями для сходимости, когда импеданс сканирования показывает медленные изменения.

Ссылки

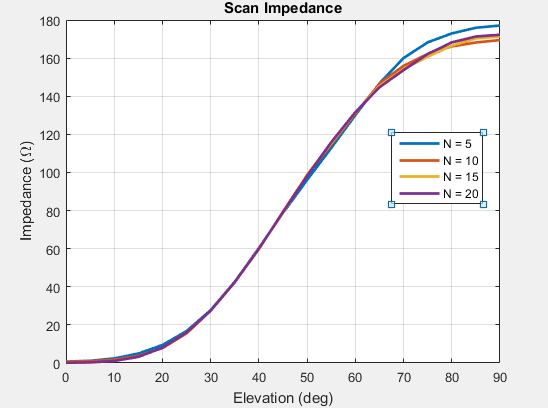
[1] Mailloux, R. J. Поэтапное руководство антенны массивов. Норвуд, MA: дом Artech. 2-й выпуск. 2005.

[2] Хансен, Р. К. Фэзед Аррей Антеннас. Хобокен, NJ: John Wiley & Sons Inc. 2-й Выпуск. 1998, стр 221–313.

[3] Аллен, J. "Усиление и изменение импеданса в отсканированных дипольных массивах". Транзакции IRE на Антеннах и Распространении. Издание 10, Номер 5, сентябрь 1962, стр 566–572.

[4] Wasylkiwskyj, W. и В. Кан. "Эффективность как мера размера антенны поэтапного массива". Транзакции IEEE на Антеннах и Распространении. Издание 21, Номер 6, ноябрь 1973, стр 879–884.

[5] Holter, H. и Х. Стеискэл. "На требовании размера для конечных поэтапных моделей массивов". Транзакции IEEE на Антеннах и Распространении. Издание 50, Номер 6, июнь 2002, стр 836–840.

Документация