Метод решателя моментов для металлических и диэлектрических структур

Метод метода вычисления Моментов для металлических и диэлектрических антенн.

Антенны с помощью диэлектрической подложки состоят из металлической детали и диэлектрической части. Первый шаг в вычислительном решении электромагнитных проблем должен дискретизировать Уравнения Максвелла. Процесс приводит к этой матрично-векторной системе:

$V = Z I$

V— Прикладной вектор напряжения. Этот сигнал может быть напряжением, или степень применилась к антенне или инцидентному сигналу, падающему на антенну.
Я — Текущий вектор, который представляет текущий на поверхности антенны.
Z Матрица взаимодействия или матрица импеданса, которая имеет отношение V ко мне. Для вычисления матрицы взаимодействия эффект металлических и диэлектрических частей в антенне взят отдельно.

Antenna Toolbox™ использует метод моментов (MoM), чтобы вычислить матрицу взаимодействия и решить системные уравнения.

Формулировка MoM

Формулировка MoM разделена в три части.

Дискретизация диэлектриков

Дискретизация включает формулировку от непрерывной области до дискретной области. Этот шаг называется, сцепляясь в литературе антенны. В формулировке MoM металлическая поверхность антенны поймана в сети в треугольники, и диэлектрический объем пойман в сети в четырехгранники.

Основные функции

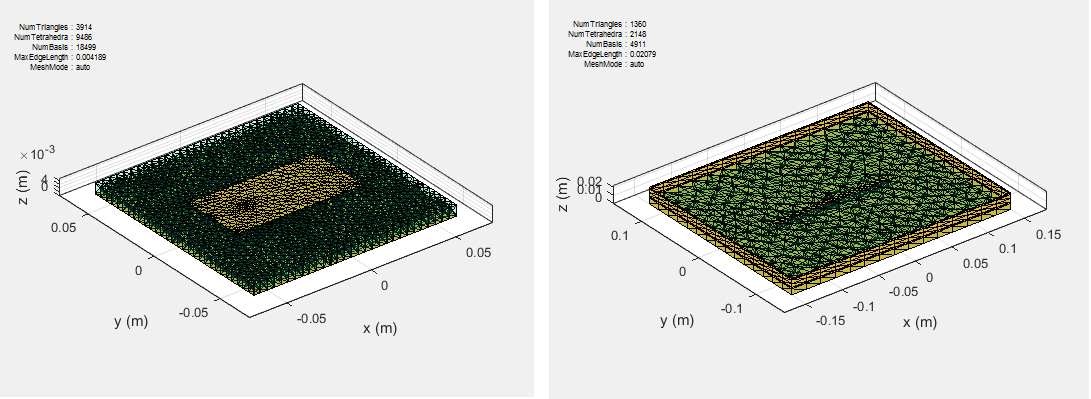
Основные функции используются, чтобы представлять неизвестные количества. В случае антенн с помощью диэлектриков неизвестные количества являются поверхностным током на металлической структуре и плотности потока из-за диэлектрического объема. Antenna Toolbox использует Рао-Вилтон-Глиссона (RWG) [2] основные функции. Поскольку основные функции для металлической структуры в антенне относятся, Метод Решателя Моментов для Металлических Структур.

Для диэлектрического объема антенны Antenna Toolbox использует нулевую основную функцию ребра порядка, чтобы смоделировать плотность потока.

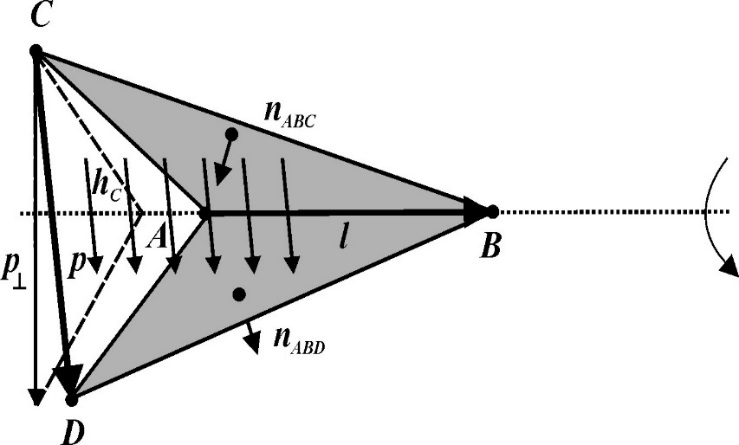
Данные показывают основанную на ребре основную функцию. Векторное изменение перпендикулярно основному AB ребра (или $\bar{l}$ ). Вектор CD ребра (или $\bar{p}$ ) задает основную функцию. В четырехграннике основная функция является постоянным полем, данным

$\vec{f} = c \vec{p}$

c коэффициент нормализации.
p вектор ребра, задающего основную функцию.

Матрица взаимодействия

Матрица взаимодействия является комплексной плотной симметрической матрицей. Для металлически-диэлектрической антенны существует два набора основных функций и четыре взаимодействия. Чтобы заполнить матрицу взаимодействия, вычислите функцию Грина свободного пространства между всеми основными функциями на поверхности антенны. Итоговые матричные уравнения взаимодействия:

_ZMM – металл к металлическому взаимодействию. Для чистой металлической структуры вы только вычисляете эту симметричную квадратную матрицу.
$Z_{m n}^{M M} = (\frac{j ω μ}{4 π}) \int_{S} \int_{S} {\vec{f}}^{M}_{m} (\vec{r}) . {\vec{f}}^{M}_{n} (\vec{r^{'}}) g d \vec{r^{'}} d \vec{r} - (\frac{j}{4 π ω ε}) \int_{S} \int_{S} (\nabla . {\vec{f}}^{M}_{m}) (\nabla . {\vec{f}}^{M}_{n}) g d \vec{r^{'}} d \vec{r}$
_ZDD – диэлектрик к диэлектрическому взаимодействию. Для чистых диэлектрических структур вы только вычисляете эту симметричную квадратную матрицу.
$\begin{array}{l} {\hat{Z}}_{m n}^{D D} = \sum_{p - 1}^{P} \sum_{p^{'} - 1}^{P^{'}} \frac{K_{p}}{{\hat{ε}}_{p}} \int_{V_{D}} {\vec{f}}_{m p} (\vec{r}) \cdot {\vec{f}}_{n p^{'}} (\vec{r}) d \vec{r} \\ - \frac{ω^{2} μ_{0}}{4 π} \sum_{p - 1}^{P} \sum_{p^{'} - 1}^{P^{'}} K_{p} K_{p^{'}} \int_{V_{D}} \int_{V_{D^{'}}} g (\vec{r}, \vec{r^{'}}) {\vec{f}}_{m p} (\vec{r}) \cdot {\vec{f}}_{n p^{'}} (\vec{r^{'}}) d \vec{r} d \vec{r^{'}} \\ - \frac{1}{4 π ε_{0}} \sum_{q - 1}^{Q} \sum_{q^{'} - 1}^{Q^{'}} {\hat{K}}_{q} {\hat{K}}_{q^{'}} \int_{Ω_{q}} \int_{Ω_{q^{'}}} g (\vec{r}, \vec{r^{'}}) f_{⊥ m q} (\vec{r}) f_{⊥ n q^{'}} (\vec{r^{'}}) d_{s} d_{s^{'}} m, n = 1, ...., N \end{array}$
_ZMD и _ZDM – Эти матрицы вычисляют взаимодействие между металлом и диэлектриком. Эта матрица не является симметричной квадратной матрицей.
$\begin{array}{l} Z_{m n}^{M D} = - \frac{ω^{2} μ_{0}}{4 π} \sum_{p - 1}^{2} \sum_{p^{'} - 1}^{P^{'}} K_{p} \int_{t} \int_{V_{D^{'}}} {\vec{f}}_{n}^{M} (\vec{r}) \cdot {\vec{f}}_{m p^{'}} (\vec{r^{'}}) g (\vec{r}, \vec{r^{'}}) d \vec{r^{'}} d_{s} \\ - \frac{1}{4 π ε_{0}} \sum_{p - 1}^{2} \sum_{q - 1}^{Q} {\hat{K}}_{q} \int_{t_{D}} \int_{Ω_{q^{'}}} (\nabla_{s} \cdot {\vec{f}}_{n}^{M} (\vec{r})) f_{⊥ m q} (\vec{r^{'}}) g (\vec{r}, \vec{r^{'}}) d_{Ω^{'}} d_{s} \\ m = 1, ...., N_{D}; n = 1, ..., N_{M} \end{array}$
$\begin{array}{l} Z_{m n}^{D M} = - \frac{j ω μ_{0}}{4 π} \sum_{p - 1}^{2} \sum_{p^{'} - 1}^{P^{'}} K_{p^{'}} \int_{V_{D}} \int_{S_{D^{'}}} {\vec{f}}_{n p} (\vec{r}) \cdot {\vec{f}}_{m}^{M} (\vec{r^{'}}) g (\vec{r}, \vec{r^{'}}) d_{s^{'}} d \vec{r} \\ + \frac{1}{4 π ε_{0} ω} \sum_{p - 1}^{2} \sum_{q - 1}^{Q} {\hat{K}}_{q} \int_{Ω_{q}} \int_{S_{D^{'}}} f_{⊥ n q} (\vec{r}) \cdot (\nabla_{s} \cdot {\vec{f}}_{m}^{M} (\vec{r^{'}})) g (\vec{r}, \vec{r^{'}}) d_{s^{'}} d_{Ω} \\ m = 1, ...., N_{D}; n = 1, ..., N_{M} \end{array}$

где

$g (\vec{r}, \vec{r^{'}}) = \frac{\exp (- j k R)}{R}, R = | \vec{r} - \vec{r^{'}} |$ функция Грина свободного пространства.
$K = \frac{{\hat{ε}}^{\pm} - ε_{0}}{{\hat{ε}}^{\pm}}$ комплексная диэлектрическая постоянная в каждом четырехграннике.
${\hat{K}}_{q} = K_{+} - K_{-}$ дифференциальный контраст на каждой поверхности четырехгранника.

Для составной металлической структуры необходимо вычислить все четыре матрицы.

Соседняя область

Данные показывают типичную матрицу взаимодействия для металлической структуры _ZMM с 256 основными функциями.

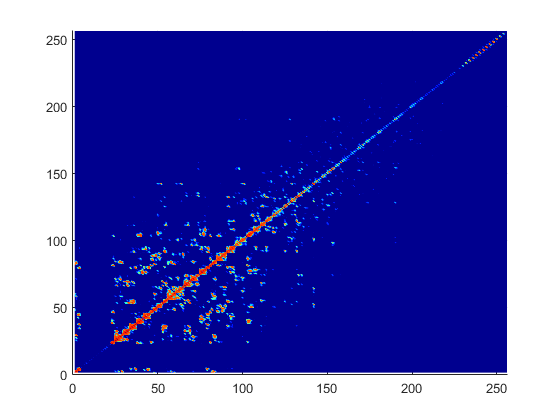
Из матричного графика взаимодействия вы замечаете, что матрица является по диагонали доминирующей. Диэлектрическая матрица взаимодействия является также по диагонали доминирующей. Когда вы перемещаетесь еще дальше от диагонали, значения уменьшений условий. Это поведение - то же самое как поведение функции Грина. Функция Грина уменьшается как расстояние между увеличениями r' и r. Поэтому важно вычислить область на диагональ и близко к диагонали точно.

Эта область на и вокруг диагонали называется соседней областью. Для металлически-диэлектрической антенны область окружения основана на среднем размере четырехгранника.

Для граничения с деталями области для металлических антенн относятся, Метод Решателя Моментов для Металлических Структур.

Экстракция особенности

По диагонали r и r' идентичны, и заданная функция Грина становится сингулярной. Чтобы удалить особенность, экстракция выполняется на этих условиях. Уравнения для экстракции особенности матрицы _ZMM:

$\begin{array}{l} \int_{t_{p}} \int_{t_{q}} ({\vec{ρ}}_{i} . {\vec{ρ}}^{'}_{j}) g (\vec{r}, \vec{r^{'}}) d s' d s = \int_{t_{p}} \int_{t_{q}} \frac{({\vec{ρ}}_{i} . {\vec{ρ}}^{'}_{j})}{| \vec{r} - \vec{r^{'}} |} d s' d s + \int_{t_{p}} \int_{t_{q}} \frac{(\exp (- j k | \vec{r} - \vec{r^{'}} |) - 1) ({\vec{ρ}}_{i} . {\vec{ρ}}^{'}_{j})}{| \vec{r} - \vec{r^{'}} |} d s' d s \\ \int_{t_{p}} \int_{t_{q}} g (\vec{r}, \vec{r^{'}}) d s' d s = \int_{t_{p}} \int_{t_{q}} \frac{1}{| \vec{r} - \vec{r^{'}} |} d s' d s + \int_{t_{p}} \int_{t_{q}} \frac{(\exp (- j k | \vec{r} - \vec{r^{'}} |) - 1)}{| \vec{r} - \vec{r^{'}} |} d s' d s \end{array}$

Эти два интеграла на правой стороне уравнений, названных потенциальными или статическими интегралами, найдены с помощью аналитических результатов [3].

Уравнения для экстракции особенности матрицы _ZDD:

$\begin{array}{l} \int_{V_{D}} \int_{V_{D^{'}}} g (\vec{r}, \vec{r^{'}}) d \vec{r} d \vec{r^{'}} = \int_{V_{D}} \int_{V_{q}} \frac{1}{| \vec{r} - \vec{r^{'}} |} d \vec{r} d \vec{r^{'}} + \int_{V_{D}} \int_{V_{q}} \frac{(\exp (- j k | \vec{r} - \vec{r^{'}} |) - 1)}{| \vec{r} - \vec{r^{'}} |} d \vec{r} d \vec{r^{'}} \\ \int_{Ω_{q}} \int_{Ω_{q^{'}}} g (\vec{r}, \vec{r^{'}}) d Ω d Ω' = \int_{Ω_{D}} \int_{Ω_{q}} \frac{1}{| \vec{r} - \vec{r^{'}} |} d Ω d Ω' + \int_{S_{D}} \int_{S_{q}} \frac{(\exp (- j k | \vec{r} - \vec{r^{'}} |) - 1)}{| \vec{r} - \vec{r^{'}} |} d Ω d Ω \end{array}$

Конечные массивы

Формулировка MoM для конечных массивов эквивалентна для одного элемента антенны. Основным различием является количество возбуждений (подача). Для конечных массивов вектор напряжения является теперь матрицей напряжения. Количество столбцов равно числу элементов в массиве.

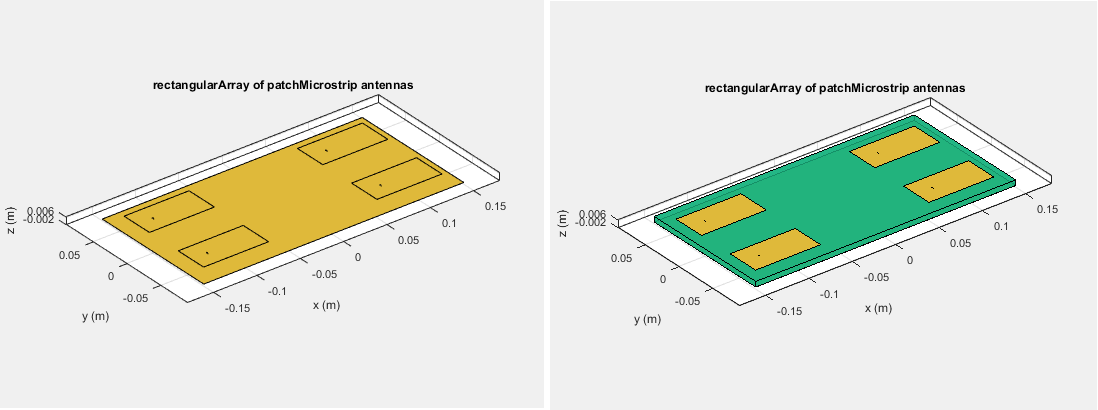
Например, матрица вектора напряжения для массива 2x2 прямоугольной антенны закрашенной фигуры (с и без диэлектрической подложки) имеет четыре столбца, когда каждая антенна может быть взволнована отдельно.

Массив Бога

Чтобы смоделировать бесконечный массив, вы изменяете MoM, чтобы составлять бесконечное поведение. Для этого вы заменяете функции Грина свободного пространства на периодические функции Грина. Периодическая функция Грина является бесконечным двойным суммированием.

Функция Грина	Периодическая функция Грина
$\begin{array}{l} g = \frac{e^{- j k R}}{R} \\ R = \| \vec{r} - {\vec{r}}^{'} \| \end{array}$	$\begin{array}{l} g_{периодический} = \sum_{m = - \infty}^{\infty} \sum_{n = - \infty}^{\infty} e^{j ϕ_{m n}} \frac{e^{- j k R_{m n}}}{R_{m n}} \\ R_{m n} = \sqrt{{(x - x^{'} - x_{m})}^{2} + {(y - y^{'} - y_{n})}^{2} + {(z - z^{'})}^{2}} \\ ϕ_{m n} = k (x_{m} \sin θ потому что φ + y_{n} \sin θ потому что φ) \\ x_{m} = m \cdot d_{x}, y_{n} = n \cdot d_{y} \end{array}$

Функция Грина

Периодическая функция Грина

$\begin{array}{l} g = \frac{e^{- j k R}}{R} \\ R = | \vec{r} - {\vec{r}}^{'} | \end{array}$

$\begin{array}{l} g_{периодический} = \sum_{m = - \infty}^{\infty} \sum_{n = - \infty}^{\infty} e^{j ϕ_{m n}} \frac{e^{- j k R_{m n}}}{R_{m n}} \\ R_{m n} = \sqrt{{(x - x^{'} - x_{m})}^{2} + {(y - y^{'} - y_{n})}^{2} + {(z - z^{'})}^{2}} \\ ϕ_{m n} = k (x_{m} \sin θ потому что φ + y_{n} \sin θ потому что φ) \\ x_{m} = m \cdot d_{x}, y_{n} = n \cdot d_{y} \end{array}$

d _x и d _y являются наземными размерностями плоскости, которые задают x и размерности y элементарной ячейки. θ и Φ являются углами сканирования.

Сравнивая эти две функции Грина, вы наблюдаете дополнительный экспоненциальный термин, который добавляется к бесконечной сумме. _Φmn составляет сканирование бесконечного массива. Периодическая функция Грина также составляет эффект взаимной связи.

Для получения дополнительной информации смотрите, Массивы Бога.

Ссылки

[1] Harringhton, R. F. Полевое вычисление методами момента. Нью-Йорк: Макмиллан, 1968.

[2] Рао, S. M. Д. Р. Вилтон и А. В. Глиссон. “Электромагнитное рассеивание поверхностями произвольной формы”. IEEE. Сделка. Антенны и Распространение, издание AP-30, № 3, май 1982, стр 409–418.

[3] Вильтон, D. R. С. М. Рао, А. В. Глиссон, Д. Х. Шоберт, О. М. Аль-Бундак. и К. М. Батлер. “Потенциальные Интегралы для универсального и линейного исходного распределения на многоугольных и многогранных областях”. IEEE. Сделка. Антенны и Распространение. Издание AP-30, № 3, май 1984, стр 276–281.

[4] Balanis, C.A. Теория антенны. Анализ и проектирование. 3-й Эд. Нью-Йорк: John Wiley & Sons, 2005.

Документация