Разработайте контроллер сервомотора LQR в Simulink

Следующие данные показывают, что блок-схема Simulink^® показывает проблему отслеживания в проекте автопилота самолета. Чтобы открыть эту схему, введите lqrpilot в подсказке MATLAB^®.

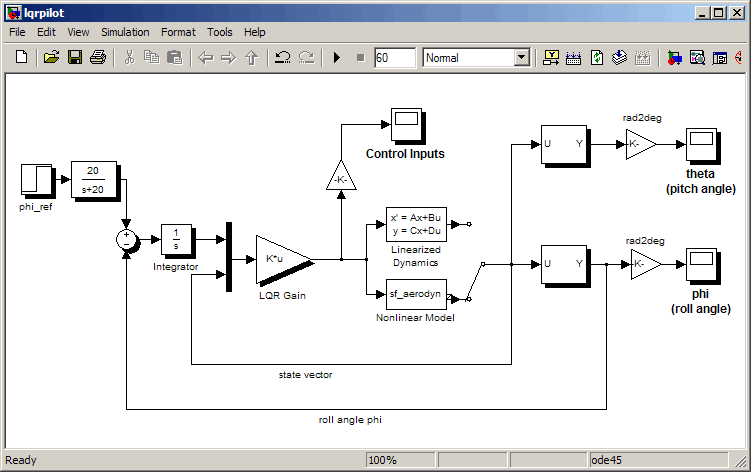
Ключевые возможности этой схемы, чтобы отметить следующие:

Блок Linearized Dynamics содержит линеаризовавший корпус.
sf_aerodyn является Блок s-function, который содержит нелинейные уравнения для $(θ, ϕ) = (0, 15^{\circ})$ .
Сигнал ошибки между $ϕ$ и $ϕ_{r e f}$ передается через интегратор. Это помогает в управлении ошибкой обнулить.

Уравнения пространства состояний для корпуса

Начало со стандартного уравнения пространства состояний

$\dot{x} = A x + B u$

где

$x = {[u, v, w, p, q, r, θ, ϕ]}^{T}$

Переменные u, v и w являются этими тремя скоростями относительно каркаса кузова, показанного можно следующим образом.

Кадр координаты тела для самолета

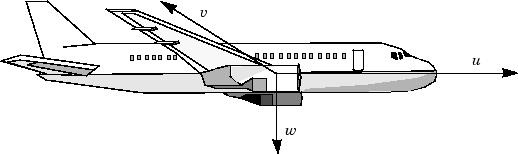
Переменные $ϕ$ и $θ$ список и подача, и p, q, и r является списком, подачей и уровнями отклонения от курса, соответственно.

Движущие силы корпуса нелинейны. Следующее уравнение показывает нелинейные компоненты, добавленные к уравнению пространства состояний.

Нелинейный компонент уравнения пространства состояний

$\dot{x} = A x + B u + [\begin{matrix} - g \sin θ \\ g потому что θ \sin ϕ \\ g потому что θ потому что ϕ \\ 000 \\ q потому что ϕ - r \sin ϕ \\ (q \sin ϕ + r потому что ϕ) \cdot загар θ \end{matrix}]$

Чтобы видеть численные значения для A и B, ввести

load lqrpilot
A, B

в посдказке MATLAB.

Обрезка

В целях проекта LQG нелинейные движущие силы обрезаются в $ϕ = 15^{\circ}$ и p, q, r и θ обнуляются. Начиная с u v и w не вводят в нелинейный термин в предыдущей фигуре, это составляет линеаризацию вокруг $(θ, ϕ) = (0, 15^{\circ})$ со всеми остающимися обнуленными состояниями. Получившаяся матрица состояния линеаризовавшей модели называется A15.

Проблемное определение

Цель выполнить устойчивый скоординированный поворот, как показано в этой фигуре.

Самолет, делающий поворот на 60 °

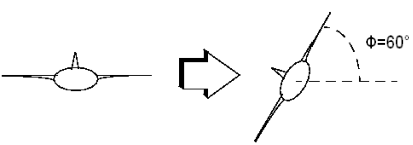
Чтобы достигнуть этой цели, необходимо разработать контроллер, который управляет устойчивым поворотом путем прохождения через списка на 60 °. Кроме того, примите, что θ, угол подачи, требуется, чтобы оставаться максимально близко к нулю.

Результаты

Вычислить матрицу усиления LQG, K, тип

lqrdes

в посдказке MATLAB. Затем запустите модель lqrpilot с нелинейной модели, sf_aerodyn, выбранного.

Эти данные показывают ответ $ϕ$ к команде шага на 60 °.

Отслеживание команды шага списка

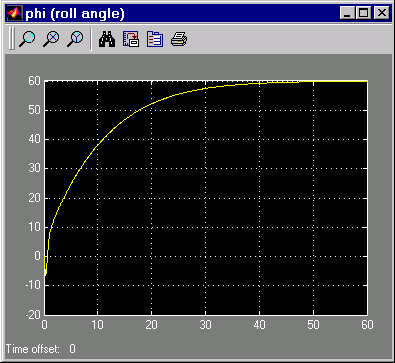
Как вы видите, системные дорожки, 60 °, которыми управляют, сыплют приблизительно 60 секунд.

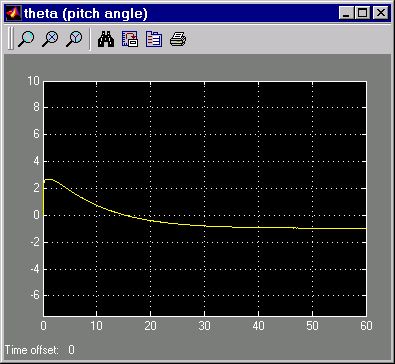
Другая цель состояла в том, чтобы сохранить θ, угол подачи, относительно маленький. Эти данные показывают, как хорошо контроллер LQG сделал.

Минимизируя смещение в углу подачи, тете

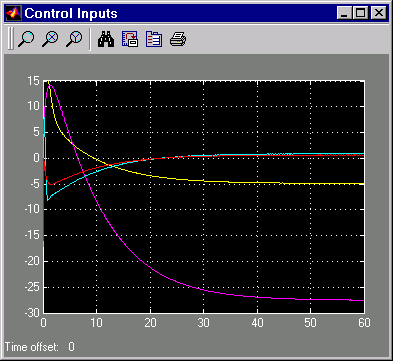
Наконец, эти данные показывают входные параметры управления.

Управляйте входными параметрами для LQG отслеживание проблемы

Попытайтесь настроить Q и матрицы R в lqrdes.m и осмотреть входные параметры управления и системные состояния, убедившись повторно выполнять lqrdes, чтобы обновить усиление LQG матричный K. Методом проб и ошибок можно улучшить время отклика этого проекта. Кроме того, сравните линейные и нелинейные проекты, чтобы видеть эффекты нелинейности на производительности системы.

Документация