Пользовательский нелинейный анализ данных ENSO

Этот пример соответствует данным ENSO с помощью нескольких пользовательских нелинейных уравнений. Данные ENSO состоят из ежемесячных усредненных различий в атмосферном давлении между островом Пасхи и Дарвином, Австралия. Это различие управляет торговыми ветрами в южном полушарии.

Данные ENSO являются явно периодическими, который предполагает, что они могут быть описаны рядом Фурье:

$y (x) = a_{0} + \sum_{i = 1}^{\infty} a_{i} потому что (2 π \frac{x}{c_{i}}) + b_{i} \sin (2 π \frac{x}{c_{i}})$

где _ai и _bi являются амплитудами, и _ci является периодами (циклы) данных. Вопрос ответить вот состоит в том, сколько циклов существует?

Как первая попытка, примите один цикл и соответствуйте данным, использующим один термин косинуса и один термин синуса.

$y_{1} (x) = a_{0} + a_{1} потому что (2 π \frac{x}{c_{1}}) + b_{1} \sin (2 π \frac{x}{c_{1}})$

Если подгонка не описывает данные хорошо, добавьте дополнительный косинус и условия синуса с уникальными коэффициентами периода, пока хорошая подгонка не получена.

Уравнение нелинейно, потому что неизвестный коэффициент c ₁ включен как часть аргументов тригонометрической функции.

Загрузите данные и подходящую библиотеку и пользовательские модели Фурье

Загрузите данные и откройте приложение Curve Fitting:
```
load enso
cftool
```
Тулбокс включает ряд Фурье как нелинейное уравнение библиотеки. Однако уравнение библиотеки не удовлетворяет потребности этого примера, потому что его условия заданы как зафиксированные множители основной частоты w. Обратитесь к Ряду Фурье для получения дополнительной информации. Создайте встроенную библиотеку подгонка Фурье, чтобы соответствовать вашим пользовательским уравнениям:
1. Выберите month for X data и pressure for Y data.
2. Выберите Fourier для типа модели.
3. Введите Fourier для Fit name.
4. Измените количество условий к 8.
  Наблюдайте подгонку модели библиотеки. На следующих шагах вы создадите пользовательские уравнения, чтобы выдержать сравнение.
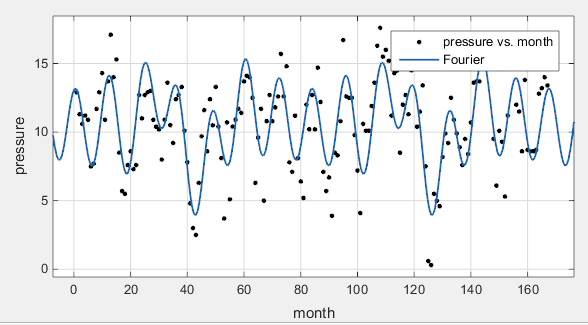
Копируйте свою подгонку. Щелкните правой кнопкой по своей подгонке по Table of Fits и выберите Duplicate ‘Fourier’.
Назовите новый подходящий Enso1Period.
Измените подходящий тип от Fourier до Custom Equation.
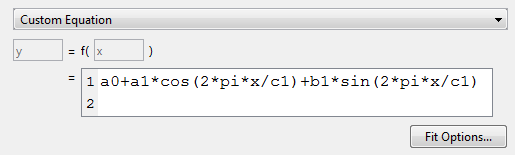
Замените текст в качестве примера в окне редактирования уравнения с
```
a0+a1*cos(2*pi*x/c1)+b1*sin(2*pi*x/c1)
```
Тулбокс применяет подгонку к данным enso.

Графические и числовые результаты, показанные здесь, показывают, что подгонка не описывает данные хорошо. В частности, подходящее значение для c1 является необоснованно маленьким. Ваши начальные результаты подгонки могут отличаться от этих результатов, потому что отправные точки случайным образом выбраны.

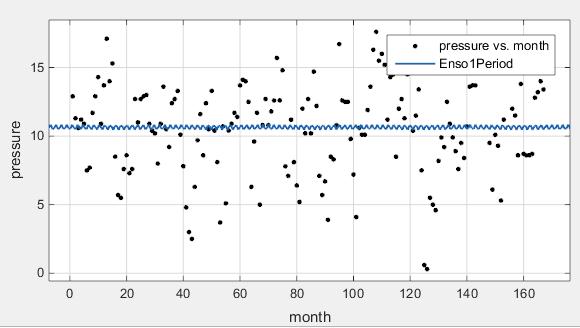
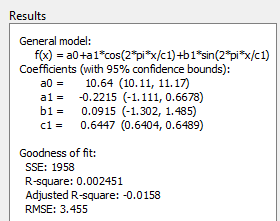
По умолчанию коэффициенты неограниченны и имеют случайные начальные значения от 0 до 1. Данные включают периодический компонент с периодом приблизительно 12 месяцев. Однако с неограниченным c1 и со случайной отправной точкой, этой подгонке не удалось найти тот цикл.

Используйте подходящие опции, чтобы ограничить коэффициент

Чтобы помочь подходящей процедуре, ограничьте c1 к значению от 10 до 14. Нажмите кнопку Fit Options, чтобы просмотреть и отредактировать ограничения для неизвестных коэффициентов.
В Подходящем Окне параметров заметьте, что по умолчанию коэффициенты неограниченны (границы -Inf и Inf).
Измените Lower и границы Upper для c1, чтобы ограничить цикл с 10 до 14 месяцев, как показано затем.
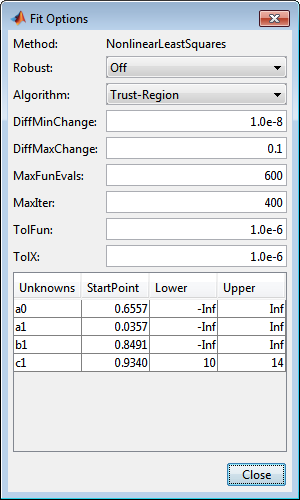
Нажмите Close. Ремонты приложения Curve Fitting.
Наблюдайте новую подгонку и график невязок. При необходимости выберите View> Residuals Plot или используйте кнопку на панели инструментов.
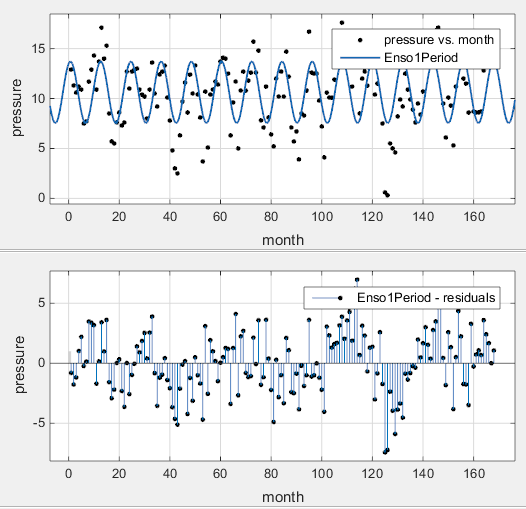
Подгонка, кажется, разумна для некоторых точек данных, но ясно не описывает целый набор данных очень хорошо. Как предсказано, числовые результаты в панели Results (c1=11.94) показывают на цикл приблизительно 12 месяцев. Однако невязки показывают систематическое периодическое распределение, указывая, что, по крайней мере, еще один цикл существует. Существуют дополнительные циклы, которые необходимо включать в подходящее уравнение.

Создайте вторую подгонку на заказ с дополнительными условиями и ограничениями

Чтобы совершенствовать вашу подгонку, необходимо добавить дополнительный синус и термин косинуса к y ₁ (x) можно следующим образом:

$y_{2} (x) = y_{1} (x) + a_{2} потому что (2 π \frac{x}{c_{2}}) + b_{2} \sin (2 π \frac{x}{c_{2}})$

и ограничьте верхние и нижние границы c ₂ быть примерно дважды границами, используемыми для c ₁.

Копируйте свою подгонку путем щелчка правой кнопкой по нему по Table of Fits и выбора Duplicate ‘Enso1Period’.
Назовите новый подходящий Enso2Period.
Добавьте эти условия в конец предыдущего уравнения:
```
+a2*cos(2*pi*x/c2)+b2*sin(2*pi*x/c2)
```
Нажмите Fit Options. Когда вы редактируете пользовательское уравнение, инструмент помнит ваши подходящие опции. Наблюдайте Lower, и границы Upper для c1 все еще ограничивают цикл с 10 до 14 месяцев. Добавьте более подходящие опции:
1. Измените Lower и Upper для c2, чтобы быть примерно дважды границами, используемыми для c1 (20 <c2 <30).
2. Измените StartPoint для a0 к 5.
Когда вы изменяете каждые настройки, ремонты приложения Curve Fitting. Подгонку и невязки показывают затем.

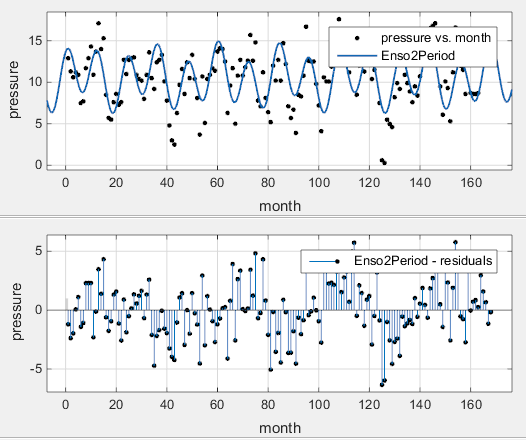
Подгонка кажется разумной для большинства точек данных. Однако невязки указывают, что необходимо включать другой цикл в подходящее уравнение.

Создайте третью подгонку на заказ с дополнительными условиями и ограничениями

Как третья попытка, добавьте дополнительный синус и термин косинуса к y ₂ (x)

$y_{3} (x) = y_{2} (x) + a_{3} потому что (2 π \frac{x}{c_{3}}) + b_{3} \sin (2 π \frac{x}{c_{3}})$

и ограничьте нижнюю границу c ₃ быть примерно тройной значение c ₁.

Копируйте свою подгонку путем щелчка правой кнопкой по нему по Table of Fits и выбора Duplicate ‘Enso2Period’.
Назовите новый подходящий Enso3Period.
Добавьте эти условия в конец предыдущего уравнения:
```
+a3*cos(2*pi*x/c3)+b3*sin(2*pi*x/c3)
```
Нажмите Fit Options Observe, ваши предыдущие подходящие опции все еще присутствуют.
1. Измените Lower, направляющийся в c3, чтобы быть 36, который является примерно тройным значение c1.
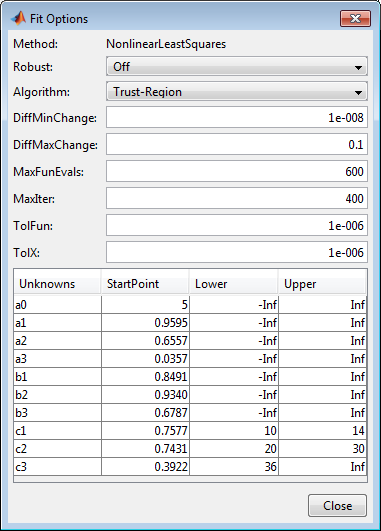
2. Закройте диалоговое окно. Ремонты приложения Curve Fitting. Подгонка и невязки появляются затем.

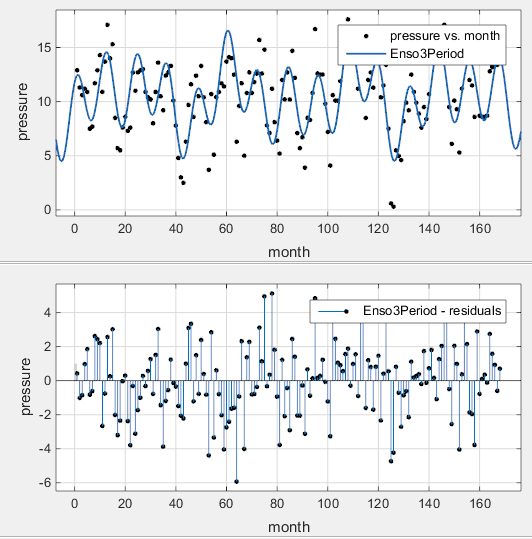
Подгонка является улучшением по сравнению с предыдущими двумя подгонками и, кажется, составляет большинство циклов в наборе данных ENSO. Невязки кажутся случайными для большинства данных, несмотря на то, что шаблон является все еще видимым указанием, что могут присутствовать дополнительные циклы, или можно улучшить подходящие амплитуды.

В заключение анализ Фурье данных показывает три значительных цикла. Ежегодный цикл является самым сильным, но циклы с периодами приблизительно 44 и 22 месяцев также присутствуют. Эти циклы соответствуют Эль-Ниньо и южному Колебанию (ENSO).

Документация