Ряд Фурье

О серийных моделях Фурье

Ряд Фурье является суммой синусоидальных и косинусных функций, которая описывает периодический сигнал. Это представлено или в тригонометрической форме или в экспоненциальной форме. Тулбокс обеспечивает эту тригонометрическую серийную форму Фурье

$y = a_{0} + \sum_{i = 1}^{n} a_{i} потому что (i w x) + b_{i} \sin (i w x)$

где модели a₀, константа (прерывание), термин в данных и сопоставлен с i = 0 терминов косинуса, w, является основной частотой сигнала, n, являются количеством условий (гармоники) в ряду и 1 ≤ n ≤ 8.

Для получения дополнительной информации о ряде Фурье, обратитесь к Фурье - анализу и фильтрации посредством Фурье-преобразования (MATLAB).

Соответствуйте моделям Фурье в интерактивном режиме

Откройте приложение Curve Fitting путем ввода cftool. Также нажмите Curve Fitting на вкладке Apps.
В приложении Curve Fitting выберите данные о кривой (X data и Y data, или только Y data против индекса).
Приложение Curve Fitting создает подгонку кривой по умолчанию, Polynomial.
Измените тип модели от Polynomial до Fourier.

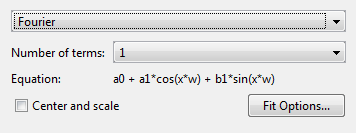
Можно задать следующие опции:

Выберите количество условий: 1 к 8.
Посмотрите в панели Results, чтобы видеть образцовые условия, значения коэффициентов и статистику качества подгонки.
(Необязательно) Нажмите Fit Options, чтобы задать содействующие начальные значения и ограничительные границы, или изменить настройки алгоритма.
Тулбокс вычисляет оптимизированные стартовые точки для серийных моделей Фурье, на основе текущего набора данных. Можно заменить стартовые точки и задать собственные значения в Подходящем Окне параметров.
Для получения дополнительной информации о настройках см. Опции Подгонки Определения и Оптимизированные Отправные точки.

Для примера, сравнивающего библиотеку подгонка Фурье с пользовательскими уравнениями, смотрите Пользовательский Нелинейный Анализ данных ENSO.

Соответствуйте Моделям Фурье Используя подходящую Функцию

Скрипт Open Live Script

Этот пример показывает, как использовать функцию fit, чтобы соответствовать модели Фурье к данным.

Модель библиотеки Фурье является входным параметром к функциям fittype и fit. Задайте тип модели fourier, сопровождаемый количеством условий, например, 'fourier1' к 'fourier8'.

Этот пример соответствует данным о Южном Эль-Ниньо колебании (ENSO). Данные ENSO состоят из ежемесячных усредненных различий в атмосферном давлении между островом Пасхи и Дарвином, Австралия. Это различие управляет торговыми ветрами в южном полушарии.

Данные ENSO являются явно периодическими, который предполагает, что они могут быть описаны рядом Фурье. Используйте серийные модели Фурье, чтобы искать периодичность.

Соответствуйте 2D термину модель Фурье

Загрузите некоторые данные и соответствуйте 2D термину модель Фурье.

load enso;
f = fit(month,pressure,'fourier2')

f = 
     General model Fourier2:
     f(x) =  a0 + a1*cos(x*w) + b1*sin(x*w) + 
               a2*cos(2*x*w) + b2*sin(2*x*w)
     Coefficients (with 95% confidence bounds):
       a0 =       10.63  (10.23, 11.03)
       a1 =       2.923  (2.27, 3.576)
       b1 =       1.059  (0.01593, 2.101)
       a2 =     -0.5052  (-1.086, 0.07532)
       b2 =      0.2187  (-0.4202, 0.8576)
       w =      0.5258  (0.5222, 0.5294)

plot(f,month,pressure)

Доверительные границы на a2 и b2 пересекают нуль. Для линейных членов вы не можете быть уверены, что эти коэффициенты отличаются от нуля, таким образом, они не помогают с подгонкой. Это означает, что эти две модели термина, вероятно, не лучше, чем одна модель термина.

Измерьте период

Термин w является мерой периода. 2*pi/w преобразовывает в период в месяцах, потому что периодом sin() и cos() является 2*pi.

w = f.w

w = 0.5258

2*pi/w

ans = 11.9497

w очень близко к 12 месяцам, указывая на ежегодный период. Заметьте, что это выглядит правильным на графике с peaks на расстоянии приблизительно в 12 месяцев.

Соответствуйте модели Фурье с восемью терминами

f2 = fit(month,pressure,'fourier8')

f2 = 
     General model Fourier8:
     f2(x) = 
               a0 + a1*cos(x*w) + b1*sin(x*w) + 
               a2*cos(2*x*w) + b2*sin(2*x*w) + a3*cos(3*x*w) + b3*sin(3*x*w) + 
               a4*cos(4*x*w) + b4*sin(4*x*w) + a5*cos(5*x*w) + b5*sin(5*x*w) + 
               a6*cos(6*x*w) + b6*sin(6*x*w) + a7*cos(7*x*w) + b7*sin(7*x*w) + 
               a8*cos(8*x*w) + b8*sin(8*x*w)
     Coefficients (with 95% confidence bounds):
       a0 =       10.63  (10.28, 10.97)
       a1 =      0.5668  (0.07981, 1.054)
       b1 =      0.1969  (-0.2929, 0.6867)
       a2 =      -1.203  (-1.69, -0.7161)
       b2 =     -0.8087  (-1.311, -0.3065)
       a3 =      0.9321  (0.4277, 1.436)
       b3 =      0.7602  (0.2587, 1.262)
       a4 =     -0.6653  (-1.152, -0.1788)
       b4 =     -0.2038  (-0.703, 0.2954)
       a5 =    -0.02919  (-0.5158, 0.4575)
       b5 =     -0.3701  (-0.8594, 0.1192)
       a6 =    -0.04856  (-0.5482, 0.4511)
       b6 =     -0.1368  (-0.6317, 0.3581)
       a7 =       2.811  (2.174, 3.449)
       b7 =       1.334  (0.3686, 2.3)
       a8 =     0.07979  (-0.4329, 0.5925)
       b8 =     -0.1076  (-0.6037, 0.3885)
       w =     0.07527  (0.07476, 0.07578)

plot(f2,month,pressure)

Измерьте период

w = f2.w

w = 0.0753

(2*pi)/w

ans = 83.4736

С моделью f2 период w составляет приблизительно 7 лет.

Исследуйте условия

Ищите коэффициенты с самым большим значением, чтобы найти самые важные условия.

a7 и b7 являются самыми большими. Посмотрите на уравнение члена в модели a7: a7*cos(7*x*w). 7*w == 7/7 = цикл 1 года. a7 и b7 указывают, что ежегодный цикл является самым сильным.
Точно так же a1 и условия b1 дают 7/1, указывая на семилетний цикл.
a2 и условия b2 являются циклом 3,5 лет (7/2). Это более сильно, чем 7-летний цикл, потому что a2 и коэффициенты b2 имеют большее значение, чем a1 и b1.
a3 и b3 являются довольно сильными выражениями, указывающими на 7/3 или цикл 2,3 лет.
Меньшие условия менее важны для подгонки, таковы как a6, b6, a5 и b5.

Как правило, нагревание Эль-Ниньо происходит в неправильных интервалах двух - семи лет и длится девять месяцев к двум годам. Средняя длина периода составляет пять лет. Образцовые результаты отражают некоторые из этих периодов.

Установите стартовые точки

Тулбокс вычисляет оптимизированные стартовые точки для подгонок Фурье, на основе текущего набора данных. Серийные модели Фурье особенно чувствительны к отправным точкам, и оптимизированные значения могут быть точными только для нескольких условий в связанных уравнениях. Можно заменить стартовые точки и задать собственные значения.

После исследования условий и графиков, похоже, что 4-летний цикл может присутствовать. Попытайтесь подтвердить это установкой w. Получите значение для w, где 8 лет = 96 месяцев.

w = (2*pi)/96

w = 0.0654

Найдите порядок записей для коэффициентов в модели ('f2') при помощи функции coeffnames.

coeffnames(f2)

ans = 18x1 cell array
    {'a0'}
    {'a1'}
    {'b1'}
    {'a2'}
    {'b2'}
    {'a3'}
    {'b3'}
    {'a4'}
    {'b4'}
    {'a5'}
    {'b5'}
    {'a6'}
    {'b6'}
    {'a7'}
    {'b7'}
    {'a8'}
    {'b8'}
    {'w' }

Получите текущие содействующие значения.

coeffs = coeffvalues(f2)

coeffs = 1×18

   10.6261    0.5668    0.1969   -1.2031   -0.8087    0.9321    0.7602   -0.6653   -0.2038   -0.0292   -0.3701   -0.0486   -0.1368    2.8112    1.3344    0.0798   -0.1076    0.0753

Установите последний коэффициент, w, к 0,065.

coeffs(:,18) = w

coeffs = 1×18

   10.6261    0.5668    0.1969   -1.2031   -0.8087    0.9321    0.7602   -0.6653   -0.2038   -0.0292   -0.3701   -0.0486   -0.1368    2.8112    1.3344    0.0798   -0.1076    0.0654

Установите стартовые точки для коэффициентов с помощью нового значения для w.

f3 = fit(month,pressure,'fourier8', 'StartPoint', coeffs);

Постройте обе подгонки, чтобы видеть, что новое значение для w в f3 не производит лучшую подгонку, чем f2.

plot(f3,month,pressure)
hold on
plot(f2, 'b')
hold off
legend( 'Data', 'f3', 'f2')

Найдите, что Фурье соответствует опциям

Найдите доступные подходящие опции с помощью fitoptions(modelname), где modelname является типом модели fourier, сопровождаемый количеством условий, например, 'fourier1' к 'fourier8'.

fitoptions('fourier8')

ans =

        Normalize: 'off'
          Exclude: []
          Weights: []
           Method: 'NonlinearLeastSquares'
           Robust: 'Off'
       StartPoint: [1x0 double]
            Lower: [1x0 double]
            Upper: [1x0 double]
        Algorithm: 'Trust-Region'
    DiffMinChange: 1.0000e-08
    DiffMaxChange: 0.1000
          Display: 'Notify'
      MaxFunEvals: 600
          MaxIter: 400
           TolFun: 1.0000e-06
             TolX: 1.0000e-06

Если вы хотите изменить подходящие опции, такие как содействующие начальные значения, и ограничительные границы, подходящие для ваших данных, или изменить настройки алгоритма, видят опции для NonlinearLeastSquares на странице с описанием fitoptions.

Смотрите также

fit | fitoptions | fittype

Документация