Сравните помещается в приложение Curve Fitting

Интерактивный рабочий процесс Curve Fitting

Следующие темы соответствуют некоторым данным о переписи с помощью полиномиальных уравнений до шестой степени и экспоненциального уравнения одно термина. Шаги демонстрируют как к:

  • Загрузите данные и исследуйте различные подгонки с помощью различных моделей библиотеки.

  • Ищите лучшую подгонку:

    • Сравнение графических результатов подгонки

    • Сравнение числовых результатов подгонки включая подходящие коэффициенты и статистику качества подгонки

  • Экспортируйте свои лучшие результаты подгонки в рабочую область MATLAB®, чтобы анализировать модель в командной строке.

  • Сохраните сеанс и сгенерируйте код MATLAB для всех подгонок и графики.

Загрузка данных и создание подгонок

Необходимо загрузить переменные данных в рабочее пространство MATLAB, прежде чем можно будет соответствовать данным с помощью приложения Curve Fitting. В данном примере данные хранятся в файле MATLAB census.mat.

  1. Загрузите данные:

    load census

    Рабочая область содержит две новых переменные:

    • cdate является вектор-столбцом, содержащим годы 1790 - 1990 с 10-летним шагом.

    • pop является вектор-столбцом с американскими фигурами генеральной совокупности, которые соответствуют годам в cdate.

  2. Откройте приложение Curve Fitting:

    cftool

  3. Выберите имена переменных cdate и pop из списков Y data и X data.

    Приложение Curve Fitting создает и строит подгонку по умолчанию к X входам (или данные о предикторе) и Y вывод (или данные об ответе). Подгонка по умолчанию является линейным типом аппроксимации полиномом. Заметьте, что подходящие настройки отображают Polynomial Degree 1.

  4. Измените подгонку к второму полиному степени путем выбора 2 из списка Degree.

    Приложение Curve Fitting строит новую подгонку. Приложение Curve Fitting вычисляет новую подгонку, когда вы изменяете подходящие настройки, потому что Auto fit выбран по умолчанию. Если переоборудование является трудоемким, например, для больших наборов данных, можно выключить Auto fit путем снятия флажка.

    Результаты отображений приложения Curve Fitting подбора кривой данным о переписи с квадратичным полиномом в панели Результатов, где можно просмотреть модель библиотеки, адаптированные коэффициенты и статистику качества подгонки.

  5. Измените Fit name на poly2.

  6. Отобразите невязки путем выбора View> Residuals Plot.

    Невязки указывают, что лучшая подходящая сила возможна. Поэтому продолжите исследовать различные подгонки к набору данных переписи.

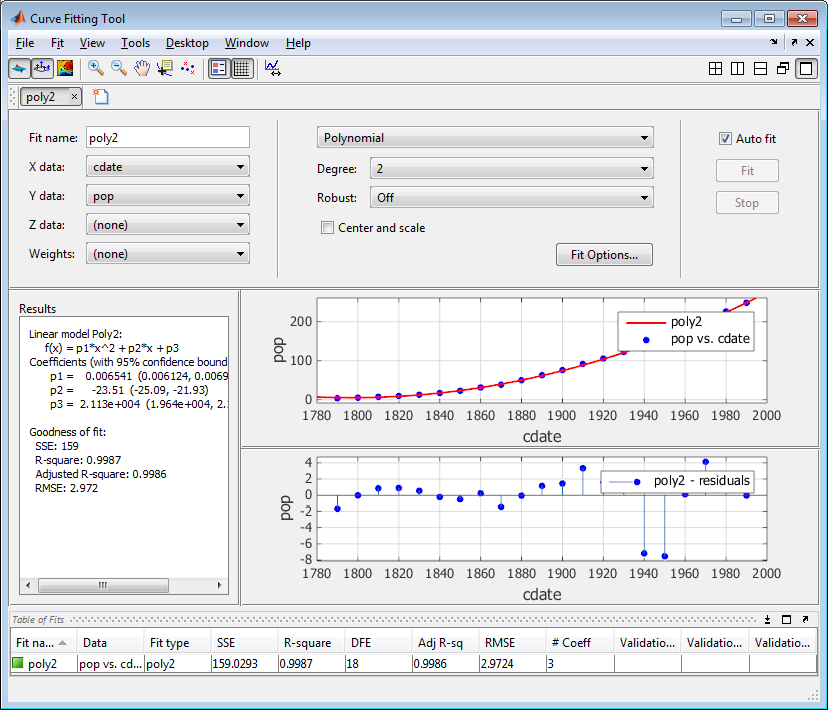
  7. Добавьте новые подгонки, чтобы попробовать другие уравнения библиотеки.

    1. Щелкните правой кнопкой по подгонке по Table of Fits и выберите Duplicate “poly2” (или используйте меню Fit).

      Совет

      Для припадков данного типа (например, полиномы), Duplicate “fitname” использования вместо новой подгонки, потому что копирование подгонки требует меньшего количества шагов. Дублированная подгонка содержит те же выборы данных и подходящие настройки.

    2. Измените полиномиальный Degree на 3 и переименуйте подходящий poly3.

    3. Когда вы соответствуете более высоким полиномам степени, панель Результатов выводит это предупреждение:

      Equation is badly conditioned. Remove repeated data points
or try centering and scaling.

      Нормируйте данные путем выбора флажка шкалы и Center.

    4. Повторите шаги a и b, чтобы добавить аппроксимации полиномом до шестой степени, и затем добавить экспоненциальное приближение.

    5. Для каждой новой подгонки посмотрите на информацию о панели Results и график невязок в приложении Curve Fitting.

      Невязки от хорошей подгонки должны выглядеть случайными без очевидного шаблона. Шаблон, такой как тенденция для последовательных невязок, чтобы иметь тот же знак, может быть индикацией, что существует лучшая модель.

О масштабировании

Предупреждение о масштабировании возникает, потому что подходящая процедура использует значения cdate в качестве основания для матрицы с очень большими значениями. Распространение значений cdate приводит к масштабирующейся проблеме. Чтобы решить эту проблему, можно нормировать данные cdate. Нормализация масштабирует данные о предикторе, чтобы улучшить точность последующих числовых вычислений. Способ нормировать cdate состоит в том, чтобы сосредоточить его в нулевом среднем значении и масштабировать его к модульному стандартному отклонению. Эквивалентный код:

(cdate - mean(cdate))./std(cdate)

Примечание

Поскольку изменения данных о предикторе после нормализации, значения подходящих коэффициентов также изменяются когда по сравнению с исходными данными. Однако функциональная форма данных и получившейся статистики качества подгонки не изменяется. Кроме того, данные отображены в графиках приложения Curve Fitting с помощью исходной шкалы.

Определение лучшей подгонки

Чтобы определить лучшую подгонку, необходимо исследовать и графические и числовые результаты подгонки.

Исследуйте графические результаты подгонки

  1. Определите лучшую подгонку путем исследования графиков подгонок и невязок. Чтобы просмотреть графики для каждой подгонки в свою очередь, дважды кликните подгонку в Таблице Подгонок. Графические результаты подгонки указывают что:

    • Подгонки и невязки для полиномиальных уравнений все подобны, мешая выбирать лучшее.

    • Подгонка и невязки для одно термина экспоненциальное уравнение указывают, что это - плохая подгонка в целом. Поэтому это - плохой выбор, и можно удалить экспоненциальное приближение от кандидатов на лучшую подгонку.

  2. Исследуйте поведение подгонок до года 2050. Цель подбора кривой данным о переписи состоит в том, чтобы экстраполировать лучшую подгонку, чтобы предсказать будущие значения генеральной совокупности.

    1. Дважды кликните аппроксимацию полиномом шестой степени в Таблице Подгонок, чтобы просмотреть графики для этой подгонки.

    2. Измените пределы осей графиков путем выбора Tools> Axes Limits.

    3. Измените Maximum X (cdate) к 2050, и увеличьте Maximum Main Y (pop) до 400 и нажмите Enter.

    4. Исследуйте подходящий график. Поведение аппроксимации полиномом шестой степени вне области значений данных делает его плохим выбором для экстраполяции, и можно отклонить эту подгонку.

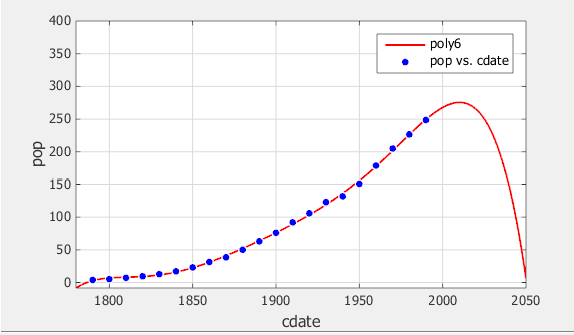
Оцените числовые результаты подгонки

Когда вы больше не можете устранять подгонки путем исследования их графически, необходимо исследовать числовые результаты подгонки. Отображения приложения Curve Fitting два типа числовых результатов подгонки:

  • Статистика качества подгонки

  • Доверительные границы на подходящих коэффициентах

Статистические данные качества подгонки помогают вам определить, как хорошо кривая соответствует данным. Доверительные границы на коэффициентах определяют свою точность.

Исследуйте числовые результаты подгонки:

  1. Для каждой подгонки просмотрите статистику качества подгонки в панели Results.

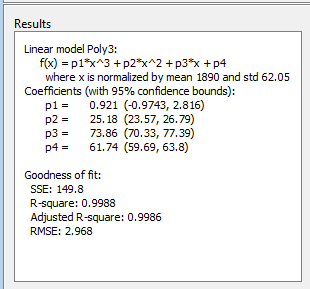
  2. Сравните все подгонки одновременно в Table of Fits. Кликните по заголовкам столбцов к виду результатами статистики.

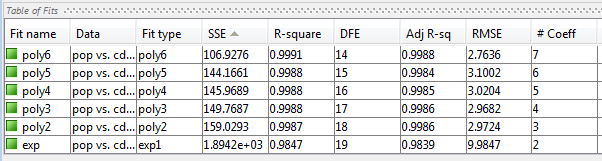
  3. Исследуйте сумму квадратов из-за ошибки (SSE) и настроенный R - квадратная статистика, чтобы помочь определить лучшую подгонку. Статистическая величина SSE является ошибкой наименьших квадратов подгонки со значением ближе, чтобы обнулить указание на лучшую подгонку. Настроенный R - квадратная статистическая величина является обычно лучшим индикатором подходящего качества, когда вы добавляете дополнительные коэффициенты в свою модель.

    Самый большой SSE для exp1 указывает, что это - плохая подгонка, который вы уже определенный путем исследования подгонки и невязок. Самое низкое значение SSE сопоставлено с poly6. Однако поведение этой подгонки вне области значений данных делает его плохим выбором для экстраполяции, таким образом, вы уже отклонили эту подгонку путем исследования графиков с новыми пределами по осям.

    Следующее лучшее значение SSE сопоставлено с аппроксимацией полиномом пятой степени, poly5, предположив, что это может быть лучшая подгонка. Однако SSE и настроенный R - квадратные значения для остающихся аппроксимаций полиномом являются всеми очень друг близко к другу. Какой необходимо выбрать?

  4. Решите лучший подходящий вопрос путем исследования доверительных границ на остающееся, помещается в панель Результатов. Дважды кликните подгонку в Table of Fits, чтобы открыться (или особое внимание, если уже открываются), подходящая фигура, и просмотрите панель Результатов. fit figure отображает подходящие настройки, панель результатов и графики для одной подгонки.

    Отобразите полином пятой степени и фигуры подгонки poly2 рядом. Исследование результатов рядом может помочь вам оценить подгонки.

    1. Чтобы показать двум подходящим фигурам одновременно, используйте средства управления размещением в правом верхнем из приложения Curve Fitting или выберите Window> Left/Right Tile или Top/Bottom Tile.

    2. Чтобы изменить отображенные подгонки, щелкните, чтобы выбрать подходящую фигуру и затем дважды кликнуть подгонку, чтобы отобразиться в Table of Fits.

    3. Сравните коэффициенты и границы (p1, p2, и так далее) в панели Результатов для обеих подгонок, poly5 и poly2. Тулбокс вычисляет 95% доверительных границ на коэффициенты. Доверительные границы на коэффициентах определяют свою точность. Проверяйте уравнения в панель Результатов (f(x)=p1*x+p2*x...), чтобы видеть образцовые условия для каждого коэффициента. Обратите внимание на то, что p2 относится к термину p2*x в Poly2 и термину p2*x^4 в Poly5. Не сравнивайте нормированные коэффициенты непосредственно с ненормированными коэффициентами.

      Совет

      Используйте меню View, чтобы скрыть Fit Settings или Table of Fits, если вы хотите, чтобы больше пробела просмотрело и сравнило графики и результаты, как показано затем. Можно также скрыть панель Results, чтобы показать только графики.

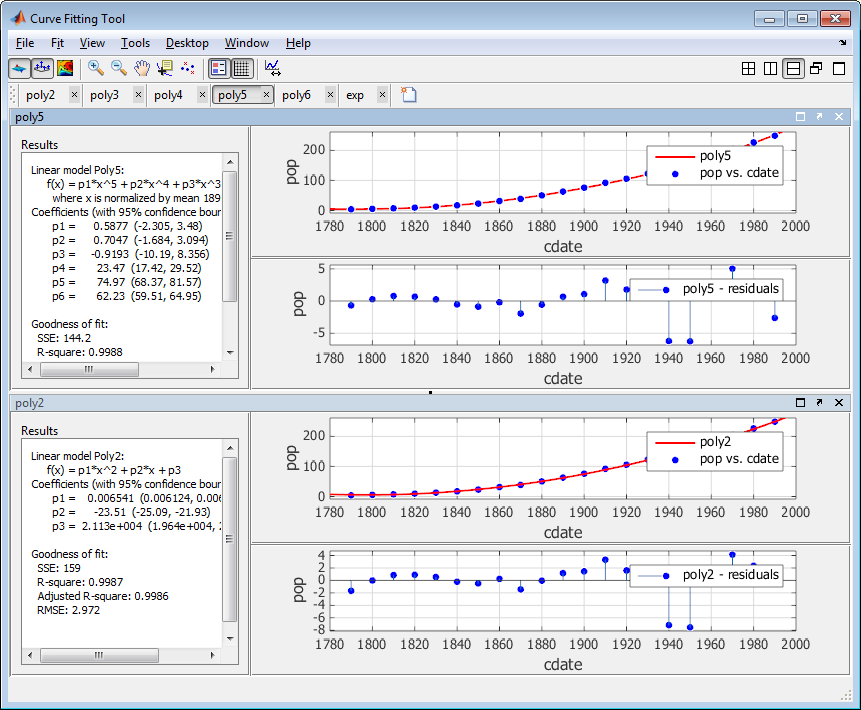
      Границы пересекают нуль на p1, p2 и коэффициентах p3 для полинома пятой степени. Это означает, что вы не можете быть уверены, что эти коэффициенты отличаются от нуля. Если условия модели высшего порядка могут иметь коэффициенты нуля, они не помогают с подгонкой, которая предполагает, что эта модель сверхсоответствует данным о переписи.

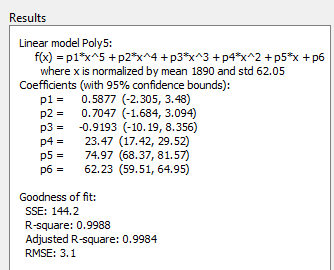
      Однако маленькие доверительные границы не пересекают нуль на p1, p2, и p3 для квадратичной подгонки, poly2 указывает, что подходящие коэффициенты известны справедливо точно.

      Поэтому после исследования и графические и числовые результаты подгонки, необходимо выбрать poly2 как лучшую подгонку, чтобы экстраполировать данные о переписи.

Примечание

Подходящие коэффициенты, сопоставленные с постоянными, линейными, и квадратичными условиями, почти идентичны для каждого нормированного полиномиального уравнения. Однако когда полиномиальная степень увеличивается, содействующие границы, сопоставленные с более высоким перекрестным нулем условий степени, который предлагает сверхсоответствовать.

Анализ ваше лучшее помещается в рабочую область

Можно использовать Save to Workspace, чтобы экспортировать выбранную подгонку и связанные результаты подгонки к рабочему пространству MATLAB. Подгонка сохранена как объект MATLAB, и связанные результаты подгонки сохранены как структуры.

  1. Щелкните правой кнопкой по poly2, помещаются в Table of Fits и выбирают Save “poly2” to Workspace (или используйте меню Fit).

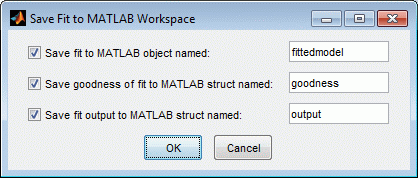
  2. Нажмите OK, чтобы сохранить с именами по умолчанию.

    fittedmodel сохранен как объект Curve Fitting Toolbox™ cfit.

    >> whos fittedmodel
  Name             Size            Bytes  Class

  fittedmodel      1x1               822  cfit

Исследуйте объект fittedmodel cfit отобразить модель, подходящие коэффициенты и доверительные границы для подходящих коэффициентов:

fittedmodel

fittedmodel =
     Linear model Poly2:
       fittedmodel(x) = p1*x^2 + p2*x + p3
     Coefficients (with 95% confidence bounds):
       p1 =    0.006541  (0.006124, 0.006958)
       p2 =      -23.51  (-25.09, -21.93)
       p3 =  2.113e+004  (1.964e+004, 2.262e+004)

Исследуйте структуру goodness, чтобы отобразить результаты качества подгонки:

goodness

goodness = 
           sse: 159.0293
       rsquare: 0.9987
           dfe: 18
    adjrsquare: 0.9986
          rmse: 2.9724

Исследуйте структуру output, чтобы отобразить дополнительную информацию, сопоставленную с подгонкой, такой как невязки:

output

output = 
       numobs: 21
     numparam: 3
    residuals: [21x1 double]
     Jacobian: [21x3 double]
     exitflag: 1
    algorithm: 'QR factorization and solve'
  iterations: 1

Можно оценить (интерполируйте или экстраполируйте), дифференцируйтесь или интегрируйте подгонку в заданной области значений данных с различными функциями постобработки.

Например, чтобы оценить fittedmodel в векторе значений, чтобы экстраполировать к году 2050, введите:

y = fittedmodel(2000:10:2050)
y =

  274.6221
  301.8240
  330.3341
  360.1524
  391.2790
  423.7137
Постройте подгонку к данным о переписи и экстраполируемым подходящим значениям:
plot(fittedmodel, cdate, pop)
hold on
plot(fittedmodel, 2000:10:2050, y)
hold off
Для большего количества примеров и инструкций для анализа подгонки интерактивной и командной строки и списка всех функций постобработки, считают целесообразным, Постобрабатывая.

Для примера, воспроизводящего этот интерактивный анализ данных переписи с помощью командной строки, смотрите Полиномиальный Curve Fitting.

Сохранение вашей работы

Тулбокс предоставляет несколько возможностей для сохранения вашей работы. Можно сохранить одну или несколько подгонок и связанные результаты подгонки как переменные к рабочему пространству MATLAB. Можно затем использовать эту сохраненную информацию в целях документации, или расширять исследование данных и анализ. В дополнение к сохранению вашей работы к переменным рабочего пространства MATLAB вы можете:

  • Сохраните текущий сеанс аппроксимирования кривыми путем выбора File> Save Session. Файл сеанса содержит все подгонки и переменные на вашем сеансе и помнит ваше размещение. Смотрите Сохраняют и Сеансы Перезагрузки.

  • Сгенерируйте код MATLAB, чтобы воссоздать все подгонки и графики в вашем сеансе путем выбора File> Generate Code. Приложение Curve Fitting генерирует код от вашего сеанса и отображает файл в редакторе MATLAB.

    Можно воссоздать подгонки и графики путем вызова файла в командной строке с исходными данными как входные параметры. Можно также вызвать файл с новыми данными и автоматизировать процесс подбора кривой нескольким наборам данных. Для получения дополнительной информации см. Генерирующийся Код из Приложения Curve Fitting.

Похожие темы

Документация Curve Fitting Toolbox
Поддержка
Для просмотра документации необходимо авторизоваться на сайте