Документация

Функции с векторным знаком

Тулбокс поддерживает сплайны с векторным знаком. Например, если вы хотите сплайновую кривую через данные плоские точки, затем следующий код задает некоторые данные и затем создает и строит такую сплайновую кривую, с помощью параметризации длины хорды и интерполяции кубическим сплайном с граничным условием не-узла.

x=[19 43 62 88 114 120 130 129 113 76 135 182 232 298 ...
 348 386 420 456 471 485 463 444 414 348 275 192 106 ...
 30 48 83 107 110 109 92 66 45 23 22 30 40 55 55 52 34 20 16];
y=[306 272 240 215 218 237 275 310 368 424 425 427 428 ...
 397 353 302 259 200 148 105 77 47 28 17 10 12 23 41 43 ...
 77 96 133 155 164 157 148 142 162 181 187 192 202 217 245 266 303];

xy = [x;y]; df = diff(xy,1,2); 
t = cumsum([0, sqrt([1 1]*(df.*df))]); 
cv = csapi(t,xy);
fnplt(cv), hold on, plot(x,y,'o'), hold off

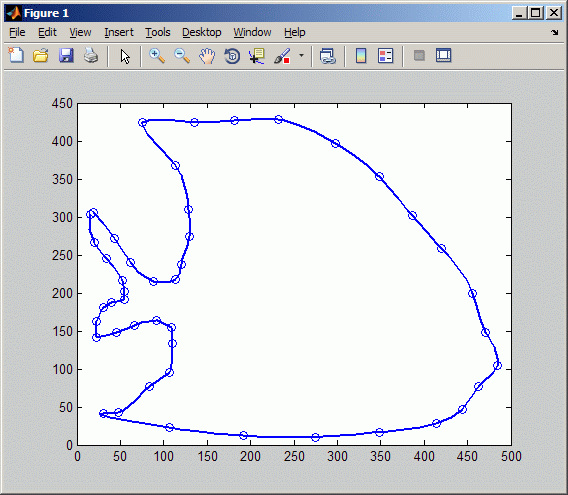
Если бы вы затем хотели знать область, заключенную этой кривой, вы хотели бы оценить интеграл с точкой на кривой, соответствующей значению параметров. Для сплайновой кривой в cv, только созданном, это может быть сделано точно в одном (несколько сложный) команда:

area = diff(fnval(fnint( ...
       fncmb(fncmb(cv,[0 1]),'*',fnder(fncmb(cv,[1 0]))) ...
                        ),fnbrk(cv,'interval')));

Чтобы объяснить, y=fncmb(cv,[0 1]) выбирает второй компонент кривой в cv, Dx=fnder(fncmb(cv,[1 0])) обеспечивает производную первого компонента, и yDx=fncmb(y,'*',Dx) создает их pointwise продукт. Затем IyDx=fnint(yDx) создает неопределенный интеграл yDx и, наконец, diff(fnval(IyDx,fnbrk(cv,'interval'))) оценивает тот неопределенный интеграл при конечных точках основного интервала и затем берет различие второго от первого значения, таким образом получая определенный интеграл yDx на его основном интервале. В зависимости от того, является ли вложенная область направо или налево когда точка кривой перемещается с увеличивающимся параметром, получившийся номер или положителен или отрицателен.

Далее, все значения Y (если таковые имеются), для которого точка (X,Y) находится на сплайновой кривой в cv, только созданном, могут быть получены следующим (несколько сложный) команда:

X=250; %Define a value of X
Y = fnval(fncmb(cv,[0 1]), ...
         mean(fnzeros(fncmb(fncmb(cv,[1 0]),'-',X))))

Объяснить: x = fncmb(cv,[1 0]) выбирает первый компонент кривой в cv; xmX = fncmb(x,'-',X) переводит тот компонент X; t = mean(fnzeros(xmX)) обеспечивает все значения параметров, для которого нуля xmX is , т.е. для который первый компонент кривой равняется X; y = fncmb(cv,[0,1]) выбирает второй компонент кривой в cv; и, наконец, Y = fnval(y,t) оценивает тот второй компонент на тех сайтах параметра, на которых первый компонент кривой в cv равняется X.

Как другой пример использования функций с векторным знаком, предположите, что вы решили уравнения движения частицы в некотором заданном силовом поле в плоскости, получении, в дискретные времена, положение, а также скорость, сохраненную в с 4 векторами, как вы были бы, если стандартным способом вы решили эквивалентную систему первого порядка численно. Затем следующий оператор, который использует кубическую интерполяцию Эрмита, произведет график частицы path:fnplt(spapi(augknt(t,4,2),t,reshape(z,2,2*n))).