Адаптивные фильтры нейронной сети

ADALINE (адаптивный линейный нейрон) сети, обсужденные в этой теме, подобны perceptron, но их передаточная функция линейна, а не трудно ограничивает. Это позволяет их выходным параметрам брать любое значение, тогда как perceptron вывод ограничивается или 0 или 1. И ADALINE и perceptron могут решить только линейно отделимые проблемы. Однако здесь LMS (наименьшее количество средних квадратичных) изучение правила, которое намного более мощно, чем perceptron изучение правила, используется. LMS или Видроу-Хофф, изучая правило минимизирует среднеквадратичную погрешность и таким образом перемещает контуры решения, насколько это может от учебных шаблонов.

В этом разделе вы разрабатываете адаптивную линейную систему, которая отвечает на изменения в ее среде, когда он действует. Линейные сети, которые настроены на каждом временном шаге на основе нового входа и предназначаются для векторов, могут найти веса и смещения, которые минимизируют квадратичную невязку суммы сети для недавнего входа и предназначаются для векторов. Сети этого вида часто используются в ошибочной отмене, обработке сигналов и системах управления.

Новаторская работа в этом поле была сделана Widrow и Hoff, который дал имени ADALINE адаптивным линейным элементам. Основной ссылкой на этом предмете является Widrow, B., и С.Д. Стернс, Адаптивная Обработка сигналов, Нью-Йорк, Prentice Hall, 1985.

Адаптивное обучение самоорганизующихся и конкурентоспособных сетей также рассматривается в этом разделе.

Адаптивные функции

Этот раздел вводит функциональный adapt, который изменяет веса и смещения сети инкрементно во время обучения.

Линейная модель нейрона

Линейный нейрон с входными параметрами R показывают ниже.

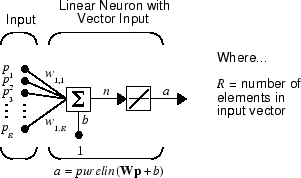
Эта сеть имеет ту же базовую структуру как perceptron. Единственная разница - то, что линейный нейрон использует линейную передаточную функцию, названную purelin.

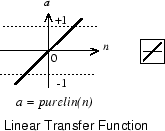
Линейная передаточная функция вычисляет, вывод нейрона путем простого возвращения значения передал ей.

α = purelin (n) = purelin (Wp + b) = Wp + b

Этот нейрон может быть обучен изучить аффинную функцию своих входных параметров или найти линейную аппроксимацию к нелинейной функции. Линейная сеть не может, конечно, быть сделана выполнить нелинейное вычисление.

Адаптивная линейная сетевая архитектура

Сеть ADALINE, показанная ниже, имеет один слой нейронов S, соединенных с входными параметрами R через матрицу весов W.

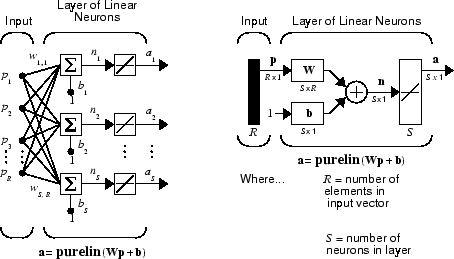
Эта сеть иногда называется MADALINE для Многих ADALINEs. Обратите внимание на то, что фигура справа задает S - выходной вектор длины a.

Правило Видроу-Хофф может только обучить одноуровневые линейные сети. Это не большая часть недостатка, однако, когда одноуровневые линейные сети так же способны как многоуровневые линейные сети. Для каждой многоуровневой линейной сети существует эквивалентная одноуровневая линейная сеть.

Один ADALINE (linearlayer)

Рассмотрите один ADALINE с двумя входными параметрами. Следующие данные показывают схему для этой сети.

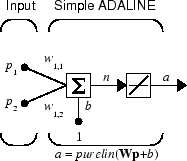
Матрица W веса в этом случае имеет только одну строку. Сетевой вывод

α = purelin (n) = purelin (Wp + b) = Wp + b

или

α = w _1,1p1 + w _1,2p2 + b

Как perceptron, ADALINE имеет контур решения, который определяется входными векторами, для которых сетевой вход n является нулем. Для n = 0 уравнение Wp + b = 0 задает такой контур решения, как показано ниже (адаптированный с благодарностью от [HDB96]).

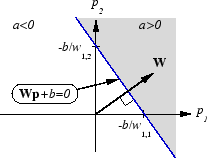
Входные векторы в верхней правой серой области приводят к выводу, больше, чем 0. Входные векторы в нижней левой белой области приводят к выводу меньше чем 0. Таким образом ADALINE может использоваться, чтобы классифицировать объекты в две категории.

Однако ADALINE может классифицировать объекты таким образом только, когда объекты линейно отделимы. Таким образом ADALINE имеет то же ограничение как perceptron.

Можно создать сеть, подобную одному показанному использованию этой команды:

net = linearlayer;
net = configure(net,[0;0],[0]);

Размеры этих двух аргументов, чтобы сконфигурировать указывают, что слой должен иметь два входных параметров и один вывод. Обычно train реализовывает эту конфигурацию для вас, но это позволяет нам осматривать веса перед обучением.

Сетевые веса и смещения обнуляются по умолчанию. Вы видите, что текущие значения используют команды:

W = net.IW{1,1}
W =
	 0	 0

b = net.b{1}
b =
	 0

Можно также присвоить произвольные значения весам и смещению, такой как 2 и 3 для весов и −4 для смещения:

net.IW{1,1} = [2 3];
net.b{1} = -4;

Можно моделировать ADALINE для конкретного входного вектора.

p = [5; 6];
a = sim(net,p)
a =
    24

Подводя итоги, можно создать сеть ADALINE с linearlayer, настроить его элементы, как вы хотите и моделируете его с sim.

Наименьшее количество среднеквадратичной погрешности

Как perceptron изучение управляет, наименьшее количество среднеквадратичной погрешности (LMS), алгоритм является примером контролируемого обучения, в котором правилу изучения предоставляют набор примеров желаемого сетевого поведения.

${p_{1}, t_{1}}, {p_{2}, t_{2}}, \dots {p_{Q}, t_{Q}}$

Здесь p_q является входом к сети, и t_q является соответствующий целевой вывод. Когда каждый вход применяется к сети, сетевой вывод сравнивается с целью. Ошибка вычисляется как различие между целевым выводом и сетевым выводом. Цель состоит в том, чтобы минимизировать среднее значение суммы этих ошибок.

$m s e = \frac{1}{Q} \sum_{k = 1}^{Q} e {(k)}^{2} = \frac{1}{Q} \sum_{k = 1}^{Q} t (k) - α (k))^{2}$

LMS-алгоритм настраивает веса и смещения ADALINE, чтобы минимизировать эту среднеквадратичную погрешность.

К счастью, индекс производительности среднеквадратичной погрешности для сети ADALINE является квадратичной функцией. Таким образом индекс производительности будет или иметь один глобальный минимум, слабый минимум или никакой минимум, в зависимости от характеристик входных векторов. А именно, характеристики входных векторов определяют, существует ли уникальное решение.

Можно узнать больше об этой теме в Главе 10 [HDB96].

LMS-алгоритм (learnwh)

Адаптивные сети будут использовать LMS-алгоритм или Видроу-Хофф, изучающего алгоритм на основе аппроксимированной процедуры быстрейшего спуска. Здесь снова, адаптивные линейные сети обучены на примерах правильного поведения.

LMS-алгоритм, показанный здесь, обсужден подробно в Линейных Нейронных сетях.

W (k + 1) = W (k) + 2αe (k) p^T (k)

b (k + 1) = b (k) + 2αe (k)

Адаптивная фильтрация (адаптируется)

Сеть ADALINE, во многом как perceptron, может только решить линейно отделимые проблемы. Это - однако, одна из наиболее широко используемых нейронных сетей, найденных в практических применениях. Адаптивная фильтрация является одной из своих областей основного приложения.

Коснувшаяся строка задержки

Вам нужен новый компонент, коснувшаяся строка задержки, чтобы полностью использовать сеть ADALINE. Такую строку задержки показывают в следующей фигуре. Входной сигнал входит слева и проходит через N-1 задержка. Выводом коснувшейся строки задержки (TDL) является N - размерный вектор, составленный из входного сигнала в текущее время, предыдущего входного сигнала, и т.д.

Адаптивный фильтр

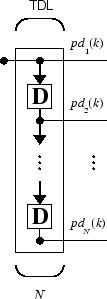
Можно объединить коснувшуюся строку задержки с сетью ADALINE, чтобы создать адаптивный фильтр, показанный в следующей фигуре.

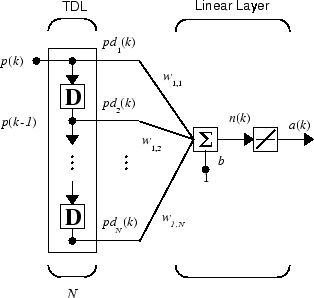
Выводом фильтра дают

$α (k) = p u r e l i n (W p + b) = \sum_{i = 1}^{R} w_{1,} {}_{i}α (k - i + 1) + b$

В цифровой обработке сигналов эта сеть упоминается как фильтр конечного импульсного ответа (FIR) [WiSt85]. Смотрите на код, используемый, чтобы сгенерировать и моделировать такую адаптивную сеть.

Адаптивный пример фильтра

Во-первых, задайте новую линейную сеть с помощью linearlayer.

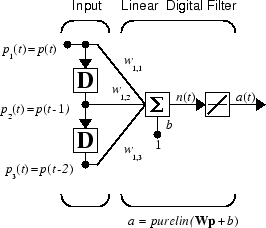
Примите, что линейный слой имеет один нейрон с одним входом и задержкой касания 0, 1, и 2 задержками.

net = linearlayer([0 1 2]);
net = configure(net,0,0);

Можно задать столько задержек, сколько вы хотите и можете не использовать некоторые значения, если вам нравится. Они должны быть в порядке возрастания.

Можно дать различные веса и значения смещения с

net.IW{1,1} = [7 8 9];
net.b{1} = [0];

Наконец, задайте начальные значения выходных параметров задержек как

pi = {1 2};

Они приказаны от левого исправиться, чтобы соответствовать задержкам, взятым сверху донизу в фигуре. Это завершает настройку сети.

Чтобы настроить вход, примите, что входные скаляры прибывают в последовательность: сначала значение 3, затем значение 4, затем значение 5, и наконец значение 6. Можно указать на эту последовательность путем определения значений как элементов массива ячеек в фигурных скобках.

p = {3 4 5 6};

Теперь, у вас есть сеть и последовательность входных параметров. Моделируйте сеть, чтобы видеть то, что ее вывод как функция времени.

[a,pf] = sim(net,p,pi)

Эта симуляция приводит к выходной последовательности

a
    [46]    [70]    [94]    [118]

и окончательные значения для задержки выходные параметры

pf
    [5]    [6]

Пример достаточно прост, что можно проверять его без калькулятора, чтобы убедиться, что вы понимаете входные параметры, начальные значения задержек, и т.д.

Сеть, только заданная, может быть обучена с функциональным adapt, чтобы произвести конкретную выходную последовательность. Предположим, например, вы хотите, чтобы сеть произвела последовательность значений 10, 20, 30, 40.

t = {10 20 30 40};

Можно обучить заданную сеть, чтобы сделать это, начинающее с начальных условий задержки, используемых выше.

Позвольте сети адаптироваться к 10, передает по данным.

for i = 1:10
    [net,y,E,pf,af] = adapt(net,p,t,pi);
end

Этот код возвращает итоговые веса, смещение и выходную последовательность, показанную сюда.

wts = net.IW{1,1}
wts =
    0.5059    3.1053    5.7046
bias = net.b{1}
bias =
   -1.5993
y
y = 
    [11.8558]    [20.7735]    [29.6679]    [39.0036]

По-видимому, если бы вы запустили дополнительные передачи, выходная последовательность была бы еще ближе к требуемым значениям 10, 20, 30, и 40.

Таким образом адаптивные сети могут быть заданы, моделированы, и наконец обучены с adapt. Однако выдающееся значение адаптивных сетей находится в их использовании, чтобы выполнить конкретную функцию, такую как прогноз или шумовая отмена.

Пример прогноза

Предположим, что вы хотите использовать адаптивный фильтр, чтобы предсказать следующее значение стационарного вероятностного процесса, p (t). Можно использовать сеть, которая, как показывают в следующей фигуре, сделала этот прогноз.

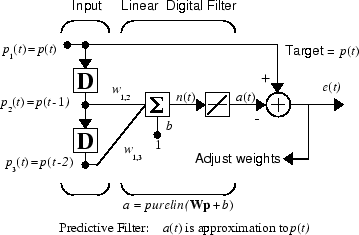
Сигнал, который будет предсказан, p (t), входит слева в коснувшуюся строку задержки. Предыдущие два значения p (t) доступны как выходные параметры от коснувшейся строки задержки. Сеть использует adapt, чтобы изменить веса на каждом временном шаге, чтобы минимизировать ошибку e (t) на ультраправом. Если эта ошибка 0, сетевой вывод a (t) точно равен p (t), и сеть сделала свой прогноз правильно.

Учитывая автокорреляционную функцию стационарного вероятностного процесса p (t), можно вычислить ошибочную поверхность, максимальный темп обучения и оптимальные значения весов. Обычно, конечно, у вас нет подробной информации о вероятностном процессе, таким образом, эти вычисления не могут быть выполнены. Это отсутствие не имеет значения для сети. После того, как это инициализируется и работа, сеть адаптируется на каждом временном шаге, чтобы минимизировать ошибку, и в относительно короткое время может предсказать вход p (t).

Глава 10 [HDB96] представляет эту проблему, проходит анализ и показывает траекторию веса во время обучения. Сеть находит оптимальные веса самостоятельно без любой трудности вообще.

Также можно попробовать пример nnd10nc, чтобы видеть адаптивный шумовой пример программы отмены в действии. Этот пример позволяет вам выбирать темп обучения и импульс (см. Многоуровневые Мелкие Нейронные сети и Обучение Обратной связи), и показывает траекторию изучения, и исходные сигналы и сигналы отмены по сравнению со временем.

Шумовой пример отмены

Рассмотрите пилота в самолете. Когда пилот говорит в микрофон, шум механизма в объединениях кабины с речевым сигналом. Этот дополнительный шум делает результирующий сигнал услышанным пассажирами низкого качества. Цель состоит в том, чтобы получить сигнал, который содержит речь пилота, но не шум механизма. Можно отменить шум с адаптивным фильтром, если вы получаете выборку шума механизма и применяете его как вход к адаптивному фильтру.

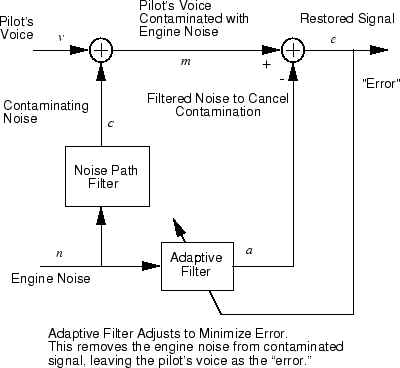
Когда предыдущие данные показывают, вы адаптивно обучаете нейронную линейную сеть, чтобы предсказать, что объединенный пилот/механизм сигнализирует, что m от механизма сигнализирует о n. Сигнал механизма n ничего не говорит адаптивной сети о речевом сигнале пилота, содержавшемся в m. Однако механизм сигнализирует, что n действительно дает сетевую информацию, которую это может использовать, чтобы предсказать, что вклад механизма в пилота/механизм сигнализирует о m.

Сеть прилагает все усилия к выводу m адаптивно. В этом случае сеть может только предсказать, что шум интерференции механизма в пилоте/механизме сигнализирует о m. Сетевая ошибка e равна m, сигналу пилота/механизма, минус предсказанный сигнал шума механизма загрязнения. Таким образом e содержит только речь пилота. Линейная адаптивная сеть адаптивно учится отменять шум механизма.

Такая адаптивная шумовая отмена обычно делает лучшее задание, чем классический фильтр, потому что она вычитает из сигнала вместо того, чтобы фильтровать его шум m сигнала.

Попробуйте demolin8 за пример адаптивной шумовой отмены.

Несколько нейрон адаптивные фильтры

Вы можете хотеть использовать больше чем один нейрон в адаптивной системе, таким образом, вам нужно некоторое дополнительное обозначение. Можно использовать коснувшуюся строку задержки с S линейные нейроны, как показано в следующей фигуре.

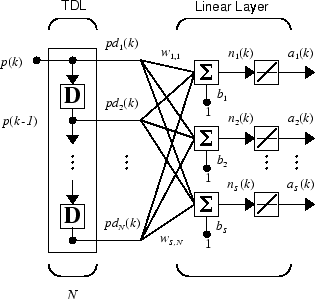
Также можно представлять эту ту же сеть в сокращенной форме.

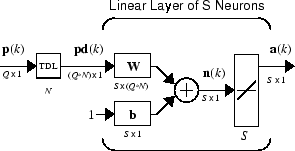
Если вы хотите показать больше детали коснувшейся строки задержки — и нет слишком многих задержек — можно использовать следующее обозначение:

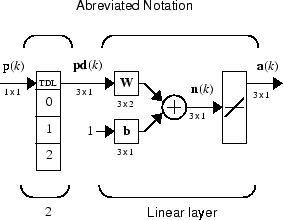
Здесь, коснувшаяся строка задержки отправляет к матрице веса:

Текущий сигнал
Предыдущий сигнал
Сигнал задержан перед этим

У вас мог быть более длинный список, и некоторые значения задержки могли быть не использованы при желании. Единственное требование - то, что задержки должны появляться в увеличивающемся порядке, когда они идут сверху донизу.

Документация