Линейные нейронные сети

Линейные сети, обсужденные в этом разделе, подобны perceptron, но их передаточная функция линейна, а не трудно ограничивает. Это позволяет их выходным параметрам брать любое значение, тогда как perceptron вывод ограничивается или 0 или 1. Линейные сети, как perceptron, могут только решить линейно отделимые проблемы.

Здесь вы разрабатываете линейную сеть, которая, когда подарено набор данных входных векторов, производит выходные параметры соответствующих целевых векторов. Для каждого входного вектора можно вычислить выходной вектор сети. Различием между выходным вектором и его целевым вектором является ошибка. Вы хотели бы найти значения для сетевых весов и смещаете таким образом, что сумма квадратов ошибок минимизирована или ниже определенного значения. Эта проблема управляема, потому что линейные системы имеют один ошибочный минимум. В большинстве случаев можно вычислить линейную сеть непосредственно, такой, что ее ошибка является минимумом для данных входных векторов и целевых векторов. В других случаях числовые проблемы запрещают прямое вычисление. К счастью, можно всегда обучать сеть, чтобы иметь минимальную ошибку при помощи наименьшего количества средних квадратичных (Видроу-Хофф) алгоритм.

Этот раздел вводит linearlayer, функцию, которая создает линейный слой и newlind, функция, которая разрабатывает линейный слой для определенной цели.

Модель нейрона

Линейный нейрон с входными параметрами R показывают ниже.

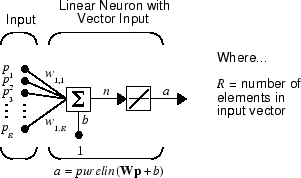
Эта сеть имеет ту же базовую структуру как perceptron. Единственная разница - то, что линейный нейрон использует линейную передаточную функцию purelin.

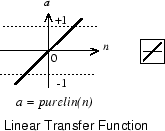
Линейная передаточная функция вычисляет, вывод нейрона путем простого возвращения значения передал ей.

$α = p u r e l i n (n) = p u r e l i n (W p + b) = W p + b$

Этот нейрон может быть обучен изучить аффинную функцию своих входных параметров или найти линейную аппроксимацию к нелинейной функции. Линейная сеть не может, конечно, быть сделана выполнить нелинейное вычисление.

Сетевая архитектура

Линейная сеть, показанная ниже, имеет один слой нейронов S, соединенных с входными параметрами R через матрицу весов W.

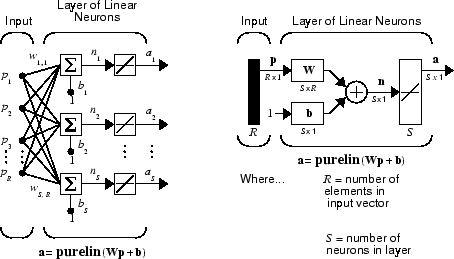
Обратите внимание на то, что фигура справа задает S - выходной вектор длины a.

Одноуровневую линейную сеть показывают. Однако эта сеть так же способна как многоуровневые линейные сети. Для каждой многоуровневой линейной сети существует эквивалентная одноуровневая линейная сеть.

Создайте линейный нейрон (linearlayer)

Рассмотрите один линейный нейрон с двумя входными параметрами. Следующие данные показывают схему для этой сети.

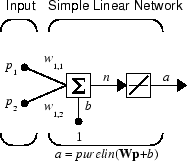
Матрица W веса в этом случае имеет только одну строку. Сетевой вывод

$α = p u r e l i n (n) = p u r e l i n (W p + b) = W p + b$

или

$α = w_{1, 1} p_{1} + w_{1, 2} p_{2} + b$

Как perceptron, линейная сеть имеет контур решения, который определяется входными векторами, для которых сетевой вход n является нулем. Для n = 0 уравнение Wp + b = 0 задает такой контур решения, как показано ниже (адаптированный с благодарностью от [HDB96]).

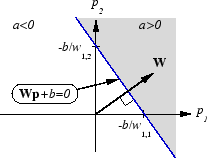
Входные векторы в верхней правой серой области приводят к выводу, больше, чем 0. Входные векторы в нижней левой белой области приводят к выводу меньше чем 0. Таким образом линейная сеть может использоваться, чтобы классифицировать объекты в две категории. Однако это может классифицировать таким образом, только если объекты линейно отделимы. Таким образом линейная сеть имеет то же ограничение как perceptron.

Можно создать эту сеть с помощью linearlayer и сконфигурировать его размерности с двумя значениями, таким образом, вход имеет два элемента, и вывод имеет тот.

net = linearlayer;
net = configure(net,[0;0],0);

Сетевые веса и смещения обнуляются по умолчанию. Вы видите текущие значения с командами

W = net.IW{1,1}
W =
     0     0

b= net.b{1}
b =
     0

Однако можно дать весам любые значения, с которыми вы хотите, такой как 2 и 3, соответственно,

net.IW{1,1} = [2 3];
W = net.IW{1,1}
W =
     2     3

Можно установить и проверять смещение таким же образом.

net.b{1} = [-4];
b = net.b{1}
b =
     -4

Можно моделировать линейную сеть для конкретного входного вектора. Попробовать

p = [5;6];

Можно найти сетевой вывод с функциональным sim.

a = net(p)
a =
    24

Подводя итоги, можно создать линейную сеть с linearlayer, настроить его элементы, как вы хотите и моделируете его с sim.

Наименьшее количество среднеквадратичной погрешности

Как perceptron изучение управляет, наименьшее количество среднеквадратичной погрешности (LMS), алгоритм является примером контролируемого обучения, в котором правилу изучения предоставляют набор примеров желаемого сетевого поведения:

${p_{1}, t_{1}}, {p_{2}, t_{2}}, \dots {p_{Q}, t_{Q}}$

Здесь pq является входом к сети, и tq является соответствующий целевой вывод. Когда каждый вход применяется к сети, сетевой вывод сравнивается с целью. Ошибка вычисляется как различие между целевым выводом и сетевым выводом. Цель состоит в том, чтобы минимизировать среднее значение суммы этих ошибок.

$m s e = \frac{1}{Q} \sum_{k = 1}^{Q} e {(k)}^{2} = \frac{1}{Q} \sum_{k = 1}^{Q} {(t (k) - α (k))}^{2}$

LMS-алгоритм настраивает веса и смещения линейной сети, чтобы минимизировать эту среднеквадратичную погрешность.

К счастью, индекс производительности среднеквадратичной погрешности для линейной сети является квадратичной функцией. Таким образом индекс производительности будет или иметь один глобальный минимум, слабый минимум или никакой минимум, в зависимости от характеристик входных векторов. А именно, характеристики входных векторов определяют, существует ли уникальное решение.

Можно найти больше об этой теме в Главе 10 [HDB96].

Проект линейной системы (newlind)

В отличие от большей части другой сетевой архитектуры, линейные сети могут быть разработаны непосредственно, если введенные/предназначаемые векторные пары известны. Можно получить определенные сетевые значения для весов и смещений, чтобы минимизировать среднеквадратичную погрешность при помощи функционального newlind.

Предположим, что входные параметры и цели

P = [1 2 3];
T= [2.0 4.1 5.9];

Теперь можно разработать сеть.

net = newlind(P,T);

Можно моделировать сетевое поведение, чтобы проверять, что проект был сделан правильно.

Y = net(P)
Y =
    2.0500    4.0000    5.9500

Обратите внимание на то, что сетевые выходные параметры вполне близко к желаемым целям.

Вы можете попробовать demolin1. Это показывает ошибочные поверхности для конкретной проблемы, иллюстрирует проект и строит разработанное решение.

Можно также использовать функциональный newlind, чтобы разработать линейные сети, имеющие задержки входа. Такие сети обсуждены в Линейных Сетях с Задержками. Во-первых, однако, задержки должны быть обсуждены.

Линейные сети с задержками

Коснувшаяся строка задержки

Вам нужен новый компонент, коснувшаяся строка задержки, чтобы полностью использовать линейную сеть. Такую строку задержки показывают ниже. Там входной сигнал входит слева и проходит через N-1 задержка. Выводом коснувшейся строки задержки (TDL) является N - размерный вектор, составленный из входного сигнала в текущее время, предыдущего входного сигнала, и т.д.

Линейный фильтр

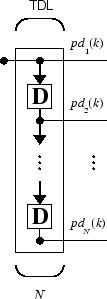
Можно объединить коснувшуюся строку задержки с линейной сетью, чтобы создать показанный линейный фильтр.

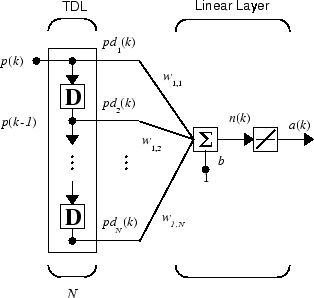
Выводом фильтра дают

$α (k) = p u r e l i n (W p + b) = \sum_{i = 1}^{R} w_{1, i} p (k - i + 1) + b$

Показанная сеть упомянута в поле цифровой обработки сигналов как фильтр конечного импульсного ответа (FIR) [WiSt85]. Посмотрите на код, используемый, чтобы сгенерировать и моделировать такую сеть.

Предположим, что вы хотите линейный слой, который выводит последовательность T, учитывая последовательность, P и две начальных входных задержки утверждают Pi.

P = {1 2 1 3 3 2};
Pi = {1 3};
T = {5 6 4 20 7 8};

Можно использовать newlind, чтобы разработать сеть с задержками, чтобы дать соответствующие выходные параметры для входных параметров. Начальная буква задержки выходные параметры предоставляется в качестве третьего аргумента, как показано ниже.

net = newlind(P,T,Pi);

Можно получить вывод разработанной сети с

Y = net(P,Pi)

дать

Y = [2.7297] [10.5405] [5.0090] [14.9550] [10.7838] [5.9820]

Как вы видите, сетевые выходные параметры не точно равны целям, но они близки, и среднеквадратичная погрешность минимизирована.

LMS-алгоритм (learnwh)

LMS-алгоритм или Видроу-Хофф, изучающий алгоритм, основан на аппроксимированной процедуре быстрейшего спуска. Здесь снова, линейные сети обучены на примерах правильного поведения.

Widrow и Hoff имели понимание, что они могли оценить среднеквадратичную погрешность при помощи квадратичной невязки в каждой итерации. Если вы берете частную производную квадратичной невязки относительно весов и смещений в k th итерация, вы имеете

$\frac{\partial e^{2} (k)}{\partial w_{1, j}} = 2 e (k) \frac{\partial e (k)}{\partial w_{1, j}}$

для j = 1,2, …, R и

$\frac{\partial e^{2} (k)}{\partial b} = 2 e (k) \frac{\partial e (k)}{\partial b}$

Затем посмотрите на частную производную относительно ошибки.

$\frac{\partial e (k)}{\partial w_{1, j}} = \frac{\partial [t (k) - α (k)]}{\partial w_{1, j}} = \frac{\partial}{\partial w_{1, j}} [t (k) - (W p (k) + b)]$

или

$\frac{\partial e (k)}{\partial w_{1, j}} = \frac{\partial}{\partial w_{1, j}} [t (k) - (\sum_{i = 1}^{R} w_{1, i} p_{i} (k) + b)]$

Здесь _pi (k) является ith элементом входного вектора в kth итерации.

Это может быть упрощено до

$\frac{\partial e (k)}{\partial w_{1, j}} = - p_{j} (k)$

$\frac{\partial e (k)}{\partial b} = - 1$

Наконец, измените матрицу веса, и смещение будет

2αe (k) p (k)

2αe (k)

Эти два уравнения формируют основание Видроу-Хофф (LMS) изучение алгоритма.

Эти результаты могут быть расширены к случаю нескольких нейронов и написаны в матричной форме как

$\begin{array}{l} W (k + 1) = W (k) + 2 α e (k) p^{T} (k) \\ b (k + 1) = b (k) + 2 α e (k) \end{array}$

Здесь ошибка e и смещение b являются векторами, и α является темпом обучения. Если α является большим, изучение происходит быстро, но если это является слишком большим, это может привести к нестабильности, и ошибки могут даже увеличиться. Чтобы гарантировать стабильное изучение, темп обучения должен быть меньше, чем обратная величина самого большого собственного значения корреляционной матрицы pTp входных векторов.

Вы можете хотеть считать часть Главы 10 [HDB96] для получения дополнительной информации о LMS-алгоритме и его сходимости.

К счастью, существует функция тулбокса, learnwh, который делает все вычисление для вас. Это вычисляет изменение в весах как

dw = lr*e*p'

и смещение изменяется как

db = lr*e

Постоянные 2, показанные несколько строк выше, были поглощены в темп обучения кода lr. Функциональный maxlinlr вычисляет этот максимальный стабильный темп обучения lr как 0,999 * P' *P.

Введите help learnwh и help maxlinlr для получения дополнительной информации об этих двух функциях.

Линейная классификация (train)

Линейные сети могут быть обучены, чтобы выполнить линейную классификацию с функциональным train. Эта функция применяет каждый вектор набора входных векторов и вычисляет сетевой вес, и смещение постепенно увеличивается из-за каждых из входных параметров согласно learnp. Затем сеть настроена с суммой всех этих исправлений. Каждый проходит через входные векторы, называется эпохой. Это контрастирует с adapt, который настраивает веса для каждого входного вектора, когда это представлено.

Наконец, train применяет входные параметры к новой сети, вычисляет выходные параметры, сравнивает их со связанными целями и вычисляет среднеквадратичную погрешность. Если ошибочной цели удовлетворяют, или если максимальное количество эпох достигнуто, обучение останавливается, и train возвращает новую сеть и учебную запись. В противном случае train проходит другую эпоху. К счастью, LMS-алгоритм сходится, когда эта процедура выполняется.

Простая проблема иллюстрирует эту процедуру. Считайте линейную сеть введенной ранее.

Предположим, что у вас есть следующая проблема классификации.

${p_{1} = [\begin{array}{l} 22 \end{array}], t_{1} = 0} {p_{2} = [\begin{matrix} 1 \\ - 2 \end{matrix}], t_{2} = 1} {p_{3} = [\begin{matrix} - \\ 22 \end{matrix}], t_{3} = 0} {p_{4} = [\begin{matrix} - \\ 11 \end{matrix}], t_{4} = 1}$

Здесь существует четыре входных вектора, и вы хотите сеть, которая производит вывод, соответствующий каждому входному вектору, когда тот вектор представлен.

Используйте train, чтобы получить веса и смещения для сети, которая производит правильные цели для каждого входного вектора. Начальные веса и смещение для новой сети 0 по умолчанию. Установите ошибочную цель к 0,1, а не примите ее значение по умолчанию 0.

P = [2 1 -2 -1;2 -2 2 1];
T = [0 1 0 1];
net = linearlayer;
net.trainParam.goal= 0.1;
net = train(net,P,T);

Проблема запускается в течение 64 эпох, достигая среднеквадратичной погрешности 0,0999. Новые веса и смещение

weights = net.iw{1,1}
weights =
   -0.0615   -0.2194
bias = net.b(1)
bias =
    [0.5899]

Можно моделировать новую сеть как показано ниже.

A = net(P)
A =
    0.0282    0.9672    0.2741    0.4320

Можно также вычислить ошибку.

err = T - sim(net,P)
err =
   -0.0282    0.0328   -0.2741    0.5680

Обратите внимание на то, что цели не поняты точно. Проблема запустилась бы дольше в попытке добраться, совершенные результаты имели меньшую ошибочную цель, выбранный, но в этой проблеме не возможно получить цель 0. Сеть ограничивается в ее возможности. Смотрите Ограничения и Предостережения для примеров различных ограничений.

Этот пример программы, demolin2, показывает обучение линейного нейрона и строит траекторию веса и ошибку во время обучения.

Вы можете также попытаться запустить пример программы nnd10lc. Это решает классику и исторически интересную проблему, показывает, как сеть может быть обучена, чтобы классифицировать различные шаблоны и показывает, как обучивший сеть отвечает, когда шумные шаблоны представлены.

Ограничения и предостережения

Линейные сети могут только изучить линейные соотношения между векторами ввода и вывода. Таким образом они не могут найти решения некоторых проблем. Однако, даже если идеальное решение не будет существовать, линейная сеть минимизирует сумму квадратичных невязок, если темп обучения lr будет достаточно небольшим. Сеть найдет столь близкое решение, как возможно, учитывая линейную природу архитектуры сети. Это свойство содержит, потому что ошибочная поверхность линейной сети является многомерной параболой. Поскольку параболы имеют только один минимум, алгоритм спуска градиента (такой как правило LMS) должен произвести решение в том минимуме.

Линейные сети имеют различные другие ограничения. Некоторые из них обсуждены ниже.

Сверхрешительные системы

Рассмотрите сверхрешительную систему. Предположим, что у вас есть сеть, которая будет обучена с четырьмя входными векторами с одним элементом и четырьмя целями. Идеальное решение wp + b = t для каждых из входных параметров не может существовать, поскольку существует четыре уравнения ограничения, и только один вес и одно смещение, чтобы настроить. Однако правило LMS все еще минимизирует ошибку. Вы можете попробовать demolin4, чтобы видеть, как это сделано.

Недоопределенные системы

Рассмотрите один линейный нейрон с одним входом. На этот раз, в demolin5, обучите его только на одном входном векторе с одним элементом и его целевом векторе с одним элементом:

P = [1.0];
T = [0.5];

Обратите внимание на то, что, в то время как существует только одно ограничение, являющееся результатом одной пары входа/цели, существует две переменные, вес и смещение. Наличие большего количества переменных, чем ограничения приводит к недоопределенной проблеме с бесконечным числом решений. Можно попробовать demolin5, чтобы исследовать эту тему.

Линейно зависимые векторы

Обычно это - прямое задание, чтобы определить, может ли линейная сеть решить проблему. Обычно, если линейная сеть имеет, по крайней мере, как много степеней свободы (S *R + S = количество весов и смещений) как ограничения (Q = пары векторов входа/цели), то сеть может решить проблему. Это верно кроме тех случаев, когда входные векторы линейно зависят, и они применяются к сети без смещений. В этом случае, как показано с примером demolin6, сеть не может решить проблему с нулевой ошибкой. Вы можете хотеть попробовать demolin6.

Слишком Большой темп обучения

Можно всегда обучать линейную сеть с правилом Видроу-Хофф найти минимальное ошибочное решение для его весов и смещений, пока темп обучения является достаточно небольшим. demolin7 в качестве примера показывает то, что происходит, когда нейрон с одним входом и смещением обучен с темпом обучения, больше, чем рекомендуемый maxlinlr. Сеть обучена с двумя различными темпами обучения, чтобы показать результаты использования слишком большого темпа обучения.

Документация