Основной стандартный блок для нейронных сетей является нейроном одно входа, таким как этот пример.
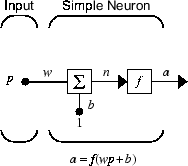
Существует три отличных функциональных операции, которые происходят в этом нейроне в качестве примера. Во-первых, скалярный вход p умножается на скалярный вес w, чтобы сформировать продукт wp, снова скаляр. Во-вторых, взвешенный вход wp добавляется к скалярному смещению b, чтобы сформировать сетевой вход n. (В этом случае можно просмотреть смещение как сдвиг функционального f налево суммой b. Смещение во многом как вес, за исключением того, что оно имеет постоянный вход 1.) Наконец, сетевой вход передается через передаточную функцию f, который производит скалярный вывод a. Имена, данные этим трем процессам: функция веса, сетевая функция ввода и передаточная функция.
Для многих типов нейронных сетей функция веса является продуктом веса времена вход, но другие функции веса (например, расстояние между весом и входом, |w − p |) иногда используются. (Для списка функций веса введите help nnweight.) Наиболее распространенная сетевая функция ввода является суммированием взвешенных входных параметров со смещением, но другие операции, такие как умножение, могут использоваться. (Для списка сетевых функций ввода введите help nnnetinput.) Введение в Радиальные Базисные Нейронные сети обсуждает, как расстояние может использоваться в качестве функции веса, и умножение может использоваться в качестве сетевой функции ввода. Существует также много типов передаточных функций. Примеры различных передаточных функций находятся в Передаточных функциях. (Для списка передаточных функций введите help nntransfer.)
Обратите внимание на то, что w и b являются оба корректируемыми скалярными параметрами нейрона. Центральная идея нейронных сетей состоит в том, что такие параметры могут быть настроены так, чтобы сеть показала некоторое желаемое или интересное поведение. Таким образом можно обучить сеть, чтобы сделать конкретное задание путем корректировки параметров смещения или веса.
Все нейроны в программном обеспечении Deep Learning Toolbox™ имеют условие для смещения, и смещение используется во многих примерах и принято в большей части этого тулбокса. Однако можно не использовать смещение в нейроне, если вы хотите.
Много передаточных функций включены в программное обеспечение Deep Learning Toolbox.
Две из обычно используемых функций показывают ниже.
Следующая фигура иллюстрирует линейную передаточную функцию.
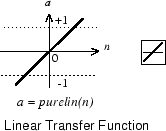
Нейроны этого типа используются в последнем слое многоуровневых сетей, которые используются в качестве функции approximators. Это показывают в Многоуровневых Мелких Нейронных сетях и Обучении Обратной связи.
Сигмоидальная передаточная функция, показанная ниже взятий вход, который может иметь любое значение между плюс и минус бесконечность и давит вывод в область значений от 0 до 1.
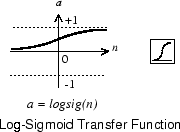
Эта передаточная функция обычно используется в скрытых слоях многоуровневых сетей, частично потому что это дифференцируемо.
Символ в квадрате справа от каждого графика передаточной функции, показанного выше, представляет связанную передаточную функцию. Эти значки заменяют общий f в блоках сетевого графика, чтобы показать конкретную используемую передаточную функцию.
Для полного списка передаточных функций введите help nntransfer. Можно также задать собственные передаточные функции.
Можно экспериментировать с простым нейроном и различными передаточными функциями путем выполнения примера программы nnd2n1.
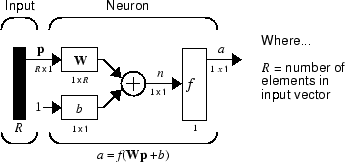
Простой нейрон может быть расширен, чтобы обработать входные параметры, которые являются векторами. Нейрон с одним R - входной вектор элемента показывают ниже. Здесь отдельные входные элементы
умножаются на веса
и взвешенные значения питаются соединение подведения итогов. Их суммой является просто Wp, скалярное произведение (одна строка) матрица W и вектор p. (Существуют другие функции веса, в дополнение к скалярному произведению, такие как расстояние между строкой матрицы веса и входным вектором, как во Введении в Радиальные Базисные Нейронные сети.)
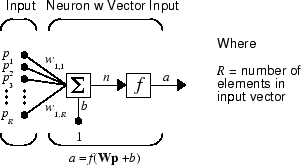
Нейрон имеет смещение b, который суммирован со взвешенными входными параметрами, чтобы сформировать сетевой вход n. (В дополнение к суммированию другие сетевые функции ввода могут использоваться, такие как умножение, которое используется во Введении в Радиальные Базисные Нейронные сети.) Сетевой вход n является аргументом передаточной функции f.
Это выражение может, конечно, быть написано в коде MATLAB® как
n = W*p + b
Однако вы редко будете написанием кода на этом уровне, поскольку такой код уже встроен в функции, чтобы задать и моделировать целые сети.
Фигура одного нейрона, показанного выше, содержит много детали. Когда вы рассматриваете сети со многими нейронами, и возможно слои многих нейронов, существует так много детали, что основные мысли имеют тенденцию быть потерянными. Таким образом авторы создали сокращенное обозначение для отдельного нейрона. Это обозначение, которое используется позже в схемах нескольких нейронов, показывают здесь.
Здесь входной вектор p представлен твердой темной вертикальной панелью слева. Размерности p показывают ниже символа p в фигуре как R × 1. (Обратите внимание на то, что прописная буква, такая как R в предыдущем предложении, используется при обращении к размеру вектора.) Таким образом p является вектором элементов входа R. Эти входные параметры постумножают одну строку, R - матрица W столбца. Как прежде, постоянный 1 вводит нейрон как вход и умножается на скалярное смещение b. Сетевым входом к передаточной функции f является n, сумма смещения b и продукт Wp. Эта сумма передается передаточной функции f, чтобы получить вывод a нейрона, который в этом случае является скаляром. Обратите внимание на то, что, если бы был больше чем один нейрон, сетевой вывод был бы вектором.
Слой сети задан в предыдущей фигуре. Слой включает веса, операции умножения и подведения итогов (здесь реализованный как векторное произведение Wp), смещение b и передаточная функция f. Массив входных параметров, вектор p, не включен в или вызвал слой.
Как с Простым Нейроном, существует три операции, которые происходят в слое: функция веса (умножение матриц или скалярное произведение, в этом случае), сетевая функция ввода (суммирование, в этом случае), и передаточная функция.
Каждый раз, когда это сокращенное сетевое обозначение используется, размеры матриц показывают чуть ниже их матричных имен переменных. Это обозначение позволит вам понимать архитектуру и следовать за матричной математикой, сопоставленной с ними.
Как обсуждено в Передаточных функциях, когда определенная передаточная функция должна использоваться в фигуре, символ для той передаточной функции заменяет f, показанный выше. Вот некоторые примеры.

Можно экспериментировать с двухэлементным нейроном путем выполнения примера программы nnd2n2.