Документация

Модель нейрона

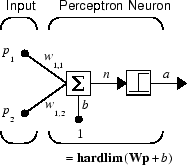
perceptron нейрон, который использует передаточную функцию жесткого предела hardlim, показывают ниже.

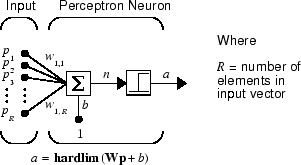
Каждый внешний вход взвешивается с соответствующим весом w _1j, и сумма взвешенных входных параметров отправляется в передаточную функцию жесткого предела, которая также имеет вход 1 переданного к нему посредством смещения. Передаточную функцию жесткого предела, которая возвращает 0 или 1, показывают ниже.

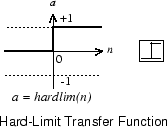
perceptron нейрон производит 1, если сетевой вход в передаточную функцию равен или больше, чем 0; в противном случае это производит 0.

Передаточная функция жесткого предела дает perceptron способность классифицировать входные векторы путем деления входного пробела на две области. А именно, выходные параметры будут 0, если сетевой вход n будет меньше чем 0, или 1, если сетевой вход n 0 или больше. Следующие данные показывают входной пробел 2D входного нейрона жесткого предела с весами w _1,1 = −1, w _1,2 = 1 и смещение b = 1.

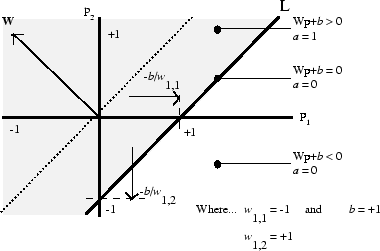
Две области классификации формируются границей решения L в
Wp + b = 0. Эта строка перпендикулярна матрице W веса и переключенная согласно смещению b. Входные векторы выше и слева от строки L приведут к сетевому входу, больше, чем 0 и, поэтому, заставят нейрон жесткого предела выводить 1. Входные векторы ниже и справа от строки L заставляют нейрон выводить 0. Можно выбрать вес и сместить значения, чтобы ориентировать и переместить разделительную линию, чтобы классифицировать входной пробел, как желаемый.

Нейроны жесткого предела без смещения будут всегда иметь строку классификации, проходящую источник. Добавление смещения позволяет нейрону решать проблемы, где два набора входных векторов не расположены на различных сторонах источника. Смещение позволяет контуру решения быть отказанным от источника, как показано в графике выше.

Вы можете хотеть запустить пример программы nnd4db. С ним можно переместить контур решения вокруг, выбрать новые входные параметры, чтобы классифицировать, и видеть, как повторное приложение правила изучения приводит к сети, которая действительно классифицирует входные векторы правильно.

Архитектура Perceptron

perceptron сеть состоит из единственного слоя S perceptron нейроны, соединенные с входными параметрами R через набор весов _wi,j, как показано ниже в двух формах. Как прежде, сетевые индексы i и j указывают, что _wi,j является силой связи от j th вход к i th нейрон.

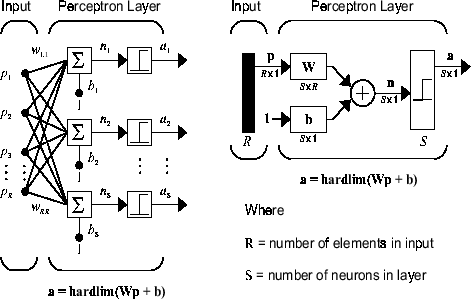
perceptron изучение правила, описанного вскоре, способен к обучению только единственный слой. Таким образом только сети с одним слоем рассматриваются здесь. Это ограничение ограничения мест на вычисление perceptron может выполнить. Типы проблем, что perceptrons способны к решению, обсуждены в Ограничениях и Предостережениях.

Создайте Perceptron

Можно создать perceptron со следующим:

net = perceptron;
net = configure(net,P,T);

где входные параметры следующие:

Обычно функция hardlim используется в perceptrons, таким образом, это - значение по умолчанию.

Следующие команды создают perceptron сеть с одним входным вектором с одним элементом со значениями 0 и 2, и один нейрон с выходными параметрами, которые могут быть или 0 или 1:

P = [0 2];
T = [0 1];
net = perceptron;
net = configure(net,P,T);

Вы видите, какая сеть была создана путем выполнения следующей команды:

inputweights = net.inputweights{1,1}

который уступает

inputweights = 
        delays: 0
       initFcn: 'initzero'
         learn: true
      learnFcn: 'learnp'
    learnParam: (none)
          size: [1 1]
     weightFcn: 'dotprod'
   weightParam: (none)
      userdata: (your custom info)

Функцией изучения значения по умолчанию является learnp, который обсужден в Perceptron Изучение Правила (learnp). Сетевым входом к передаточной функции hardlim является dotprod, который генерирует продукт входного вектора и матрицы веса и добавляет смещение, чтобы вычислить сетевой вход.

Функция инициализации по умолчанию initzero используется, чтобы обнулить начальные значения весов.

Точно так же

biases = net.biases{1}

дает

biases = 
       initFcn: 'initzero'
         learn: 1
      learnFcn: 'learnp'
    learnParam: []
          size: 1
      userdata: [1x1 struct]

Вы видите, что инициализация по умолчанию для смещения также 0.

Perceptron изучение правила (learnp)

Perceptrons обучены на примерах желаемого поведения. Желаемое поведение может быть получено в итоге набором входа, выведите пары

где p является входом к сети, и t является соответствующий правильный (целевой) вывод. Цель состоит в том, чтобы уменьшать ошибку e, который является различием t − между ответом нейрона a и целевым вектором t. perceptron изучение правила learnp вычисляет желаемые изменения в весах и смещениях perceptron, учитывая входной вектор p и связанную ошибку e. Целевой вектор t должен содержать значения или 0 или 1, потому что perceptrons (с передаточными функциями hardlim) может только вывести эти значения.

Каждый раз, когда learnp выполняется, perceptron имеет лучший шанс создания правильных выходных параметров. Правило perceptron, как доказывают, сходится на решении в конечном числе итераций, если решение существует.

Если смещение не используется, learnp работает, чтобы найти решение путем изменения только вектора веса w, чтобы указать на входные векторы, которые будут классифицированы как 1 и далеко от векторов, которые будут классифицированы как 0. Это приводит к контуру решения, который перпендикулярен w, и это правильно классифицирует входные векторы.

Существует три условия, которые могут произойти для одного нейрона, если входной вектор p представлен и ответ сети расчетного:

СЛУЧАЙ 1. Если входной вектор представлен, и вывод нейрона правилен (= t и e = t – = 0), то вектор веса w не изменен.

СЛУЧАЙ 2. Если нейрон вывел, 0 и должен был быть 1 (= 0 и t = 1, и e = t – = 1), входной вектор p добавляется к вектору веса w. Это высказывает мнение вектора веса ближе к входному вектору, увеличивая шанс, что входной вектор будет классифицирован как 1 в будущем.

СЛУЧАЙ 3. Если нейрон вывел, 1 и должен был быть 0 (= 1 и t = 0, и e = t – = –1), входной вектор p вычтен из вектора веса w. Это высказывает мнение вектора веса дальше от входного вектора, увеличивая шанс, что входной вектор будет классифицирован как 0 в будущем.

perceptron изучение правила может быть записан более кратко с точки зрения ошибки e = t – a и изменение, которое будет сделано к вектору веса Δw:

СЛУЧАЙ 1. Если e = 0, то делайте изменение Δw равным 0.

СЛУЧАЙ 2. Если e = 1, то делайте изменение Δw равным pT.

СЛУЧАЙ 3. Если e = –1, то делайте изменение Δw равным –pT.

Все три случая могут затем быть записаны с отдельным выражением:

Можно получить выражение для изменений в смещении нейрона путем отмечания, что смещение является просто весом, который всегда имеет вход 1:

Для случая слоя нейронов вы имеете

и

perceptron изучение правила может быть получен в итоге можно следующим образом:

и

где e = t – a.

Теперь попробуйте простой пример. Запустите с одного нейрона, имеющего входной вектор со всего двумя элементами.

net = perceptron;
net = configure(net,[0;0],0);

Кроме того установите смещение, равное 0 и веса к 1 и-0.8:

net.b{1} =  [0];
w = [1 -0.8];
net.IW{1,1} = w;

Входной целевой парой дают

p = [1; 2];
t = [1];

Можно вычислить вывод и ошибку с

a = net(p)
a =
     0
e = t-a
e =
     1

и используйте функциональный learnp, чтобы найти изменение в весах.

dw = learnp(w,p,[],[],[],[],e,[],[],[],[],[])
dw =
     1     2

Новые веса, затем, получены как

w = w + dw
w =
    2.0000    1.2000

Процесс нахождения новых весов (и смещения) может быть повторен, пока нет никаких ошибок. Вспомните, что perceptron, изучение правила, как гарантируют, будет сходиться в конечном числе шагов для всех проблем, которые могут быть решены perceptron. Они включают все проблемы классификации, которые линейно отделимы. Объекты, которые будут классифицированы на такие случаи, могут быть разделены одной строкой.

Вы можете хотеть попробовать пример nnd4pr. Это позволяет вам выбирать новые входные векторы и применять правило изучения классифицировать их.

Обучение (train)

Если sim и learnp будут использоваться неоднократно, чтобы представить входные параметры perceptron и изменить perceptron веса и смещения согласно ошибке, perceptron в конечном счете найдет вес и сместит значения, которые решают проблему, учитывая, что perceptron может решить его. Каждый обход через весь учебный вход и целевые векторы называется передачей.

Функциональный train выполняет такой цикл вычисления. В каждой передаче функциональные доходы train через заданную последовательность входных параметров, вычисляя вывод, ошибку и сетевую корректировку к каждому входному вектору в последовательности, когда представлены входные параметры.

Обратите внимание на то, что train не гарантирует, что получившаяся сеть делает свое задание. Необходимо проверять новые значения W и b путем вычисления сетевого вывода для каждого входного вектора, чтобы видеть, достигнуты ли все цели. Если сеть не выполняет успешно, можно обучить ее далее путем вызова train снова с новыми весами и смещениями для большего количества учебных передач, или можно анализировать проблему видеть, является ли это подходящая проблема для perceptron. Проблемы, которые не могут быть решены perceptron сетью, обсуждены в Ограничениях и Предостережениях.

Чтобы проиллюстрировать метод обучения, работайте через простую проблему. Рассмотрите один нейрон perceptron с одним векторным входом, имеющим два элемента:

Эта сеть и проблема, которую вы собираетесь рассмотреть, достаточно просты, что можно выполнить то, что сделано с ручными вычислениями, если вы хотите. Проблема, обсужденная ниже, следует, это нашло в [HDB1996].

Предположим, что вы имеете следующую проблему классификации и хотели бы решить ее с одним векторным входом, двухэлементной perceptron сетью.

Используйте начальные веса и смещение. Обозначьте переменные на каждом шаге этого вычисления при помощи номера в круглых скобках после переменной. Таким образом, выше, начальные значения являются W (0) и b (0).

Запустите путем вычисления вывода a perceptron для первого входного вектора p1, использования начальных весов и смещения.

Вывод a не равняется целевому значению t ₁, поэтому использует perceptron правило, чтобы найти инкрементные изменения в весах и смещениях на основе ошибки.

Можно вычислить новые веса и смещение, использующее правила обновления perceptron.

Теперь представьте следующий входной вектор, p2. Вывод вычисляется ниже.

В этом случае цель равняется 1, таким образом, ошибка является нулем. Таким образом нет никаких изменений в весах или смещении, таким образом, W (2) = W (1) = [−2 −2] и b (2) = b (1) = −1.

Можно продолжить этим способом, представив p3 затем, вычислив вывод и ошибку, и внеся изменения в весах и смещении, и т.д. После создания одной передачи через все четыре входных параметров вы получаете значения W (4) = [−3 −1] и b (4) = 0. Чтобы определить, получено ли удовлетворительное решение, сделайте одну передачу через все входные векторы, чтобы видеть, производят ли они все желаемые целевые значения. Это не верно для четвертого входа, но алгоритм действительно сходится на шестом представлении входа. Окончательные значения

Это завершает ручное вычисление. Теперь, как можно сделать это использование функции train?

Следующий код задает perceptron.

net = perceptron;

Рассмотрите заявление одного входа

p = [2; 2];

наличие цели

t = [0];

Установите epochs на 1, так, чтобы train прошел входные векторы (только один здесь) всего одно время.

net.trainParam.epochs = 1;
net = train(net,p,t);

Новые веса и смещение

w = net.iw{1,1}, b = net.b{1}
w =
    -2    -2
b =
    -1

Таким образом начальные веса и смещение 0, и после обучения только на первом векторе, у них есть значения [−2 −2] и −1, так же, как вы вручаете вычисленный.

Теперь примените второй входной вектор p2. Вывод равняется 1, как это будет, пока веса и смещение не изменяются, но теперь цель равняется 1, ошибка будет 0, и изменение будет нулем. Вы могли продолжить таким образом, начинающий с предыдущего результата и применяющий новый входной вектор раз за разом. Но можно сделать это задание автоматически с train.

Примените train в течение одной эпохи, одной передачи через последовательность всех четырех входных векторов. Запустите с сетевого определения.

net = perceptron;
net.trainParam.epochs = 1;

Входные векторы и цели

p = [[2;2] [1;-2] [-2;2] [-1;1]]
t = [0 1 0 1]

Теперь обучите сеть с

net = train(net,p,t);

Новые веса и смещение

w = net.iw{1,1}, b = net.b{1}
w =
    -3    -1
b =
     0

Это - тот же результат, как вы добрались ранее вручную.

Наконец, моделируйте обучивший сеть для каждых из входных параметров.

a = net(p)
a = 
      0     0     1     1

Выходные параметры еще не равняются целям, таким образом, необходимо обучить сеть больше чем для одной передачи. Попробуйте больше эпох. Это выполнение дает среднюю производительность абсолютной погрешности 0 после двух эпох:

net.trainParam.epochs = 1000;
net = train(net,p,t);

Таким образом сеть была обучена к тому времени, когда входные параметры были представлены на третьей эпохе. (Как вы знаете от ручного вычисления, сеть сходится на представлении шестого входного вектора. Это происходит в середине второй эпохи, но требуется третья эпоха, чтобы обнаружить сетевую конвергенцию.) Итоговые веса и смещение

w = net.iw{1,1}, b = net.b{1}
w =
    -2    -3
b =
     1

Моделируемый вывод и ошибки для различных входных параметров

a = net(p)
a =
             0             1             0             1
error = a-t
error =
             0             0             0             0

Вы подтверждаете, что метод обучения успешен. Сеть сходится и производит правильные целевые выходные параметры для этих четырех входных векторов.

Учебной функцией по умолчанию для сетей, созданных с perceptron, является trainc. (Можно найти это путем выполнения net.trainFcn.) Эта учебная функция применяет perceptron изучение правила в его чистой форме, в тот, отдельные входные векторы применяются индивидуально в последовательности, и исправления к весам и смещение сделаны после каждого представления входного вектора. Таким образом, perceptron обучение с train будет сходиться в конечном числе шагов, если представленная проблема не может быть решена с простым perceptron.

Функциональный train может использоваться в различных способах другими сетями также. Введите help train, чтобы читать больше об этой основной функции.

Вы можете хотеть попробовать различные примеры программы. Например, demop1 иллюстрирует классификацию и обучение простого perceptron.

Ограничения и предостережения

Сети Perceptron должны быть обучены с adapt, который представляет входные векторы сети по одному и делает исправления к сети на основе результатов каждого представления. Использование adapt таким образом гарантирует, что любая линейно отделимая проблема решена в конечном числе учебных презентаций.

Как отмечено в предыдущих страницах, perceptrons может также быть обучен с функциональным train. Обычно, когда train используется для perceptrons, он представляет входные параметры сети в пакетах и делает исправления к сети на основе суммы всех отдельных исправлений. К сожалению, нет никакого доказательства, что такой учебный алгоритм сходится для perceptrons. На той учетной записи не рекомендуется использование train для perceptrons.

Сети Perceptron имеют несколько ограничений. Во-первых, выходные значения perceptron могут взять только одно из двух значений (0 или 1) из-за передаточной функции жесткого предела. Во-вторых, perceptrons может только классифицировать линейно отделимые наборы векторов. Если прямая линия или плоскость могут чертиться, чтобы разделить входные векторы на их правильные категории, входные векторы линейно отделимы. Если векторы не будут линейно отделимы, изучение никогда не будет достигать точки, где все векторы классифицируются правильно. Однако было доказано, что, если векторы линейно отделимы, perceptrons обученный адаптивно, будет всегда находить решение в конечный промежуток времени. Вы можете хотеть попробовать demop6. Это показывает трудность попытки классифицировать входные векторы, которые не линейно отделимы.

Только справедливо, однако, указать, что сети больше чем с одним perceptron могут использоваться, чтобы решить более трудные проблемы. Например, предположите, что у вас есть набор четырех векторов, которые требуется классифицировать в отличные группы, и что две линии могут быть проведены, чтобы разделить их. Сеть 2D нейрона может быть найдена такой, что ее два контура решения классифицируют входные параметры в четыре категории. Для дополнительной дискуссии о perceptrons и исследовать более комплексные perceptron проблемы, см. [HDB1996].