Цифровые преобразования частоты

Детали и методология

Обзор преобразований
Выберите Features Subject to Transformation
Отображение от прототипного фильтра, чтобы предназначаться для фильтра
Сводные данные преобразований частоты

Обзор преобразований

Преобразование существующего КИХ или БИХ-проектов фильтра к измененной БИХ-форме часто делается с помощью allpass преобразования частоты. Несмотря на то, что получившиеся проекты могут быть значительно более дорогими с точки зрения размерности, чем прототип (исходный) фильтр, их простота использования в фиксированных или переменных приложениях является большим преимуществом.

Общее представление о преобразовании частоты состоит в том, чтобы взять существующий прототипный фильтр и произвести другой фильтр из него, который сохраняет некоторые характеристики прототипа в частотном диапазоне. Функции преобразования достигают этого, заменяя каждый элемент задержки прототипного фильтра с фильтром allpass, тщательно разработанным, чтобы иметь предписанную характеристику фазы для достижения модификаций, которые требует разработчик.

Каноническая форма отображения обычно используемого

$H_{T} (z) = H_{o} [H_{A} (z)]$

_HA (z) является th-порядком N allpass сопоставляющий фильтр, данный

$\begin{array}{l} H_{A} (z) = S \frac{\sum_{i = 0}^{N} α_{i} z^{- i}}{\sum_{i = 0}^{N} α_{i} z^{- N + i}} = \frac{N_{A} (z)}{D_{A} (z)} \\ α_{0} = 1 \end{array}$

где

_Ho (z) — Передаточная функция прототипного фильтра

_HA (z) — Передаточная функция allpass, сопоставляющего фильтр

_HT (z) — Передаточная функция целевого фильтра

Давайте посмотрим на простой пример преобразования, данного

$H_{T} (z) = H_{o} (- z)$

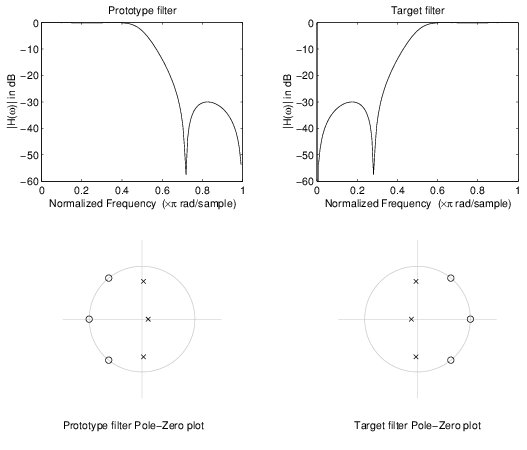
Целевой фильтр имеет свои полюса и обнуляет инвертированный через источник вещественных и мнимых осей. Для действительного прототипа фильтра это дает зеркальный эффект против 0,5, что означает, что lowpass _Ho (z) дает начало действительному highpass _HT (z). Это показывают в следующей фигуре для прототипного фильтра, разработанного как полуполоса третьего порядка эллиптический фильтр.

Пример простого зеркального преобразования

Выбор фильтра allpass обеспечить отображение частоты необходим, чтобы обеспечить, перевод частоты прототипа фильтруют частотную характеристику на целевой фильтр, меняя положение частоты функций от прототипного фильтра, не влияя на полную форму ответа фильтра.

Фазовый отклик фильтра отображения, нормированного к π, может быть интерпретирован как функция перевода:

$H (w_{n e w}) = ω_{o l d}$

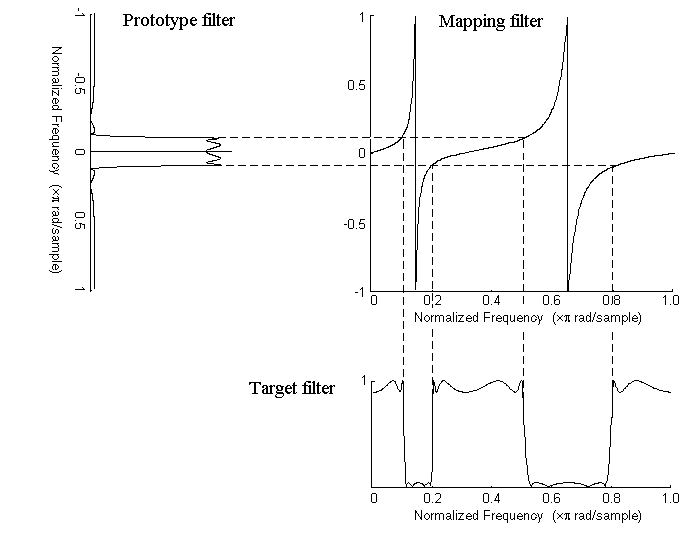
Графическую интерпретацию преобразования частоты показывают в фигуре ниже. Комплексное многополосное преобразование берет действительный фильтр lowpass и преобразовывает его во многие полосы пропускания вокруг модульного круга.

Графическая интерпретация процесса отображения

Большинство преобразований частоты основано на allpass второго порядка, сопоставляющем фильтр:

$H_{A} (z) = \pm \frac{1 + α_{1} z^{- 1} + α_{2} z^{- 2}}{α_{2} + α_{1} z^{- 1} + z^{- 2}}$

Эти две степени свободы, обеспеченные _α1 и выбором _α2, не полностью используются обычным строгим набором “стрижки под ежика” классические отображения как lowpass к полосе пропускания. Вместо этого любые две функции передаточной функции могут быть перемещены (почти) на любые два других места частоты, если _α1 и _α2 выбраны, чтобы сохранить полюса _HA (z) строго вне модульного круга (поскольку _HA (z) заменяют z в прототипной передаточной функции). Кроме того, как сначала указано Constantinides, выбор внешнего знака влияет, может ли исходная функция в нуле быть перемещена (знак "минус", условие, известное как “мобильность DC”) или может ли частота Найквиста быть перемещена (“возникновение случая” мобильности Найквиста, когда ведущий знак положителен).

Выберите Features Subject to Transformation

Выбор соответствующего преобразования частоты для достижения необходимого эффекта и правильных функций прототипного фильтра очень важен и нуждается во внимательном рассмотрении. Не желательно использовать преобразование первого порядка для управления больше чем одной функцией. Фильтр отображения не даст достаточно гибкости. Также не хорошо использовать преобразование высшего порядка только, чтобы изменить частоту среза фильтра lowpass. Увеличение порядка фильтра было бы слишком большим, не рассматривая дополнительную копию прототипного фильтра, который может быть создан в нежелательных местах.

Покажите выбор для действительного Lowpass к полосовому преобразованию

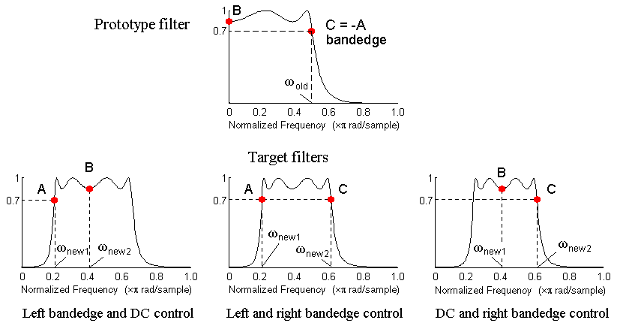
Чтобы проиллюстрировать идею, действительное многоточечное преобразование второго порядка было применено три раза к тому же эллиптическому полуленточному фильтру в порядке превратить его в полосовой фильтр. В каждом из этих трех случаев две различных функции прототипного фильтра были выбраны в порядке получить полосовой фильтр с полосой пропускания в пределах от 0,25 к 0,75. Положение функции DC не было важно, но было бы выгодно, если бы это было в середине между ребрами полосы пропускания в целевом фильтре. В первом случае выбранными функциями были левые и правые ребра полосы полосы пропускания фильтра lowpass во втором случае, они были левым ребром полосы и DC в третьем случае, они были DC и правильным ребром полосы.

Результат выбора различных функций

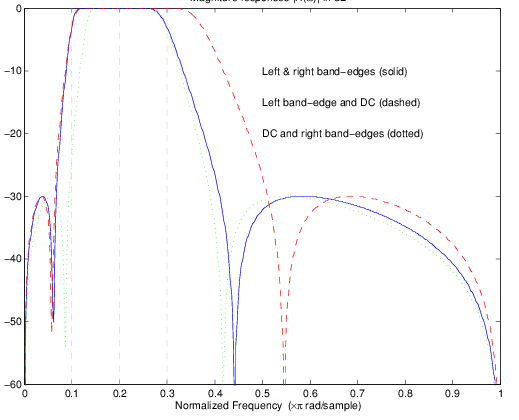
Результаты всех трех подходов полностью отличаются. Для каждого из них только выбранные функции были расположены точно, где они требовались. В первом случае DC перемещен к левому ребру полосы пропускания точно так же, как все другие функции близко к левому краю, сжимаемому туда. Во втором случае правильное ребро полосы пропускания было продвинутым выходом из ожидаемой цели, когда точное положение DC требовалось. В третьем случае левое ребро полосы пропускания вытянули к DC в порядке расположить его на правильной частоте. Заключение состоит в том, что, если только DC может быть где-нибудь в полосе пропускания, ребра полосы пропускания должны были быть выбраны для преобразования. Для большинства случаев, требующих расположения полос пропускания и полос задерживания, должны всегда выбирать разработчики, положение ребер прототипа просачиваются порядок убедиться, что они добираются, ребра цели просачиваются правильные места. Частотные характеристики для этих трех рассмотренных случаев показывают в фигуре. Прототипный фильтр был третьим порядком эллиптический фильтр lowpass с частотой среза в 0,5.

Код MATLAB^®, используемый, чтобы сгенерировать фигуру, дан здесь.

Прототипный фильтр является полуполосой, эллиптической, действительной, третий порядок lowpass фильтр:

[b, a] = ellip(3, 0.1, 30, 0.409);

В примере требования собираются создать действительный полосовой фильтр с ребрами полосы пропускания в 0,1 и 0.3 из действительного фильтра lowpass, имеющего частоту среза в 0,5. Это предпринято тремя различными способами. В первом подходе оба ребра полосы пропускания выбраны во втором подходе, левый край полосы пропускания и DC выбран, в то время как в третьем подходе DC и правый край полосы пропускания взяты:

[num1,den1] = iirlp2xn(b, a, [-0.5, 0.5], [0.1, 0.3]);
[num2,den2] = iirlp2xn(b, a, [-0.5, 0.0], [0.1, 0.2]);
[num3,den3] = iirlp2xn(b, a, [ 0.0, 0.5], [0.2, 0.3]);

Отображение от прототипного фильтра, чтобы предназначаться для фильтра

В целом отображение частоты преобразовывает прототипный фильтр, _Ho (z), к целевому фильтру, _HT (z), с помощью th-порядка _NA allpass фильтр, _HA (z). Общая форма allpass, сопоставляющего фильтр, дана в Обзоре Преобразований. Отображение частоты является математической операцией, которая заменяет каждый задерживатель прототипного фильтра с фильтром allpass. Существует два способа выполнить такое отображение. Выбор подхода зависит от того, как прототип и целевые фильтры представлены.

Когда прототипный фильтр th-порядка N дан с нулевой полюсом формой

$H_{o} (z) = \frac{\sum_{i = 1}^{N} (z - z_{i})}{\sum_{i = 1}^{N} (z - p_{i})}$

отображение заменит каждый полюс, _pi, и каждый нуль, _zi, со многими полюсами и нулями, равными порядку allpass, сопоставляющего фильтр:

$H_{o} (z) = \frac{\sum_{i = 1}^{N} (S \sum_{k = 0}^{N - 1} α_{k} z^{k} - z_{i} \cdot \sum_{k = 0}^{N - 1} α_{k} z^{N}^{- k})}{\sum_{i = 1}^{N} (S \sum_{k = 0}^{N - 1} α_{k} z^{k} - p_{i} \cdot \sum_{k = 0}^{N - 1} α_{k} z^{N}^{- k})}$

Корневое нахождение должно использоваться на выражениях в скобках в порядке найти полюса и нули целевого фильтра.

Когда прототипный фильтр описан в форме знаменателя числителя:

$H_{T} (z) = {\frac{β_{0} z^{N} + β_{1} z^{N - 1} + \dots + β_{N}}{α_{0} z^{N} + α_{1} z^{N - 1} + \dots + α_{N}} |}_{z = H_{A} (z)}$

Затем процесс отображения потребует многих сверток в порядке вычислить числитель и знаменатель целевого фильтра:

$H_{T} (z) = \frac{β_{1} N_{A} {(z)}^{N} + β_{2} N_{A} {(z)}^{N - 1} D_{A} (z) + \dots + β_{N} D_{A} {(z)}^{N}}{β_{1} N_{A} {(z)}^{N} + β_{2} N_{A} {(z)}^{N - 1} D_{A} (z) + \dots + β_{N} D_{A} {(z)}^{N}}$

Для каждого коэффициента _αi и _βi прототипного фильтра полиномы th-порядка _NA должны быть временами N, к которым применяют операцию свертки. Такой подход может вызвать погрешности округления для больших прототипных фильтров и/или фильтров отображения старшего разряда. В таком случае пользователь должен рассмотреть альтернативу для выполнения использования отображения через полюса и нули.

Сводные данные преобразований частоты

Преимущества

Большинство преобразований частоты описано решениями закрытой формы или может быть вычислено от набора линейных уравнений.
Они дают предсказуемые и знакомые результаты.
Высоты пульсации от прототипного фильтра сохраняются в целевом фильтре.
Они архитектурно призывают к переменным и адаптивным фильтрам.

Недостатки

Существуют случаи при использовании методов оптимизации, чтобы разработать необходимый фильтр, дает лучшие результаты.
Старшие преобразования увеличивают размерность целевого фильтра, который может дать дорогие конечные результаты.
Запуск с новых проектов помогает избежать заблокированный - в компромиссах.

Преобразования частоты для действительных фильтров

Обзор
Действительный сдвиг частоты
Действительный Lowpass к действительному Lowpass
Действительный Lowpass к действительному Highpass
Действительный Lowpass к действительной полосе пропускания
Действительный Lowpass к действительному Bandstop
Действительный Lowpass к многополосному действительному
Действительный Lowpass к многоточечному действительному

Обзор

В этом разделе рассматриваются действительные преобразования частоты, которые берут действительный прототип lowpass, фильтруют и преобразовывают его в различный действительный целевой фильтр. Целевому фильтру изменили его частотную характеристику относительно частотной характеристики прототипного фильтра согласно характеристике прикладного преобразования частоты.

Действительный сдвиг частоты

Действительное преобразование сдвига частоты использует allpass второго порядка, сопоставляющий фильтр. Это выполняет точное отображение одной выбранной функции частотной характеристики в ее новое местоположение, дополнительно перемещаясь и Найквиста и функции DC. Это эффективно перемещает целый ответ фильтра lowpass по расстоянию, заданному выбором функции от прототипного фильтра и целевого фильтра. Как действительное преобразование, это работает похожим способом к положительным и отрицательным частотам.

$H_{A} (z) = z^{- 1} \cdot \frac{1 - α z^{- 1}}{α - z^{- 1}}$

с α, данным

$α = {\begin{array}{l} \frac{потому что \frac{π}{2} (ω_{o l d} - 2 ω_{n e w})}{потому что \frac{π}{2} ω_{o l d}} & f o r & | потому что \frac{π}{2} (ω_{o l d} - 2 ω_{n e w}) | < 1 \\ \frac{\sin \frac{π}{2} (ω_{o l d} - 2 ω_{n e w})}{\sin \frac{π}{2} ω_{o l d}} & o t h e r w i s e \end{array}$

где

_ωold — Местоположение частоты выбранной функции в прототипном фильтре

_ωnew — Положение функции первоначально в _ωold в целевом фильтре

Следующий пример показывает, как это преобразование может использоваться, чтобы переместиться, ответ прототипа lowpass просачиваются любое направление. Обратите внимание на то, что, потому что целевой фильтр должен также быть действительным, ответ целевого фильтра будет по сути нарушен на частотах близко к Найквисту и близко к DC. Вот код MATLAB для генерации примера в фигуре.

Прототипный фильтр является полуполосой, эллиптической, действительной, третий порядок lowpass фильтр:

[b, a] = ellip(3, 0.1, 30, 0.409);

Преобразование в качестве примера перемещает функцию первоначально в 0,5 к 0,9:

[num,den] = iirshift(b, a, 0.5, 0.9);

Пример действительного отображения сдвига частоты

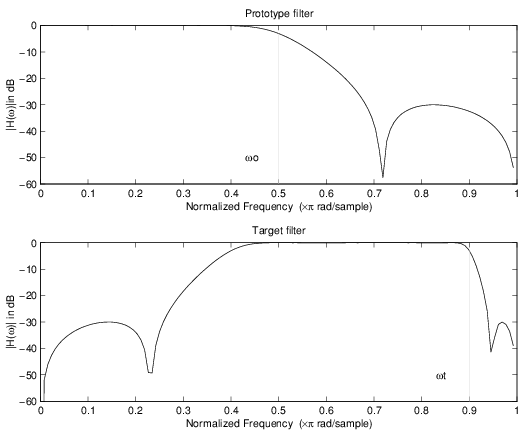
Действительный Lowpass к действительному Lowpass

Действительный фильтр lowpass к действительному преобразованию фильтра lowpass использует первый порядок allpass сопоставляющий фильтр. Это выполняет точное отображение одной функции частотной характеристики в новый DC хранения местоположения и зафиксированных функций Найквиста. Как действительное преобразование, это работает похожим способом к положительным и отрицательным частотам. Важно упомянуть, что использование отображения первого порядка гарантирует, что порядок фильтра после преобразования эквивалентен, это было первоначально.

$H_{A} (z) = - (\frac{1 - α z^{- 1}}{α - z^{- 1}})$

с α, данным

$α = \frac{\sin \frac{π}{2} (ω_{o l d} - ω_{n e w})}{\sin \frac{π}{2} (ω_{o l d} - ω_{n e w})}$

где

_ωold — Местоположение частоты выбранной функции в прототипном фильтре

_ωnew — Местоположение частоты той же функции в целевом фильтре

Пример ниже показов, как изменить частоту среза прототипного фильтра. Код MATLAB для этого примера показывают в следующей фигуре.

Прототипный фильтр является полуполосой, эллиптической, действительной, фильтр третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

Частота среза перемещается от 0,5 до 0,75:

[num,den] = iirlp2lp(b, a, 0.5, 0.75);

Пример действительного Lowpass к действительному отображению Lowpass

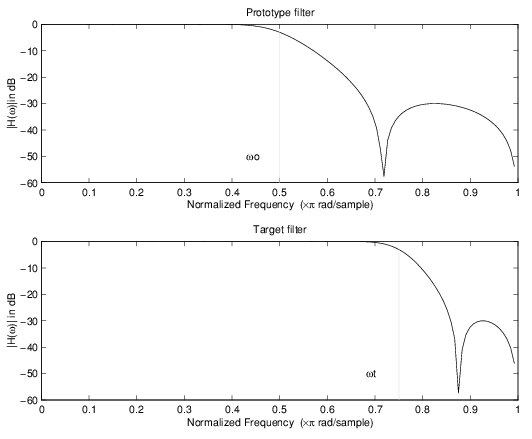
Действительный Lowpass к действительному Highpass

Действительный фильтр lowpass к действительному преобразованию фильтра highpass использует первый порядок allpass сопоставляющий фильтр. Это выполняет точное отображение одной функции частотной характеристики в новое местоположение, дополнительно подкачивающее функции Найквиста и DC. Как действительное преобразование, это работает похожим способом к положительным и отрицательным частотам. Точно так же, как в предыдущем преобразовании из-за использования отображения первого порядка, порядок фильтра до и после преобразования является тем же самым.

$H_{A} (z) = - (\frac{1 + α z^{- 1}}{α + z^{- 1}})$

с α, данным

$α = - (\frac{потому что \frac{π}{2} (ω_{o l d} + ω_{n e w})}{потому что \frac{π}{2} (ω_{o l d} - ω_{n e w})})$

где

_ωold — Местоположение частоты выбранной функции в прототипном фильтре

_ωnew — Местоположение частоты той же функции в целевом фильтре

Пример ниже показов, как преобразовать фильтр lowpass в highpass, фильтрует с произвольно выбранной частотой среза. В коде MATLAB ниже, фильтр lowpass преобразован в highpass с частотой среза, переключенной от 0,5 до 0,75. Результаты показывают в фигуре.

Прототипный фильтр является полуполосой, эллиптической, действительной, фильтр третьего порядка:

[b, a] = ellip(3, 0.1, 30, 0.409);

Пример перемещает частоту среза от 0,5 до 0,75:

[num,den] = iirlp2hp(b, a, 0.5, 0.75);

Пример действительного Lowpass к действительному отображению Highpass

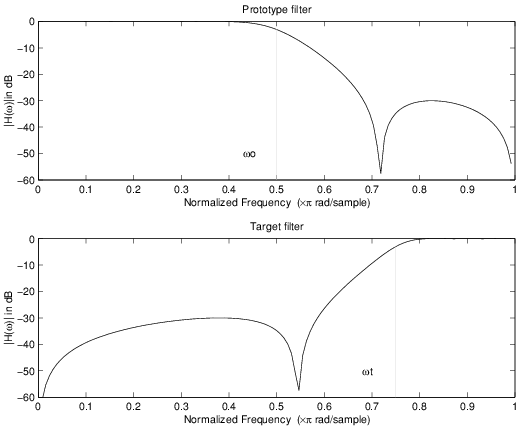
Действительный Lowpass к действительной полосе пропускания

Действительный фильтр lowpass к действительному преобразованию полосового фильтра использует allpass второго порядка, сопоставляющий фильтр. Это выполняет точное отображение двух функций частотной характеристики в их новое местоположение, дополнительно перемещающее функцию DC и сохраняющее зафиксированную функцию Найквиста. Как действительное преобразование, это работает похожим способом к положительным и отрицательным частотам.

$H_{A} (z) = - (\frac{1 - β (1 + α) z^{- 1} - α z^{- 2}}{α - β (1 + α) z^{- 1} + z^{- 2}})$

с α и β, данным

$α = \frac{\sin \frac{π}{4} (2 ω_{o l d} - ω_{n e w, 2} + ω_{n e w, 1})}{\sin \frac{π}{4} (2 ω_{o l d} + ω_{n e w, 2} - ω_{n e w, 1})}$

$β = потому что \frac{π}{2} (ω_{n e w, 1} + ω_{n e w, 2})$

где

_ωold — Местоположение частоты выбранной функции в прототипном фильтре

_ωnew,1 — Положение функции первоначально в _(-ωold) в целевом фильтре

_ωnew,2 — Положение функции первоначально в _(+ωold) в целевом фильтре

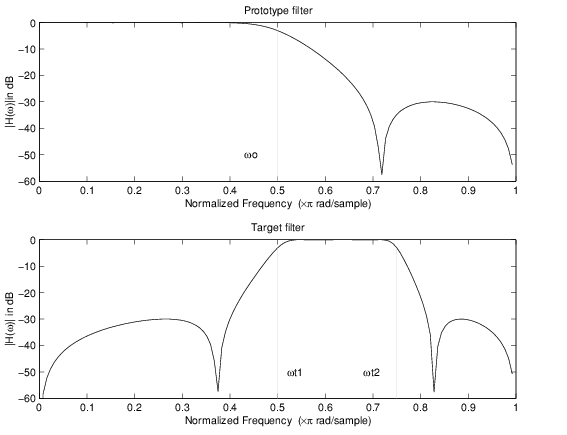
Пример ниже показов, как переместить ответ прототипа lowpass, просачивается любое направление. Обратите внимание на то, что, потому что целевой фильтр должен также быть действительным, ответ целевого фильтра будет по сути нарушен на частотах близко к Найквисту и близко к DC. Вот код MATLAB для генерации примера в фигуре.

Прототипный фильтр является полуполосой, эллиптической, действительной, третий порядок lowpass фильтр:

[b, a] = ellip(3, 0.1, 30, 0.409);

Преобразование в качестве примера создает полосу пропускания между 0,5 и 0.75:

[num,den] = iirlp2bp(b, a, 0.5, [0.5, 0.75]);

Пример действительного Lowpass к действительному полосовому отображению

Действительный Lowpass к действительному Bandstop

Действительный фильтр lowpass к действительному преобразованию заграждающего фильтра использует allpass второго порядка, сопоставляющий фильтр. Это выполняет точное отображение двух функций частотной характеристики в их новое местоположение, дополнительно перемещающее функцию Найквиста и сохраняющее зафиксированную функцию DC. Это эффективно создает полосу задерживания между выбранными местоположениями частоты в целевом фильтре. Как действительное преобразование, это работает похожим способом к положительным и отрицательным частотам.

$H_{A} (z) = \frac{1 - β (1 + α) z^{- 1} + α z^{- 2}}{α - β (1 + α) z^{- 1} + z^{- 2}}$

с α и β, данным

$\begin{array}{l} α = \frac{потому что \frac{π}{4} (2 ω_{o l d} + ω_{n e w, 2} - ω_{n e w, 1})}{потому что \frac{π}{4} (2 ω_{o l d} - ω_{n e w, 2} + ω_{n e w, 1})} \\ β = потому что \frac{π}{2} (ω_{n e w, 1} + ω_{n e w, 2}) \end{array}$

где

_ωold — Местоположение частоты выбранной функции в прототипном фильтре

_ωnew,1 — Положение функции первоначально в _(-ωold) в целевом фильтре

_ωnew,2 — Положение функции первоначально в _(+ωold) в целевом фильтре

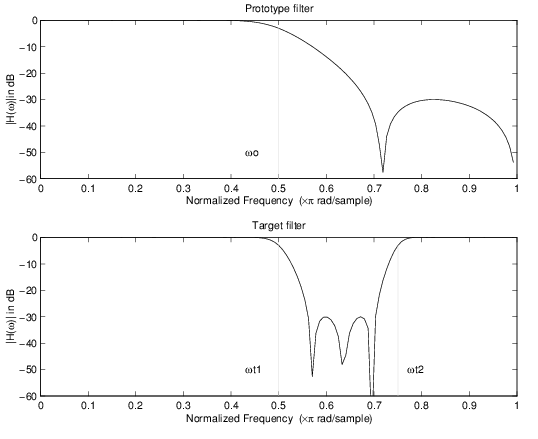
Следующий пример показывает, как это преобразование может использоваться, чтобы преобразовать прототип lowpass фильтр с частотой среза в 0,5 в действительный заграждающий фильтр с той же полосой пропускания и структурой пульсации полосы задерживания и полосой задерживания, расположенной между 0,5 и 0.75. Вот код MATLAB для генерации примера в фигуре.

Прототипный фильтр является полуполосой, эллиптической, действительной, третий порядок lowpass фильтр:

[b, a] = ellip(3, 0.1, 30, 0.409);

Преобразование в качестве примера создает полосу задерживания от 0,5 до 0,75:

[num,den] = iirlp2bs(b, a, 0.5, [0.5, 0.75]);

Пример действительного Lowpass к действительному отображению Bandstop

Действительный Lowpass к многополосному действительному

Это старшее преобразование выполняет точное отображение одной выбранной функции прототипной частотной характеристики фильтра во многие новые местоположения в целевом фильтре. Его наиболее популярный способ использования должен преобразовать действительный lowpass с предопределенной полосой пропускания и пульсациями полосы задерживания в действительный многополосный фильтр с N произвольные ребра полосы, где N является порядком allpass, сопоставляющего фильтр.

$\begin{array}{l} H_{A} (z) = S \frac{\sum_{i = 0}^{N} α_{i}^{} z^{- i}}{\sum_{i = 0}^{N} α_{i}^{} z^{- N + i}} \\ α_{0} = 1 \end{array}$

Коэффициентами α дают

${\begin{cases} \begin{matrix} α_{0} = 1 & k = 1, \dots, N \end{matrix} \\ α_{k} = - S \frac{\sin \frac{π}{2} (N ω_{n e w} + {(- 1)}^{k} ω_{o l d})}{\sin \frac{π}{2} ((N - 2 k) ω_{n e w} + {(- 1)}^{k} ω_{o l d})} \end{cases}$

где

_ωold,k — Местоположение частоты первой функции в прототипном фильтре

_ωnew,k — Положение функции первоначально в _ωold,k в целевом фильтре

Фактор мобильности, S, задает мобильность или или DC или функция Найквиста:

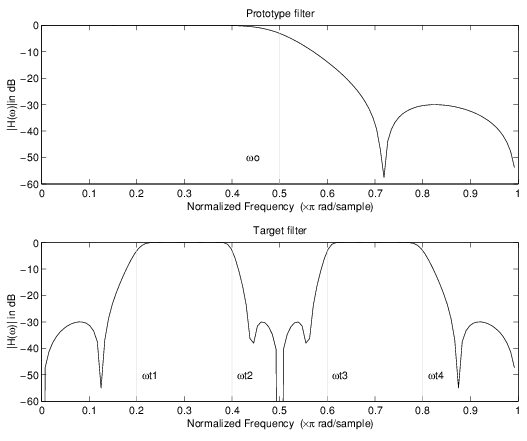
$S = {\begin{matrix} 1 & N y q u i s t \\ - 1 & D C \end{matrix}$

Пример ниже показов, как это преобразование может использоваться, чтобы преобразовать прототип lowpass фильтр с частотой среза в 0,5 в фильтр, располагающий много полос на произвольных частотах ребра 1/5, 2/5, 3/5 и 4/5. S параметра был таков, что существует полоса пропускания в DC. Вот код MATLAB для генерации фигуры.

Прототипный фильтр является полуполосой, эллиптической, действительной, третий порядок lowpass фильтр:

[b, a] = ellip(3, 0.1, 30, 0.409);

Преобразование в качестве примера создает три полосы задерживания, от DC до 0,2, от 0,4 до 0,6 и от 0,8 до Найквиста:

[num,den] = iirlp2mb(b, a, 0.5, [0.2, 0.4, 0.6, 0.8], `pass');

Пример действительного Lowpass к действительному многополосному отображению

Действительный Lowpass к многоточечному действительному

Это старшее преобразование частоты выполняет точное отображение многих выбранных функций прототипной частотной характеристики фильтра на их новые местоположения в целевом фильтре. Фильтр отображения дан общей БИХ-формой полинома передаточной функции, как приведено ниже.

$\begin{array}{l} H_{A} (z) = S \frac{\sum_{i = 0}^{N} α_{i} z^{- i}}{\sum_{i = 0}^{N} α_{i} z^{- N + i}} \\ α_{0} = 1 \end{array}$

Для th-порядка N многоточечное преобразование частоты коэффициенты α

${\begin{array}{l} \sum_{i = 1}^{N} α_{N - i} z_{o l d, k} \cdot z_{n e w, k}^{i} - S \cdot z_{n e w, k}^{N - i} = - z_{o l d, k} - S \cdot z_{n e w, k} \\ z_{o l d, k} = e^{j π ω_{o l d, k}} \\ z_{n e w, k} = e^{j π ω_{n e w, k}} \\ k = 1, \dots, N \end{array}$

где

_ωold,k — Местоположение частоты первой функции в прототипном фильтре

_ωnew,k — Положение функции первоначально в _ωold,k в целевом фильтре

Фактор мобильности, S, задает мобильность или DC или функции Найквиста:

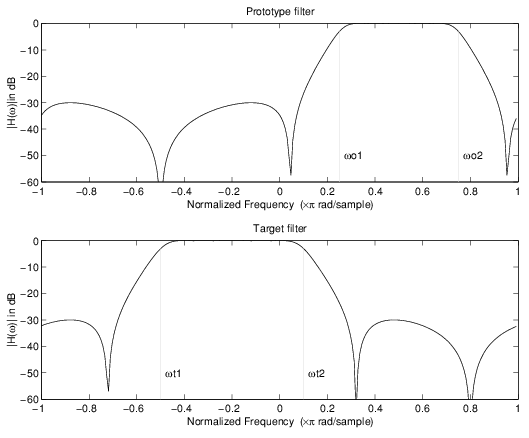
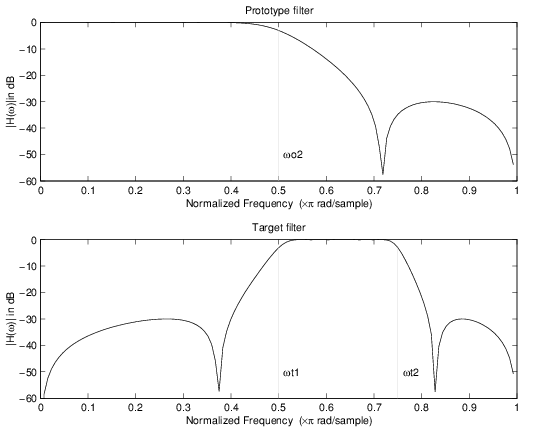
$S = {\begin{matrix} 1 & N y q u i s t \\ - 1 & D C \end{matrix}$

Пример ниже показов, как это преобразование может использоваться, чтобы переместить функции прототипа lowpass фильтр первоначально в-0.5 и 0.5 к их новым местоположениям в 0,5 и 0.75, эффективно меняя положение полосы пропускания фильтра. Вот код MATLAB для генерации фигуры.

Прототипный фильтр является полуполосой, эллиптической, действительной, третий порядок lowpass фильтр:

[b, a] = ellip(3, 0.1, 30, 0.409);

Преобразование в качестве примера создает полосу пропускания от 0,5 до 0,75:

[num,den] = iirlp2xn(b, a, [-0.5, 0.5], [0.5, 0.75], `pass');

Пример действительного Lowpass к действительному многоточечному отображению

Преобразования частоты для комплексных фильтров

Обзор
Комплексный сдвиг частоты
Действительный Lowpass, чтобы объединить полосу пропускания
Действительный Lowpass, чтобы объединить Bandstop
Действительный Lowpass, чтобы объединить многополосный
Действительный Lowpass, чтобы объединить многоточечный
Объедините полосу пропускания, чтобы объединить полосу пропускания

Обзор

В этом разделе рассматриваются комплексное преобразование частоты, которые берут комплексный прототипный фильтр и преобразовывают его в различный комплексный целевой фильтр. Целевому фильтру изменили его частотную характеристику относительно частотной характеристики прототипного фильтра согласно характеристике прикладного преобразования частоты от:

Комплексный сдвиг частоты

Комплексное преобразование сдвига частоты является самым простым преобразованием первого порядка, которое выполняет точное отображение одной выбранной функции частотной характеристики в ее новое местоположение. В то же время это вращает целый ответ прототипа lowpass фильтр по расстоянию, заданному выбором функции от прототипного фильтра и целевого фильтра.

$H_{A} (z) = α z^{- 1}$

с α, данным

$α = e^{j 2 π (ν_{n e w} - ν_{o l d})}$

где

_ωold — Местоположение частоты выбранной функции в прототипном фильтре

_ωnew — Положение функции первоначально в _ωold в целевом фильтре

Особый случай комплексного сдвига частоты является a, так называемым, Гильбертовым Преобразователем. Это может быть разработано путем установки параметра на |α | = 1, который является

$α = {\begin{matrix} 1 & f o r w a r d \\ - 1 & i n v e r s e \end{matrix}$

Пример ниже показов, как применить это преобразование, чтобы вращать ответ прототипа lowpass, просачивается любое направление. Обратите внимание на то, что, потому что преобразование может быть достигнуто простым оператором сдвига фазы, все функции прототипного фильтра будут перемещены той же суммой. Вот код MATLAB для генерации примера в фигуре.

Прототипный фильтр является полуполосой, эллиптической, действительной, третий порядок lowpass фильтр:

[b, a] = ellip(3, 0.1, 30, 0.409);

Преобразование в качестве примера перемещает функцию первоначально в 0,5 к 0,3:

[num,den] = iirshiftc(b, a, 0.5, 0.3);

Пример комплексного отображения сдвига частоты

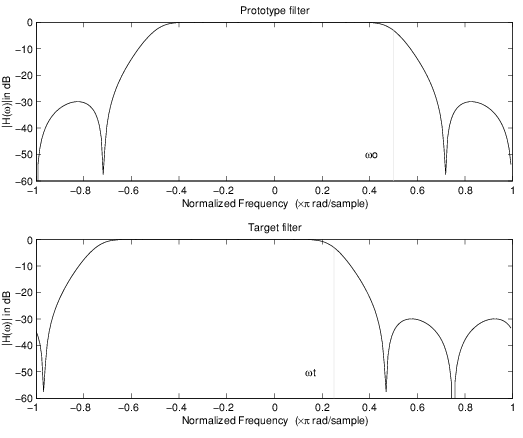
Действительный Lowpass, чтобы объединить полосу пропускания

Это преобразование первого порядка выполняет точное отображение одной выбранной функции прототипной частотной характеристики фильтра в два новых места в целевом фильтре, создающем полосу пропускания между ними. И Найквист и функции DC могут быть перемещены с остальной частью частотной характеристики.

$H_{A} (z) = \frac{β - α z^{- 1}}{z^{- 1} - α β}$

with α и β дают

$\begin{array}{l} α = \frac{\sin \frac{π}{4} (2 ω_{o l d} - ω_{n e w, 2} + ω_{n e w, 1})}{\sin π (2 ω_{o l d} + ω_{n e w, 2} - ω_{n e w, 1})} \\ β = e^{- j π (ω_{n e w} - ω_{o l d})} \end{array}$

где

_ωold — Местоположение частоты выбранной функции в прототипном фильтре

_ωnew,1 — Положение функции первоначально в _(-ωold) в целевом фильтре

_ωnew,2 — Положение функции первоначально в _(+ωold) в целевом фильтре

Следующий пример показывает использование такого преобразования для преобразования действительной полуполосы lowpass фильтр в комплексный полосовой фильтр с ребрами полосы в 0,5 и 0.75. Вот код MATLAB для генерации примера в фигуре.

Прототипный фильтр является половиной полосы, эллиптической, действительной, третий порядок lowpass фильтр:

[b, a] = ellip(3, 0.1, 30, 0.409);

Преобразование создает полосу пропускания от 0,5 до 0,75:

[num,den] = iirlp2bpc(b, a, 0.5, [0.5 0.75]);

Пример действительного Lowpass, чтобы объединить полосовое отображение

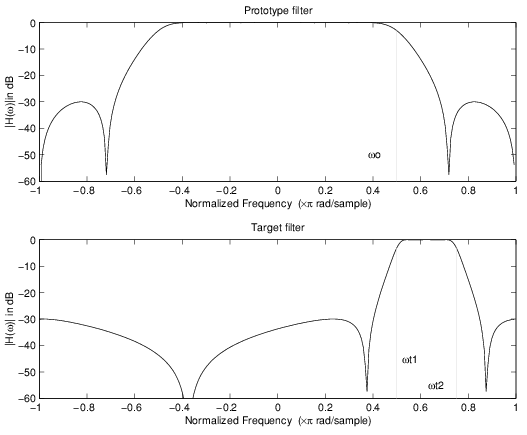
Действительный Lowpass, чтобы объединить Bandstop

Это преобразование первого порядка выполняет точное отображение одной выбранной функции прототипной частотной характеристики фильтра в два новых места в целевом фильтре, создающем полосу задерживания между ними. И Найквист и функции DC могут быть перемещены с остальной частью частотной характеристики.

$H_{A} (z) = \frac{β - α z^{- 1}}{α β - z^{- 1}}$

с α и β дают

$\begin{array}{l} α = \frac{потому что π (2 ω_{o l d} + ν_{n e w, 2} - ν_{n e w, 1})}{потому что π (2 ω_{o l d} - ν_{n e w, 2} + ν_{n e w, 1})} \\ β = e^{- j π (ω_{n e w} - ω_{o l d})} \end{array}$

где

_ωold — Местоположение частоты выбранной функции в прототипном фильтре

_ωnew,1 — Положение функции первоначально в _(-ωold) в целевом фильтре

_ωnew,2 — Положение функции первоначально в _(+ωold) в целевом фильтре

Пример ниже показов использование такого преобразования для преобразования действительной полуполосы lowpass фильтрует в комплексный заграждающий фильтр с ребрами полосы в 0,5 и 0.75. Вот код MATLAB для генерации примера в фигуре.

Прототипный фильтр является полуполосой, эллиптической, действительной, третий порядок lowpass фильтр:

[b, a] = ellip(3, 0.1, 30, 0.409);

Преобразование создает полосу задерживания от 0,5 до 0,75:

[num,den] = iirlp2bsc(b, a, 0.5, [0.5 0.75]);

Пример действительного Lowpass, чтобы объединить отображение Bandstop

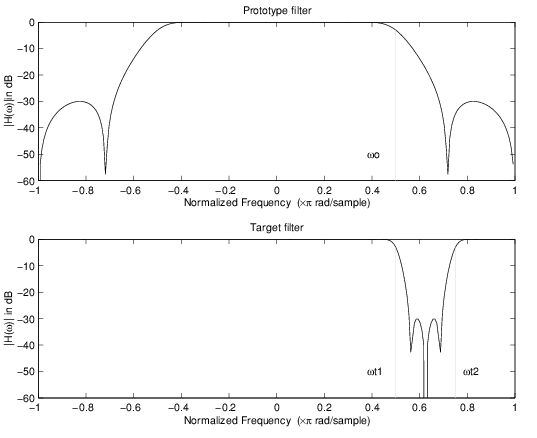
Действительный Lowpass, чтобы объединить многополосный

Это старшее преобразование выполняет точное отображение одной выбранной функции прототипной частотной характеристики фильтра во многие новые местоположения в целевом фильтре. Его наиболее популярный способ использования должен преобразовать действительный lowpass с предопределенной полосой пропускания и пульсациями полосы задерживания в многополосный фильтр с произвольными ребрами полосы. Порядок фильтра отображения должен быть даже, который соответствует четному числу ребер полосы в целевом фильтре. allpass комплекса th-порядка N, сопоставляющий фильтр, дан следующей общей формой передаточной функции:

$\begin{array}{l} H_{A} (z) = S \frac{\sum_{i = 0}^{N} α_{i} z^{- i}}{\sum_{i = 0}^{N} α_{i} \pm z^{- N + i}} \\ α_{0} = 1 \end{array}$

Коэффициенты α вычисляются от системы линейных уравнений:

${\begin{cases} \sum_{i = 1}^{N} ℜ (α_{i}) \cdot [потому что β_{1, k} - потому что β_{2, k}] + ℑ (α_{i}) \cdot [\sin β_{1, k} + \sin β_{2, k}] = потому что β_{3, k} \\ \sum_{i = 1}^{N} ℜ (α_{i}) \cdot [\sin β_{1, k} - \sin β_{2, k}] - ℑ (α_{i}) \cdot [потому что β_{1, k} + потому что β_{2, k}] = \sin β_{3, k} \\ β_{1, k} = - π [ν_{o l d} \cdot {(- 1)}^{k} + ν_{n e w, k} (N - k)] \\ β_{2, k} = - π [Δ C + ν_{n e w, k} k] \\ β_{3, k} = - π [ν_{o l d} \cdot {(- 1)}^{k} + ν_{n e w, k} N] \\ k = 1 \dots N \end{cases}$

где

_ωold — Местоположение частоты выбранной функции в прототипном фильтре

_ωnew,i — Положение функций первоначально в ±_ωold в целевом фильтре

Параметр S является дополнительным фактором вращения расстоянием частоты ΔC, давая дополнительную гибкость достижения необходимого отображения:

$S = e^{- j π Δ C}$

Пример показывает использование такого преобразования для преобразования прототипа действительный фильтр lowpass с частотой среза в 0,5 в многополосный комплексный фильтр с ребрами полосы в 0,2, 0.4, 0.6 и 0.8, создавая две полосы пропускания вокруг модульного круга. Вот код MATLAB для генерации фигуры.

Пример действительного Lowpass, чтобы объединить многополосное отображение

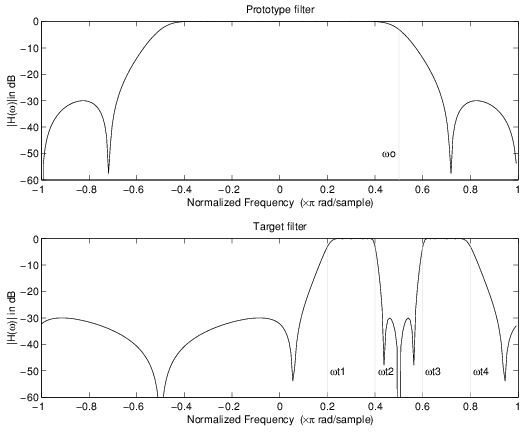
Прототипный фильтр является полуполосой, эллиптической, действительной, третий порядок lowpass фильтр:

[b, a] = ellip(3, 0.1, 30, 0.409);

Преобразование в качестве примера создает две комплексных полосы пропускания:

[num,den] = iirlp2mbc(b, a, 0.5, [0.2, 0.4, 0.6, 0.8]);

Действительный Lowpass, чтобы объединить многоточечный

Это старшее преобразование выполняет точное отображение многих выбранных функций прототипной частотной характеристики фильтра на их новые местоположения в целевом фильтре. allpass комплекса th-порядка N, сопоставляющий фильтр, дан следующей общей формой передаточной функции.

$\begin{array}{l} H_{A} (z) = S \frac{\sum_{i = 0}^{N} α_{i} z^{- i}}{\sum_{i = 0}^{N} α_{i} \pm z^{- N + i}} \\ α_{0} = 1 \end{array}$

Коэффициенты α могут быть вычислены от системы линейных уравнений:

${\begin{cases} \sum_{i = 1}^{N} ℜ (α_{i}) \cdot [потому что β_{1, k} - потому что β_{2, k}] + ℑ (α_{i}) \cdot [\sin β_{1, k} + \sin β_{2, k}] = потому что β_{3, k} \\ \sum_{i = 1}^{N} ℜ (α_{i}) \cdot [\sin β_{1, k} - \sin β_{2, k}] - ℑ (α_{i}) \cdot [потому что β_{1, k} + потому что β_{2, k}] = \sin β_{3, k} \\ β_{1, k} = - \frac{π}{2} [ω_{o l d, k} + ω_{n e w, k} (N - k)] \\ β_{2, k} = - \frac{π}{2} [2 Δ C + ω_{n e w, k} k] \\ β_{3, k} = - \frac{π}{2} [ω_{o l d, k} + ω_{n e w, k} N] \\ k = 1 \dots N \end{cases}$

где

_ωold,k — Местоположение частоты первой функции в прототипном фильтре

_ωnew,k — Положение функции первоначально в _ωold,k в целевом фильтре

$S = e^{- j π Δ C}$

Следующий пример показывает, как это преобразование может использоваться, чтобы переместиться, тот выбрал функцию прототипа lowpass фильтр первоначально в-0.5 к двум новым частотам-0.5 и 0.1 и вторую функцию прототипного фильтра от 0,5 до новых местоположений в-0.25 и 0.3. Это создает две несимметричных полосы пропускания вокруг модульного круга, создавая комплексный фильтр. Вот код MATLAB для генерации фигуры.

Прототипный фильтр является полуполосой, эллиптической, действительной, третий порядок lowpass фильтр:

[b, a] = ellip(3, 0.1, 30, 0.409);

Преобразование в качестве примера создает две несимметричных полосы пропускания:

[num,den] = iirlp2xc(b,a,0.5*[-1,1,-1,1], [-0.5,-0.25,0.1,0.3]);

Пример действительного Lowpass, чтобы объединить многоточечное отображение

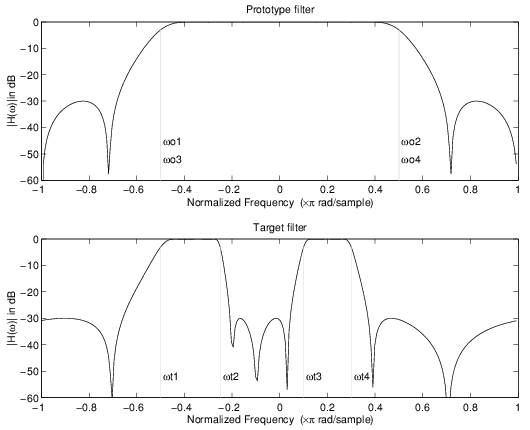
Объедините полосу пропускания, чтобы объединить полосу пропускания

Это преобразование первого порядка выполняет точное отображение двух выбранных функций прототипной частотной характеристики фильтра в два новых места в целевом фильтре. Его наиболее популярный способ использования должен настроить ребра комплексного полосового фильтра.

$H_{A} (z) = \frac{α (γ - β z^{- 1})}{z^{- 1} - β γ}$

с α и β дают

$\begin{array}{l} α = \frac{\sin \frac{π}{4} ((ω_{o l d, 2} - ω_{o l d, 1}) - (ω_{n e w, 2} - ω_{n e w, 1}))}{\sin \frac{π}{4} ((ω_{o l d, 2} - ω_{o l d, 1}) + (ω_{n e w, 2} - ω_{n e w, 1}))} \\ α = e^{- j π (ω_{o l d, 2} - ω_{o l d, 1})} \\ γ = e^{- j π (ω_{n e w, 2} - ω_{n e w, 1})} \end{array}$

где

_ωold,1 — Местоположение частоты первой функции в прототипном фильтре

_ωold,2 — Местоположение частоты второй функции в прототипном фильтре

_ωnew,1 — Положение функции первоначально в _ωold,1 в целевом фильтре

_ωnew,2 — Положение функции первоначально в _ωold,2 в целевом фильтре

Следующий пример показывает, как это преобразование может использоваться, чтобы изменить положение полосы пропускания прототипного фильтра, или действительного или комплексного. В примере ниже прототипа фильтруют полосу пропускания, заполненную от 0,5 до 0,75. Это было преобразовано в наличие полосы пропускания между-0.5 и 0.1. Вот код MATLAB для генерации фигуры.

Прототипный фильтр является полуполосой, эллиптической, действительной, третий порядок lowpass фильтр:

[b, a] = ellip(3, 0.1, 30, 0.409);

Преобразование в качестве примера создает полосу пропускания от 0,25 до 0,75:

[num,den] = iirbpc2bpc(b, a, [0.25, 0.75], [-0.5, 0.1]);

Пример комплексной полосы пропускания, чтобы объединить полосовое отображение

Документация