В последние годы число и разнообразие применений нечеткой логики значительно увеличилось. Приложения колеблются от потребительских товаров, таких как камеры, видеокамеры, стиральные машины и микроволновые печи к управлению производственным процессом, медицинскому инструментированию, системам поддержки принятия решений и выбору портфеля.
Чтобы понять рост интереса к нечеткой логике, необходимо сначала определиться, что же такое нечеткая логика.
Нечеткая логика имеет два различных значения. В узком смысле нечеткая логика является логической системой, которая является расширением многозначной логики. Однако в более широком смысле нечеткая логика (FL) почти синонимична с теорией нечетких множеств, теорией, которая относится к классам объектов с нерезкими контурами, в которых членство является вопросом степени. В этой перспективе нечеткая логика в ее узком смысле является ответвлением FL. Даже в ее более узком определении, нечеткая логика отличается и по концепции и по веществу от традиционных многозначных логических систем.
В программном обеспечении Fuzzy Logic Toolbox™ нечеткая логика должна быть интерпретирована как FL, то есть, нечеткая логика в ее широком смысле. Основные идеи, лежащие в основе FL, объяснены в Основах Нечеткой логики. То, что может быть добавлено, - то, что фундаментальное понятие, лежащее в основе FL, является фундаментальным понятием лингвистической переменной, то есть, переменная, значения которой являются словами, а не числами. В действительности большая часть FL может быть просмотрена как методология для вычисления со словами, а не числами. Несмотря на то, что слова по сути менее точны, чем числа, их использование ближе к человеческой интуиции. Кроме того, вычисление со словами использует допуск к неточности и таким образом понижает стоимость решения.
Другое фундаментальное понятие в FL, который играет центральную роль в большинстве ее приложений, является фундаментальным понятием нечеткого если затем правило или, просто, нечеткое правило. Несмотря на то, что основанные на правилах системы имеют долгую историю использования в Искусственном интеллекте (AI), что отсутствует в таких системах, механизм для контакта с нечеткими следствиями и нечеткими антецедентами. В нечеткой логике этот механизм обеспечивается исчислением нечетких правил. Исчисление нечетких правил служит основанием для того, что может быть названо Нечеткой Зависимостью и Командным языком (FDCL). Несмотря на то, что FDCL не используется явным образом в тулбоксе, это - эффективно одна из своих основных составляющих. В большинстве приложений нечеткой логики решение для нечеткой логики является, в действительности, переводом человеческого решения в FDCL.
Тренд, который растет в видимости, относится к использованию нечеткой логики в сочетании с нейрокомпьютингом и генетическими алгоритмами. В более общем плане нечеткая логика, нейрокомпьютинг и генетические алгоритмы могут быть просмотрены как основные составляющие того, что может быть названо мягким вычислением. В отличие от традиционного, трудного вычисления, мягкое вычисление размещает неточность реального мира. Руководящий принцип мягкого вычисления: Используйте допуск к неточности, неуверенности и частичной истине, чтобы достигнуть tractability, робастности и низкой стоимости решения. В будущем, мягком вычислении мог играть все больше важная роль в концепции и проекте систем, MIQ которых (Машина IQ) намного выше, чем та из систем, разработанных условными методами.
Среди различных комбинаций методологий в мягком вычислении то, которое имеет самую высокую видимость в данный момент, является тем нечеткой логики и нейрокомпьютинга, ведя к нейронечетким системам. В нечеткой логике такие системы играют особенно важная роль в индукции правил от наблюдений. Эффективный метод, разработанный доктором Роджером Дженгом с этой целью, называется ANFIS (Адаптивная Нейронечеткая Система Вывода). Этот метод является важным компонентом тулбокса.
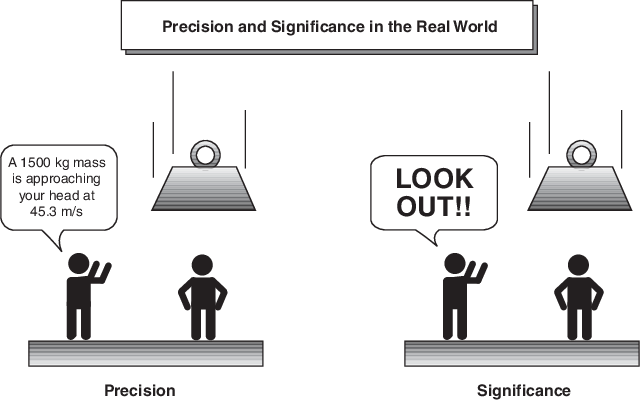
Нечеткая логика - все об относительной важности точности: Как важный должно быть точно правильно, когда грубый ответ сделает?
Можно использовать программное обеспечение Fuzzy Logic Toolbox с MATLAB® техническое вычислительное программное обеспечение как инструмент для решения проблем с нечеткой логикой. Нечеткая логика является захватывающей областью исследования, потому что это делает хорошее задание обменивания между значением и точностью — что-то, что люди были управлением в течение очень долгого времени.
В этом смысле нечеткая логика является и старой и новой, потому что, несмотря на то, что современная и методическая наука о нечеткой логике все еще молода, концепции нечеткой логики полагаются на старые навыки человеческого мышления.
Нечеткая логика является удобным способом сопоставить входной пробел с выходным пробелом. Вход Mapping, чтобы вывести является отправной точкой для всего. Рассмотрите следующие примеры:
С информацией о том, насколько хороший ваш сервис был в ресторане, система нечеткой логики может сказать вам, каков совет должен быть.
С вашей спецификацией того, как горячий вы хотите воду, система нечеткой логики может настроить клапан крана к правильной установке.
С информацией о том, как далеко далеко предмет вашей фотографии, система нечеткой логики может фокусировать линзу для вас.
С информацией о том, как быстро автомобиль идет и как трудно двигатель работает, система нечеткой логики может переключить скорости для вас.
Графический пример карты ввода - вывода показывают в следующей фигуре.
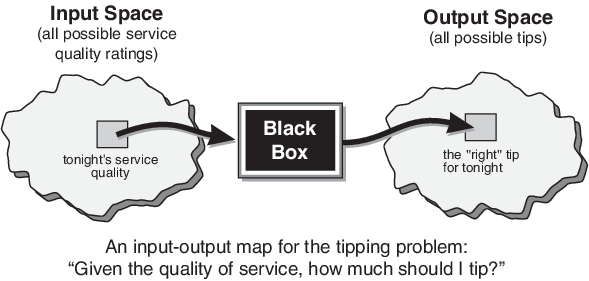
Определение ассигновать сумма в размере совета требует входных параметров отображения к соответствующим выходным параметрам. Между входом и выводом, предыдущие данные показывают черный квадрат, который может содержать любое количество вещей: нечеткие системы, линейные системы, экспертные системы, нейронные сети, дифференциальные уравнения, интерполировали многомерные интерполяционные таблицы, или даже духовного советника, только чтобы назвать несколько возможных вариантов. Очевидно список мог продолжиться и на.
Из десятков способов заставить черный квадрат работать, оказывается, что нечеткий часто самый лучший путь. Почему это должно быть? Как Lotfi Zadeh, кто считается родительским элементом нечеткой логики, когда-то отметил: "Почти в каждом случае можно создать тот же продукт без нечеткой логики, но нечеткий является быстрее и более дешевым".
Вот список общих наблюдений о нечеткой логике:
Нечеткую логику концептуально легко понять.
Математические понятия позади нечеткого обоснования очень просты. Нечеткая логика является более интуитивным подходом без далеко идущей сложности.
Нечеткая логика гибка.
С любой данной системой это легко к слою на большей функциональности, не начиная снова с нуля.
Нечеткая логика терпима к неточным данным.
Все неточно, если вы смотрите достаточно тесно, но больше, чем это, большинство вещей неточно даже на тщательном контроле. Нечеткое обоснование встраивает это понимание в процесс вместо того, чтобы прикрепить его на конец.
Нечеткая логика может смоделировать нелинейные функции произвольной сложности.
Можно создать нечеткую систему, чтобы совпадать с любым набором данных ввода - вывода. Этот процесс сделан особенно легким адаптивными методами как Адаптивные нейронечеткие системы вывода (ANFIS), которые доступны в программном обеспечении Fuzzy Logic Toolbox.
Нечеткая логика может быть создана сверх опыта экспертов.
На прямом контрасте по отношению к нейронным сетям, которые берут данные тренировки и генерируют непрозрачные, непроницаемые модели, нечеткая логика позволяет вам полагаться на опыт людей, которые уже понимают вашу систему.
Нечеткая логика может быть смешана с обычными методами управления.
Нечеткие системы не обязательно заменяют обычные методы управления. Во многих случаях нечеткие системы увеличивают их и упрощают их реализацию.
Нечеткая логика основана на естественном языке.
Основанием для нечеткой логики является основание для человеческого общения. Это наблюдение подкрепляет многие из других операторов о нечеткой логике. Поскольку нечеткая логика основана на структурах качественного описания, используемого на обыденном языке, нечеткая логика проста в использовании.
Последний оператор является, возможно, самым важным и заслуживает большего количества обсуждения. Естественный язык, который используется простыми людьми ежедневно, был сформирован на тысячи лет истории человечества, чтобы быть удобным и эффективным. Предложения, написанные в обычном языке, представляют триумф эффективной коммуникации.
Нечеткая логика не является панацеей. Когда вы не должны использовать нечеткую логику? Самый безопасный оператор является первым, сделанным в этом введении: нечеткая логика является удобным способом сопоставить входной пробел с выходным пробелом. Если вы находите, что это не удобно, попробуйте что-то еще. Если простое решение уже существует, используйте его. Нечеткая логика является кодированием здравого смысла — используют здравый смысл, когда вы реализуете его, и вы, вероятно, примете правильное решение. Многие контроллеры, например, делают прекрасное задание, не используя нечеткую логику. Однако, если вы будете не торопиться, чтобы познакомиться с нечеткой логикой, вы будете видеть, что это может быть очень мощный инструмент для контакта быстро и эффективно с неточностью и нелинейностью.
Можно создать и отредактировать нечеткие системы вывода с программным обеспечением Fuzzy Logic Toolbox. Можно создать эти системы с помощью графических инструментов или функций командной строки, или можно сгенерировать их автоматически использующий или кластеризирующийся или адаптивные нейронечеткие методы.
Если у вас есть доступ к программному обеспечению Simulink®, можно легко протестировать нечеткую систему в среде симуляции блок-схемы.
Тулбокс также позволяет вам запустить свои собственные автономные программы C непосредственно. Это сделано возможным автономным Нечетким Механизмом логического вывода, который читает нечеткие системы, сохраненные из сеанса работы с MATLAB. Можно настроить автономный механизм, чтобы встроить нечеткий вывод в собственный код. Все, если кодом является совместимый ANSI®.
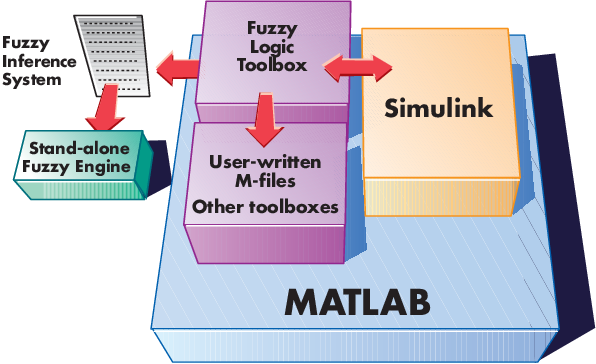
Из-за интегрированной природы среды MATLAB можно создать собственные инструменты, чтобы настроить тулбокс или использовать его с другим тулбоксом, таким как Control System Toolbox™, Deep Learning Toolbox™ или программное обеспечение Optimization Toolbox™.