Чтобы использовать GlobalSearch или решатели MultiStart, необходимо сначала создать структуру задачи. Существует два рекомендуемых способа создать структуру задачи: использование функции createOptimProblem и экспорт из приложения Оптимизации.
Выполните эти шаги, чтобы создать структуру задачи с помощью функции createOptimProblem.
Задайте свою целевую функцию как файл или анонимную функцию. Для получения дополнительной информации смотрите, Вычисляют Целевые функции. Если вашим решателем является lsqcurvefit или lsqnonlin, гарантируйте, что целевая функция возвращает вектор, не скаляр.
При необходимости создайте свои ограничения, такие как границы и нелинейные ограничительные функции. Для получения дополнительной информации смотрите Ограничения Записи.
Создайте стартовую точку. Например, чтобы создать 3D случайную стартовую точку xstart:
xstart = randn(3,1);
(Необязательно) Создайте опции с помощью optimoptions. Например,
options = optimoptions(@fmincon,'Algorithm','interior-point');
Войти
problem = createOptimProblem(solver,
где solver является именем вашего локального решателя:
Для GlobalSearch: 'fmincon'
Для MultiStart выбор:
'fmincon'
'fminunc'
'lsqcurvefit'
'lsqnonlin'
Для выбора справки см. Таблицу решений Оптимизации (Optimization Toolbox).
Установите начальную точку с помощью параметра 'x0'. Если вашей начальной точкой является xstart, и вашим решателем является fmincon, ваша запись теперь
problem = createOptimProblem('fmincon','x0',xstart,Включайте указатель на функцию для своей целевой функции в objective:
problem = createOptimProblem('fmincon','x0',xstart, ...
'objective',@objfun,Установите границы и другие ограничения как применимые.
| Ограничение | Имя |
|---|---|
| нижние границы | 'lb' |
| верхние границы | 'ub' |
матричный Aineq для линейных неравенств Aineq x ≤ bineq | 'Aineq' |
векторный bineq для линейных неравенств Aineq x ≤ bineq | 'bineq' |
матричный Aeq для линейных равенств Aeq x = beq | 'Aeq' |
векторный beq для линейных равенств Aeq x = beq | 'beq' |
| нелинейная ограничительная функция | 'nonlcon' |
При использовании lsqcurvefit локальный решатель включайте векторы входных данных и данных об ответе, названных 'xdata' и 'ydata' соответственно.
Лучшая практика: подтвердите структуру задачи путем выполнения решателя на структуре. Например, если вашим локальным решателем является fmincon:
[x,fval,eflag,output] = fmincon(problem);
Этот пример минимизирует функцию от Запущенного Решатель согласно ограничению x 1 + 2x2 ≥ 4. Цель
sixmin = 4x2 – 2.1x4 + x 6/3 + xy – 4y2 + 4y4.
Используйте алгоритм interior-point fmincon и установите стартовую точку на [2;3].
Запишите указатель на функцию для целевой функции.
sixmin = @(x)(4*x(1)^2 - 2.1*x(1)^4 + x(1)^6/3 ...
+ x(1)*x(2) - 4*x(2)^2 + 4*x(2)^4);Запишите линейные ограничительные матрицы. Измените ограничение на “меньше, чем” форма:
A = [-1,-2]; b = -4;
Создайте локальные опции, чтобы использовать алгоритм interior-point:
opts = optimoptions(@fmincon,'Algorithm','interior-point');
Создайте структуру задачи с createOptimProblem:
problem = createOptimProblem('fmincon', ...
'x0',[2;3],'objective',sixmin, ...
'Aineq',A,'bineq',b,'options',opts)Получившаяся структура:
problem =
struct with fields:
objective: @(x)(4*x(1)^2-2.1*x(1)^4+x(1)^6/3+x(1)*x(2)-4*x(2)^2+4*x(2)^4)
x0: [2x1 double]
Aineq: [-1 -2]
bineq: -4
Aeq: []
beq: []
lb: []
ub: []
nonlcon: []
solver: 'fmincon'
options: [1x1 optim.options.Fmincon]Лучшая практика: подтвердите структуру задачи путем выполнения решателя на структуре:
[x,fval,eflag,output] = fmincon(problem);
Выполните эти шаги, чтобы создать структуру задачи с помощью приложения Оптимизации.
Задайте свою целевую функцию как файл или анонимную функцию. Для получения дополнительной информации смотрите, Вычисляют Целевые функции. Если вашим решателем является lsqcurvefit или lsqnonlin, гарантируйте, что целевая функция возвращает вектор, не скаляр.
При необходимости создайте нелинейные ограничительные функции. Для получения дополнительной информации смотрите Нелинейные Ограничения (Optimization Toolbox).
Создайте стартовую точку. Например, чтобы создать 3D случайную стартовую точку xstart:
xstart = randn(3,1);
Откройте приложение Оптимизации путем ввода optimtool в командной строке, или путем выбора приложения Оптимизации из вкладки Apps.
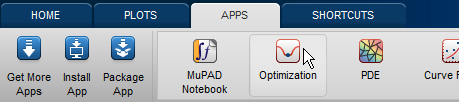
Выберите локальный Solver.

Для GlobalSearch: fmincon (значение по умолчанию).
Для MultiStart:
fmincon (значение по умолчанию)
fminunc
lsqcurvefit
lsqnonlin
Для выбора справки см. Таблицу решений Оптимизации (Optimization Toolbox).
Выберите соответствующий Algorithm. Для выбора справки смотрите Выбор Algorithm (Optimization Toolbox).

Установите начальную точку (Start point).
Включайте указатель на функцию для своей целевой функции в Objective function, и, если применимо, включайте свой Nonlinear constraint function. Например,
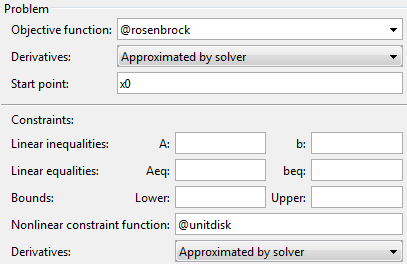
Установите границы, линейные ограничения или локальный Options. Для получения дополнительной информации на ограничениях, смотрите Ограничения Записи (Optimization Toolbox).
Лучшая практика: запустите проблему проверить настройку.
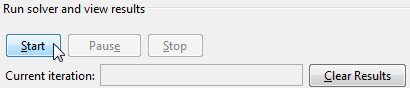
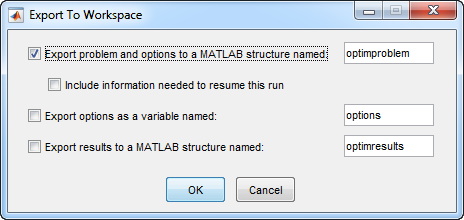
Выберите File > Export to Workspace и выберите Export problem and options to a MATLAB structure named
Этот пример минимизирует функцию от Запущенного Решатель согласно ограничению x 1 + 2x2 ≥ 4. Цель
sixmin = 4x2 – 2.1x4 + x 6/3 + xy – 4y2 + 4y4.
Используйте алгоритм interior-point fmincon и установите стартовую точку на [2;3].
Запишите указатель на функцию для целевой функции.
sixmin = @(x)(4*x(1)^2 - 2.1*x(1)^4 + x(1)^6/3 ...
+ x(1)*x(2) - 4*x(2)^2 + 4*x(2)^4);Запишите линейные ограничительные матрицы. Измените ограничение на “меньше, чем” форма:
A = [-1,-2]; b = -4;
Запустите приложение Оптимизации путем ввода optimtool в командной строке MATLAB®.
Установите решатель, алгоритм, цель, стартовую точку и ограничения.
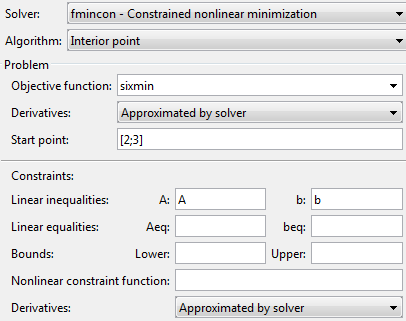
Лучшая практика: запустите проблему проверить настройку.

Проблема запускается успешно.
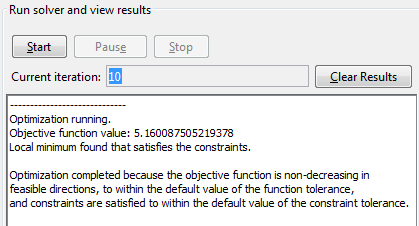
Выберите File > Export to Workspace и выберите Export problem and options to a MATLAB structure named
