Поиск и опрос

Используя метод поиска

В дополнение к опросу точек mesh алгоритм поиска шаблона может выполнить дополнительный шаг в каждой итерации, названной поиском. В каждой итерации поисковый шаг применяет другой метод оптимизации к текущей точке. Если этот поиск не улучшает текущую точку, шаг опроса выполняется.

Следующий пример иллюстрирует использование метода поиска для проблемы, описанной в Линейно Ограниченной проблеме. Чтобы настроить пример, введите следующие команды в подсказке MATLAB^®, чтобы задать начальную точку и ограничения.

x0 = [2 1 0 9 1 0];
Aineq = [-8 7 3 -4 9 0];
bineq = 7;
Aeq = [7 1 8 3 3 3; 5 0 -5 1 -5 8; -2 -6 7 1 1 9; 1 -1 2 -2 3 -3];
beq = [84 62 65 1];

Затем введите настройки, показанные в следующие фигуры в приложении Оптимизации.

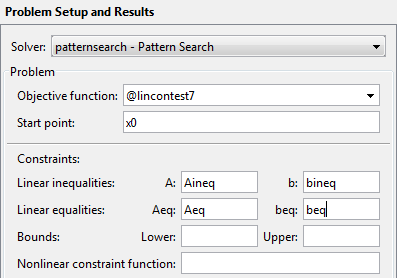
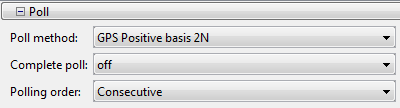
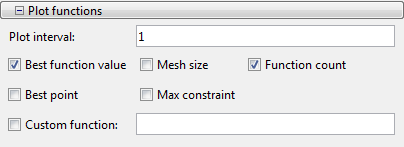
Для сравнения нажмите Start, чтобы запустить пример без метода поиска. Это отображает графики, показанные в следующей фигуре.

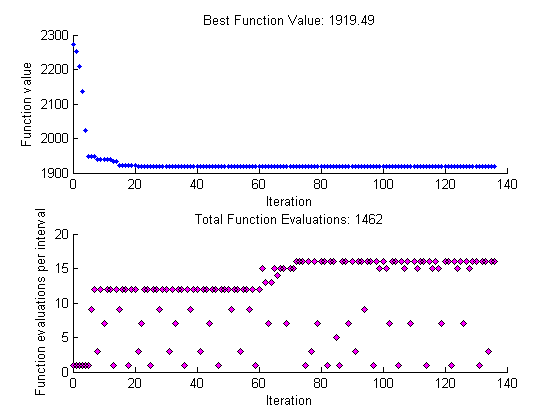
Чтобы видеть эффект использования метода поиска, выберите MADS Positive Basis 2N в поле Search method в опциях Search.

Это устанавливает метод поиска быть поиском шаблона использование шаблона для MADS Positive Basis 2N. Затем нажмите Start, чтобы запустить поиск шаблона. Это отображает следующие графики.

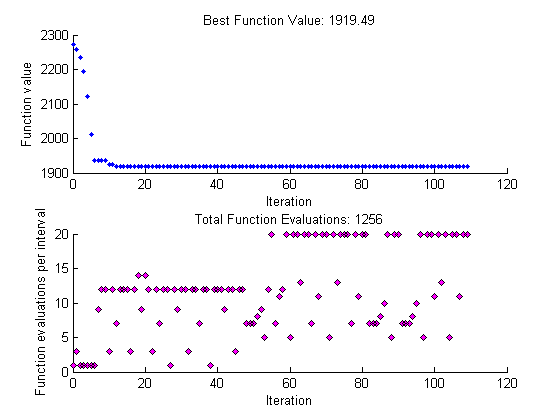
Обратите внимание на то, что использование метода поиска уменьшает общие функциональные оценки — с 1 462 до 1 256 — и сокращает количество итераций от 106 до 97.

Запускать эту проблему с помощью функций командной строки:

x0 = [2 1 0 9 1 0];
Aineq = [-8 7 3 -4 9 0];
bineq = 7;
Aeq = [7 1 8 3 3 3; 5 0 -5 1 -5 8; -2 -6 7 1 1 9; 1 -1 2 -2 3 -3];
beq = [84 62 65 1];
options = optimoptions('patternsearch',...
    'PlotFcn',{@psplotbestf,@psplotfuncount});
[x,fval] = patternsearch(@lincontest7,x0,...
    Aineq,bineq,Aeq,beq,[],[],[],options);

Чтобы использовать метод поиска MADS, измените опцию SearchFcn.

options.SearchFcn = @MADSPositiveBasis2N;
[x,fval] = patternsearch(@lincontest7,x0,...
    Aineq,bineq,Aeq,beq,[],[],[],options);

Поиск Используя другой решатель

patternsearch занимает много времени, чтобы минимизировать функцию Розенброка. Функция $f (x) = 100 {(x_{2} - x_{}^{12})}^{2} + {(1 - x_{1})}^{2} .$

Функция Розенброка описана и построена в, Решают Ограниченную Нелинейную проблему, Основанную на решателе (Optimization Toolbox).

Создайте целевую функцию.

dejong2fcn = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;

Установите опции patternsearch на MaxFunctionEvaluations = 5000 и MaxIterations = 2000:
```
opts = optimoptions('patternsearch','MaxFunctionEvaluations',5000,'MaxIterations',2000);
```
Запустите patternsearch, начинающий с [-1.9 2]:
```
[x,feval,eflag,output] = patternsearch(dejong2fcn,...
    [-1.9,2],[],[],[],[],[],[],[],opts);
```
```
Maximum number of function evaluations exceeded: increase options.MaxFunctionEvaluations.
```
```
feval
```
```
feval =
    0.8560
```
Оптимизация не завершалась, и результат не очень близко к оптимальному значению 0.
Установите опции использовать fminsearch в качестве метода поиска:
```
opts = optimoptions('patternsearch',opts,'SearchFcn',@searchneldermead);
```

Повторно выполните оптимизацию, результаты намного лучше:

[x2,feval2,eflag2,output2] = patternsearch(dejong2fcn,...
    [-1.9,2],[],[],[],[],[],[],[],opts);

Optimization terminated: mesh size less than options.MeshTolerance.

feval2

feval2 =
  4.0686e-010

fminsearch не связывается так тесно, чтобы скоординировать направления как GPS по умолчанию метод опроса patternsearch. Поэтому fminsearch более эффективен при нахождении рядом к минимуму функции Розенброка. Добавление метода поиска в этом случае является эффективным.

Документация