Функции построения графика для GlobalSearch и MultiStart

Что такое функции построения графика?

Поле PlotFcn options задает одну или несколько функций что оптимизация вызовы функции в каждой итерации. Функции построения графика строят различные меры прогресса, в то время как алгоритм выполняется. Передайте указатель на функцию или cell-массив указателей на функцию. Структура функции вывода совпадает со структурой выходной функции. Для получения дополнительной информации об этой структуре смотрите OutputFcn.

Функции построения графика являются специализированными выходными функциями (см. Выходные функции для GlobalSearch и MultiStart). Существует две предопределенных функции построения графика:

@gsplotbestf строит лучшее значение целевой функции.
@gsplotfunccount строит количество функциональных оценок.

Окна функции построения графика имеют кнопки Pause и Stop. По умолчанию все графики появляются в одном окне.

Использовать глобальные функции построения графика:

Запишите функции построения графика с помощью синтаксиса, описанного в OutputFcn.
Установите свойство PlotFcn своего объекта GlobalSearch или MultiStart к указателю на функцию вашей функции построения графика. Можно использовать несколько функций построения графика путем установки свойства PlotFcn на cell-массив указателей на функцию.

Детали встроенных функций построения графика

Встроенные функции построения графика имеют характеристики, которые могут удивить вас.

@gsplotbestf может иметь графики, которые строго не уменьшаются. Это вызвано тем, что ранние значения могут следовать из локальных выполнений решателя с отрицательными выходными флагами (такими как неосуществимые решения). Последующее локальное решение с положительным выходным флагом лучше, даже если его значение функции выше. Если локальный решатель возвращает значение с положительным выходным флагом, график является монотонным уменьшением.
@gsplotfunccount не может построить общее количество функциональных оценок. Это вызвано тем, что GlobalSearch может продолжить выполнять функциональные оценки после того, как он вызовет функцию построения графика в последний раз. Для получения дополнительной информации см. Алгоритм GlobalSearch.

Функция построения графика MultiStart

Этот пример строит количество локальных выполнений решателя, которые это берет, чтобы получить лучший локальный минимум для MultiStart. Пример также использует встроенную функцию построения графика, чтобы показать текущее лучшее значение функции.

Проблема в качестве примера эквивалентна в Глобальной переменной Находки или Нескольких Локальных Минимумах с дополнительными границами.

Пример использует персистентные переменные, чтобы сохранить предыдущие оптимальные значения. Функция построения графика исследует лучшее значение функции после каждого локального решателя, запущенного, доступного в поле bestfval структуры optimValues. Если значение не ниже, чем предыдущее лучшее, функция построения графика добавляет 1 в количество последовательных вызовов без улучшения и чертит столбчатую диаграмму. Если значение ниже, чем предыдущее лучшее, функция построения графика запускает новую панель в графике со значением 1. Перед графическим выводом функция построения графика взяла логарифм количества последовательных вызовов. Логарифм помогает сохранить график четким, поскольку некоторые значения могут быть намного больше, чем другие.

Чтобы сохранить локальные результаты с помощью вложенных функций вместо персистентных переменных, смотрите Пример Вложенной Выходной функции (MATLAB).

Запишите целевую функцию:

function f = sawtoothxy(x,y)
[t r] = cart2pol(x,y); % change to polar coordinates
h = cos(2*t - 1/2)/2 + cos(t) + 2;
g = (sin(r) - sin(2*r)/2 + sin(3*r)/3 - sin(4*r)/4 + 4) ...
    .*r.^2./(r+1);
f = g.*h;

Сохраните sawtoothxy.m как файл в папке на вашем пути MATLAB^®.

Запишите функцию построения графика:

function stop = NumberToNextBest(optimValues, state)

persistent bestfv bestcounter

stop = false;
switch state
    case 'init'
        % Initialize variable to record best function value.
        bestfv = []; 
        
        % Initialize counter to record number of
        % local solver runs to find next best minimum.
        bestcounter = 1; 
        
        % Create the histogram.
        bar(log(bestcounter),'tag','NumberToNextBest');
        xlabel('Number of New Best Fval Found');
        ylabel('Log Number of Local Solver Runs');
        title('Number of Local Solver Runs to Find Lower Minimum')
    case 'iter'
        % Find the axes containing the histogram.
        NumToNext = ...
          findobj(get(gca,'Children'),'Tag','NumberToNextBest');
        
        % Update the counter that records number of local
        % solver runs to find next best minimum.
        if ~isequal(optimValues.bestfval, bestfv)
            bestfv = optimValues.bestfval;
            bestcounter = [bestcounter 1];
        else
            bestcounter(end) = bestcounter(end) + 1;
        end
        
        % Update the histogram.
        set(NumToNext,'Ydata',log(bestcounter))
end

Сохраните NumberToNextBest.m как файл в папке на вашем пути MATLAB.
Создайте структуру задачи и глобальный решатель. Установите нижние границы [-3e3,-4e3], верхние границы [4e3,3e3] и установите глобальный решатель использовать функции построения графика:
```
problem = createOptimProblem('fmincon',...
    'objective',@(x)sawtoothxy(x(1),x(2)),...
    'x0',[100,-50],'lb',[-3e3 -4e3],...
    'ub',[4e3,3e3],'options',...
    optimoptions(@fmincon,'Algorithm','sqp'));

ms = MultiStart('PlotFcn',{@NumberToNextBest,@gsplotbestf});
```
Запустите глобальный решатель для 100 локальных выполнений решателя:
```
[x,fv] = run(ms,problem,100);
```
Функции построения графика производят следующую фигуру (ваши результаты могут отличаться, поскольку процесс решения является стохастическим):

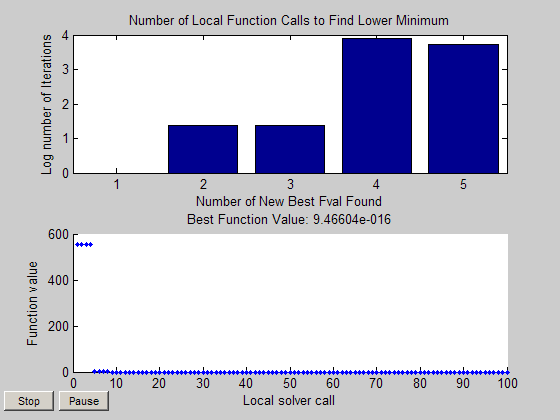
Никакие параллельные функции построения графика

В то время как MultiStart может запуститься параллельно, он не поддерживает функции мирового производства и функции построения графика параллельно. Кроме того, в то время как локальные выходные функции и функции построения графика работают на рабочих, когда MultiStart запускается параллельно, эффект отличается от выполнения последовательно. Локальный вывод и функции построения графика не создают отображение при работе рабочих. Вы не видите никаких других эффектов вывода и функций построения графика, пока рабочий не передает его результаты клиенту (инициатор заданий параллели MultiStart).

Для получения информации о выполнении MultiStart параллельно, смотрите Параллельные вычисления.

Документация