GlobalSearch и MultiStart имеют аналогичные подходы к нахождению глобальной переменной или нескольких минимумов. Оба алгоритма запускают локальный решатель (такой как fmincon) от нескольких стартовых точек. Алгоритмы используют несколько стартовых точек, чтобы выбрать несколько бассейнов привлекательности. Для получения дополнительной информации смотрите Бассейны Привлекательности.
Обзор Алгоритма GlobalSearch и MultiStart содержит эскиз алгоритмы MultiStart и GlobalSearch.
GlobalSearch и обзор алгоритма MultiStart
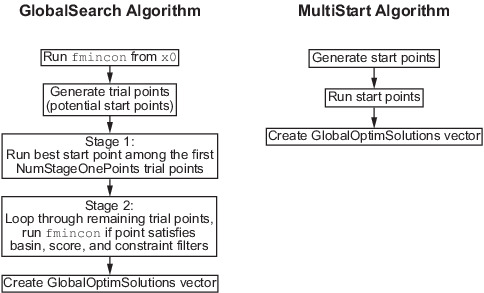
Основные отличия между GlobalSearch и MultiStart:
GlobalSearch использует поисковый рассеянием механизм для генерации стартовых точек. MultiStart использует равномерно распределенные стартовые точки в границах или предоставленные пользователями стартовые точки.
GlobalSearch анализирует стартовые точки и отклоняет те точки, которые вряд ли улучшат лучший локальный минимум, найденный до сих пор. MultiStart запускает все стартовые точки (или, опционально, все стартовые точки, которые выполнимы относительно границ или ограничений неравенства).
MultiStart дает выбор локального решателя: fmincon, fminunc, lsqcurvefit или lsqnonlin. Алгоритм GlobalSearch использует fmincon.
MultiStart может запуститься параллельно, распределительные стартовые точки к нескольким процессорам для локального решения. Чтобы запустить MultiStart параллельно, смотрите, Как Использовать Параллельную обработку в Global Optimization Toolbox.
Различия между этими объектами решателя сводятся к следующему решению, на котором можно использовать:
Используйте GlobalSearch, чтобы найти один глобальный минимум наиболее эффективно на одном процессоре.
Используйте MultiStart для:
Найдите несколько локальных минимумов.
RunInParallel.
Используйте решатель кроме fmincon.
Поиск полностью глобального минимума.
Исследуйте свои собственные стартовые точки.
Для описания алгоритма смотрите Ugray и др. [1].
Когда вы run объект GlobalSearch, алгоритм выполняет следующие шаги:
GlobalSearch запускает fmincon от стартовой точки, которую вы даете в структуре problem. Если это выполнение сходится, GlobalSearch записывает стартовую точку и конечную точку для первоначальной оценки на радиусе бассейна привлекательности. Кроме того, GlobalSearch записывает итоговое значение целевой функции для использования в функции score (см., Получают Стартовую точку Этапа 1, Выполнение).
Функция счета является суммой значения целевой функции в точке и кратном сумме ограничительных нарушений. Таким образом, допустимая точка имеет счет, равный его значению целевой функции. Несколько для ограничительных нарушений первоначально 1000. GlobalSearch обновляет несколько во время выполнения.
GlobalSearch использует поля точек алгоритм поиска, чтобы сгенерировать набор испытательных точек NumTrialPoints. Испытательные точки являются потенциальными стартовыми точками. Для описания поля точек алгоритма поиска смотрите Перчаточника [2]. GlobalSearch генерирует испытательные точки в любых конечных границах, которые вы устанавливаете (lb и ub). Неограниченным компонентам наложили искусственные границы: lb = -1e4 + 1, ub = 1e4 + 1. Эта область значений не симметрична вокруг начала координат так, чтобы источник не был в поля точек поиске. Компонентам с односторонними границами наложили искусственные границы на неограниченную сторону, переключенную конечными границами, чтобы сохранить lb < ub.
GlobalSearch выполняет функцию счета набора испытательных точек NumStageOnePoints. Это затем берет точку с лучшим счетом и запускает fmincon от той точки. GlobalSearch удаляет набор испытательных точек NumStageOnePoints из его списка точек, чтобы исследовать.
localSolverThreshold является первоначально меньшими из двух значений целевой функции в точках решения. Точки решения являются решениями fmincon, начинающими с x0 и со стартовой точки Этапа 1. Если обе из этих точек решения не существуют или неосуществимы, localSolverThreshold является первоначально значением функции штрафа стартовой точки Этапа 1.
Предположение эвристики GlobalSearch - то, что бассейны привлекательности являются сферическими. Первоначальная оценка бассейнов привлекательности для точки решения от x0 и точки решения от Этапа 1 является сферами, сосредоточенными в точках решения. Радиус каждой сферы является расстоянием от начальной точки до точки решения. Эти предполагаемые бассейны могут наложиться.
Существует два набора счетчиков, сопоставленных с алгоритмом. Каждый счетчик является количеством последовательных испытательных точек что:
Лгите в бассейне привлекательности. Существует один счетчик для каждого бассейна.
Имейте функцию счета, больше, чем localSolverThreshold. Для определения счета смотрите Выполнение fmincon от x0.
Все счетчики первоначально 0.
GlobalSearch неоднократно исследует остающуюся испытательную точку из списка и выполняет следующие шаги. Это постоянно контролирует время и останавливает поиск, если прошедшее время превышает секунды MaxTime.
Вызовите испытательную точку p. Запустите fmincon от p, если следующие условия содержат:
p не находится ни в каком существующем бассейне. Критерий каждого бассейна i:
|p - center(i)| > DistanceThresholdFactor * radius(i).
DistanceThresholdFactor является опцией (значение по умолчанию 0.75).
radius является предполагаемым радиусом, который обновляет в Радиусе Бассейна с Обновлением и Пороге, и Реагируйте на Большие Встречные Значения.
выиграйте (p) <localSolverThreshold.
(дополнительный) p удовлетворяет связанные и/или ограничения неравенства. Этот тест происходит, если вы устанавливаете свойство StartPointsToRun объекта GlobalSearch к 'bounds' или 'bounds-ineqs'.
Сбросьте счетчики
Установите счетчики для бассейнов и порога к 0.
Обновите набор решения
Если выполнения fmincon, начинающие с p, это может привести к положительному выходному флагу, который указывает на сходимость. В этом случае GlobalSearch обновляет вектор объектов GlobalOptimSolution. Вызовите точку решения xp и значение целевой функции fp. Существует два случая:
Поскольку любое решение указывает xq со значением целевой функции fq,
|xq - xp| > XTolerance * max(1,|xp|)
или
|fq - fp| > FunctionTolerance * max(1,|fp|).
В этом случае GlobalSearch создает новый элемент в векторе объектов GlobalOptimSolution. Для получения дополнительной информации информации, содержавшейся в каждом объекте, смотрите GlobalOptimSolution.
Поскольку некоторое другое решение указывает xq со значением целевой функции fq,
|xq - xp| <= XTolerance * max(1,|xp|)
и
|fq - fp| <= FunctionTolerance * max(1,|fp|).
В этом случае GlobalSearch рассматривает xp как эквивалентный xq. Алгоритм GlobalSearch изменяет GlobalOptimSolution xq путем добавления p в массив ячеек точек X0.
Существует одна незначительная тонкая настройка, которая может произойти с этим обновлением. Если выходной флаг для xq больше, чем 1, и выходным флагом для xp является 1, то xp заменяет xq. Эта замена может привести к некоторым точкам в том же бассейне, являющемся больше, чем расстояние XTolerance от xp.
Обновите радиус бассейна и порог
Если выходной флаг текущего запущенного fmincon положителен:
Установите порог к значению счета в стартовой точке p.
Установите радиус бассейна для xp, равного максимуму существующего радиуса (если таковые имеются) и расстояние между p и xp.
Сообщите итеративному отображению
Когда свойством GlobalSearch Display является 'iter', каждая точка, что выполнения fmincon создают одну строку в GlobalSearch итеративное отображение.
Обновите счетчики
Постепенно увеличьте счетчик для каждого бассейна, содержащего p. Сбросьте счетчик любого бассейна к 0.
Постепенно увеличьте пороговый счетчик если счет (p) > = localSolverThreshold. В противном случае сбросьте в противоречии с 0.
Реагируйте на большие встречные значения
Для каждого бассейна со счетчиком, равным MaxWaitCycle, умножьте радиус бассейна на 1 – BasinRadiusFactor. Сбросьте в противоречии с 0. (И MaxWaitCycle и BasinRadiusFactor являются устанавливаемыми свойствами объекта GlobalSearch.)
Если пороговый счетчик равняется MaxWaitCycle, увеличьте порог:
новый порог = порог + PenaltyThresholdFactor* (1 + abs (порог)).
Сбросьте в противоречии с 0.
Сообщите итеративному отображению
Каждая 200-я испытательная точка создает одну строку в GlobalSearch итеративное отображение.
После достижения секунд MaxTime или исчерпывания испытательных точек, GlobalSearch создает вектор объектов GlobalOptimSolution. GlobalSearch заказывает вектор значением целевой функции от самого низкого (лучше всего) к (худшему) самому высокому. Это завершает алгоритм.
Когда вы run объект MultiStart, алгоритм выполняет следующие шаги:
MultiStart проверяет входные параметры на валидность. Проверки включают выполнение локального решателя однажды на проблемных входных параметрах. Даже когда запущено параллельно, MultiStart выполняет эти проверки последовательно.
Если вы вызываете MultiStart с синтаксисом
[x,fval] = run(ms,problem,k)
для целочисленного k MultiStart генерирует стартовые точки k - 1 точно, как будто вы использовали объект RandomStartPointSet. Алгоритм также использует стартовую точку x0 от структуры problem в общей сложности для стартовых точек k.
Объект RandomStartPointSet не имеет никаких точек сохраненными в объекте. Вместо этого MultiStart вызывает list, который генерирует случайные точки в границах, данных структурой problem. Если неограниченный компонент существует, list использует искусственное, связанное данный свойством ArtificialBound объекта RandomStartPointSet.
Если вы обеспечиваете объект CustomStartPointSet, MultiStart не генерирует стартовые точки, но использует точки в объекте.
Если вы устанавливаете свойство StartPointsToRun объекта MultiStart к 'bounds' или 'bounds-ineqs', MultiStart не запускает локальный решатель от неосуществимых стартовых точек. В этом контексте, “неосуществимом”, означает стартовые точки, которые не удовлетворяют границы или стартовые точки, которые не удовлетворяют и границы и ограничения неравенства.
Настройкой по умолчанию StartPointsToRun является 'all'. В этом случае MultiStart не отбрасывает неосуществимые стартовые точки.
MultiStart запускает локальный решатель, заданный в problem.solver, запускающемся в точках, которые передают фильтр StartPointsToRun. Если MultiStart запускается параллельно, он отправляет стартовые точки в процессоры рабочего по одному, и процессоры рабочего запускают локальный решатель.
Локальный решатель проверяет, протекли ли секунды MaxTime в каждой из его итераций. Если так, это выходит из той итерации, не сообщая о решении.
Когда локальный решатель останавливается, MultiStart хранит результаты и продолжается к следующему шагу.
Сообщите Итеративному Отображению. Когда свойством MultiStart Display является 'iter', каждая точка, что локальные выполнения решателя создают одну строку в MultiStart итеративное отображение.
MultiStart останавливается, когда он исчерпывает стартовые точки. Это также останавливается, когда это превышает общее время выполнения секунд MaxTime.
После того, как MultiStart достигает останавливающегося условия, алгоритм создает вектор объектов GlobalOptimSolution можно следующим образом:
Сортировка локальных решений значением целевой функции (Fval) от самого низкого до самого высокого. Для lsqnonlin и lsqcurvefit локальные решатели, целевая функция является нормой невязки.
Цикл по локальным решениям j, начинающийся с самого низкого (лучшего) Fval.
Найдите все решения k, удовлетворяющим обоих:
|Fval(k) - Fval(j)| <= FunctionTolerance*max(1,|Fval(j)|)
|x(k) - x(j)| <= XTolerance*max(1,|x(j)|)
Запишите j, Fval(j), локальный решатель структура output для j и массив ячеек стартовых точек для j и всего k. Удалите те точки k из списка локальных решений. Эта точка является одной записью в векторе объектов GlobalOptimSolution.
Итоговый вектор объектов GlobalOptimSolution в порядке Fval от самого низкого (лучше всего) к (худшему) самому высокому.
Сообщите Итеративному Отображению. После исследования всех локальных решений MultiStart дает сводные данные итеративному отображению. Эти сводные данные включают количество локальных выполнений решателя, которые сходились, номер, которому не удалось сходиться, и номер, который имел ошибки.
[1] Ugray, Zsolt, Леон Лэсдон, Джон К. Пламмер, Фред Гловер, Джеймс Келли и Рафаэль Марти. Рассейте Поиск и Локальные Решатели NLP: A Мультизапускают Среду для Глобальной Оптимизации. Журнал INFORMS на Вычислении, Издании 19, № 3, 2007, стр 328–340.
[2] Перчаточник, F. “Шаблон для поля точек поиска и пересоединения пути”. Искусственная Эволюция (J.-K. Хао, E.Lutton, E.Ronald, M.Schoenauer, D.Snyers, редакторы). Читайте лекции Примечаниям в Информатике, 1363, Спрингер, Берлине/Гейдельберге, 1998, стр 13–54.
[3] Диксон, L. и Г. П. Сзеге. “Глобальная Задача оптимизации: Введение”. К Глобальной Оптимизации 2 (Диксон, L. C. W. и Г. П. Сзеге, редакторы). Амстердам, Нидерланды: Северная Голландия, 1978.