Документация

Важность разнообразия генеральной совокупности

Один из наиболее важных факторов, который определяет производительность генетического алгоритма, выполняет, разнообразие генеральной совокупности. Если среднее расстояние между людьми является большим, разнообразие высоко; если среднее расстояние мало, разнообразие является низким. Получение правильной суммы разнообразия является вопросом запуска и ошибки. Если разнообразие является слишком высоким или слишком низким, генетический алгоритм не может выполнить хорошо.

Этот раздел объясняет, как управлять разнообразием путем установки Initial range генеральной совокупности. Установка Объема Мутации описывает, как объем мутации влияет на разнообразие.

Этот раздел также объясняет, как установить численность населения.

Установка начальной области значений

По умолчанию ga создает случайную начальную генеральную совокупность, использующую функцию создания. Можно задать область значений векторов в начальной генеральной совокупности в поле Initial range в опциях Population.

Если вы знаете приблизительно, где решение проблемы находится, задайте начальную область значений так, чтобы это содержало ваше предположение для решения. Однако генетический алгоритм может найти решение, даже если это не находится в начальном диапазоне, если у генеральной совокупности есть достаточно разнообразия.

Следующий пример показывает, как начальная область значений влияет на производительность генетического алгоритма. Пример использует функцию Рэстриджина, описанный в Минимизируют Функцию Рэстриджина. Минимальное значение функции 0, который происходит в начале координат.

Чтобы запустить пример, откройте решатель ga в приложении Оптимизации путем ввода optimtool('ga') в командной строке. Установите следующее:

Нажмите Start in Run solver and view results. Несмотря на то, что результаты вычислений генетического алгоритма случайны, ваши результаты подобны следующей фигуре с лучшим значением функции фитнеса приблизительно 2.

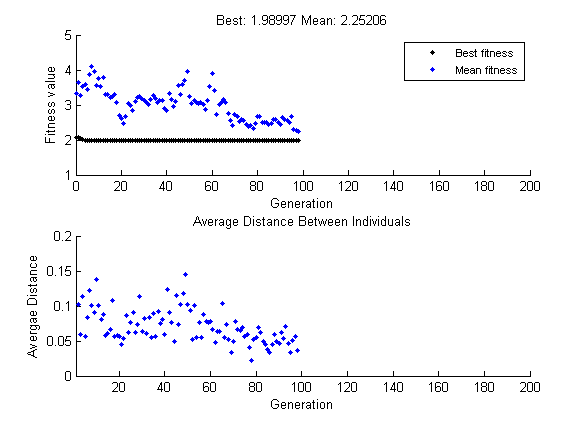
Верхний график, который отображает лучший фитнес при каждой генерации, показывает небольшой прогресс понижения значения фитнеса. Более низкий график показывает среднее расстояние между людьми при каждой генерации, которая является хорошей мерой разнообразия генеральной совокупности. Для этой установки начальной области значений существует слишком мало разнообразия для алгоритма, чтобы сделать успехи.

Запускать эту проблему с помощью функций командной строки:

options = optimoptions('ga','InitialPopulationRange',[1;1.1],...
    'PlotFcn',{@gaplotbestf,@gaplotdistance});
x = ga(@rastriginsfcn,2,[],[],[],[],[],[],[],options)

Затем, попробуйте установку Initial range к [1;100] и выполнение алгоритма. На этот раз результатами является больше переменной. Вы можете получить график с лучшим значением фитнеса приблизительно 7, как в следующем графике. Вы можете получить различные результаты.

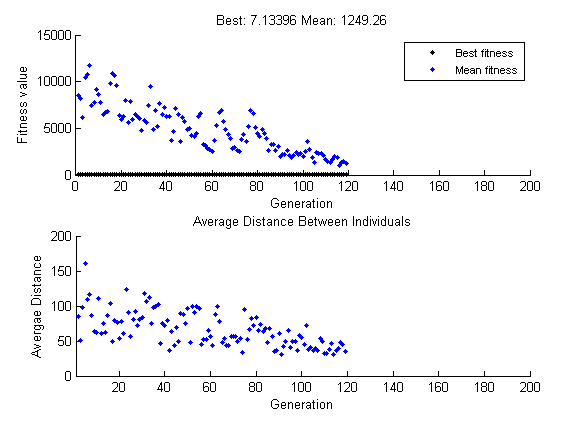
На этот раз генетический алгоритм делает успехи, но потому что среднее расстояние между людьми является настолько большим, лучшие люди далеки от оптимального решения.

Запускать эту проблему с помощью функций командной строки:

options = optimoptions('ga','InitialPopulationRange',[1;100],...
    'PlotFcn',{@gaplotbestf,@gaplotdistance});
x = ga(@rastriginsfcn,2,[],[],[],[],[],[],[],options)

Наконец, установите Initial range на [1;2] и запустите генетический алгоритм. Снова, в результате существует изменчивость, но вы можете получить результат, подобный следующей фигуре. Запускайте оптимизацию несколько раз, и вы в конечном счете получаете конечный пункт около [0;0] со значением функции фитнеса около 0.

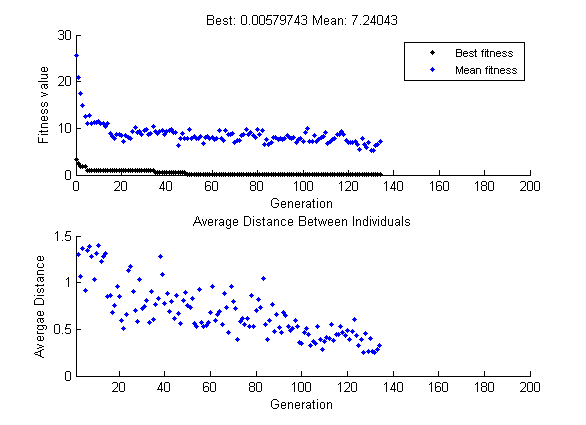
Разнообразие в этом случае лучше подходит для проблемы, таким образом, ga обычно возвращает лучший результат, чем в предыдущих двух случаях.

Запускать эту проблему с помощью функций командной строки:

options = optimoptions('ga','InitialPopulationRange',[1;2],...
    'PlotFcn',{@gaplotbestf,@gaplotdistance});
x = ga(@rastriginsfcn,2,[],[],[],[],[],[],[],options)

Пользовательская функция построения графика и линейные ограничения в ga

Этот пример показывает, как @gacreationlinearfeasible, функция создания по умолчанию для линейно ограниченных проблем, создает генеральную совокупность для ga. Генеральная совокупность хорошо рассеивается и смещается, чтобы лечь на ограничительные контуры. Пример использует пользовательскую функцию построения графика.

function state = gaplotshowpopulation2(~,state,flag,fcn)
%gaplotshowpopulation2 Plots the population and linear constraints in 2-d.
%   STATE = gaplotshowpopulation2(OPTIONS,STATE,FLAG) plots the population
%   in two dimensions.
%
%   Example:
%     fun = @lincontest6;
%     options = gaoptimset('PlotFcn',{{@gaplotshowpopulation2,fun}});
%     [x,fval,exitflag] = ga(fun,2,A,b,[],[],lb,[],[],options);

% This plot function works in 2-d only
if size(state.Population,2) > 2
    return;
end
if nargin < 4
    fcn = [];
end
% Dimensions to plot
dimensionsToPlot = [1 2];

switch flag
    % Plot initialization
    case 'init'
        pop = state.Population(:,dimensionsToPlot);
        plotHandle = plot(pop(:,1),pop(:,2),'*');
        set(plotHandle,'Tag','gaplotshowpopulation2')
        title('Population plot in two dimension','interp','none')
        xlabelStr = sprintf('%s %s','Variable ', num2str(dimensionsToPlot(1)));
        ylabelStr = sprintf('%s %s','Variable ', num2str(dimensionsToPlot(2)));
        xlabel(xlabelStr,'interp','none');
        ylabel(ylabelStr,'interp','none');
        hold on;
       
        % plot the inequalities
        plot([0 1.5],[2 0.5],'m-.') %  x1 + x2 <= 2
        plot([0 1.5],[1 3.5/2],'m-.'); % -x1 + 2*x2 <= 2
        plot([0 1.5],[3 0],'m-.'); % 2*x1 + x2 <= 3
        % plot lower bounds
        plot([0 0], [0 2],'m-.'); % lb = [ 0 0];
        plot([0 1.5], [0 0],'m-.'); % lb = [ 0 0];
        set(gca,'xlim',[-0.7,2.2])
        set(gca,'ylim',[-0.7,2.7])
        axx = gcf;
        % Contour plot the objective function
        if ~isempty(fcn)
            range = [-0.5,2;-0.5,2];
            pts = 100;
            span = diff(range')/(pts - 1);
            x = range(1,1): span(1) : range(1,2);
            y = range(2,1): span(2) : range(2,2);

            pop = zeros(pts * pts,2);
            values = zeros(pts,1);
            k = 1;
            for i = 1:pts
                for j = 1:pts
                    pop(k,:) = [x(i),y(j)];
                    values(k) = fcn(pop(k,:));
                    k = k + 1;
                end
            end
            values = reshape(values,pts,pts);
            contour(x,y,values);
            colorbar
        end
        % Show the initial population
        ax = gca;
        fig = figure;
        copyobj(ax,fig);colorbar
        % Pause for three seconds to view the initial plot, then resume
        figure(axx)
        pause(3);
    case 'iter'
        pop = state.Population(:,dimensionsToPlot);
        plotHandle = findobj(get(gca,'Children'),'Tag','gaplotshowpopulation2');
        set(plotHandle,'Xdata',pop(:,1),'Ydata',pop(:,2));
end

A = [1,1;-1,2;2,1];
b = [2;2;3];
lb = zeros(2,1);

options = optimoptions('ga','PlotFcns',...
{{@gaplotshowpopulation2,@lincontest6}});

rng default % for reproducibility
[x,fval] = ga(@lincontest6,2,A,b,[],[],lb,[],[],options);

Optimization terminated: average change in the fitness value less than options.FunctionTolerance.

Установка численности населения

Поле Population size в опциях Population определяет размер генеральной совокупности при каждой генерации. Увеличение численности населения позволяет генетическому алгоритму искать больше точек и таким образом получить лучший результат. Однако, чем больше численность населения, тем дольше генетический алгоритм берет, чтобы вычислить каждую генерацию.

Можно экспериментировать с различными настройками для Population size, которые возвращают хорошие результаты, не занимая препятствующее количество времени, чтобы запуститься.