Можно построить моделируемый ответ модели с помощью импульса и продвинуться сигналы как вход для всех линейных параметрических моделей и корреляционного анализа (непараметрические) модели.
Можно также создать переходные процессы для нелинейных моделей. Они продвигаются и посылают импульсы графики ответа, также названные переходными графиками ответа, обеспечивают понимание характеристик образцовой динамики, включая максимальную чувствительность и время установления.
Для моделей частотной характеристики импульс - и переходные процессы не доступен. Для нелинейных моделей только переходные процессы доступны.
Переходные графики ответа обеспечивают понимание основных динамических свойств модели, таких как время отклика, статические усиления и задержки.
Переходные графики ответа также помогают вам подтвердить, как хорошо линейная параметрическая модель, такая как линейная модель ARX или модель в пространстве состояний, получает динамику. Например, можно оценить импульс или переходной процесс от данных с помощью корреляционного анализа (непараметрическая модель), и затем построить результат корреляционного анализа сверх переходных ответов параметрических моделей.
Поскольку непараметрические и параметрические модели выведены с помощью различных алгоритмов, соглашения между этими увеличениями моделей уверенность в параметрических образцовых результатах.
Переходные графики ответа показывают значение импульса или переходного процесса на вертикальной оси. Горизонтальная ось находится в модулях времени, которое вы задали для данных, используемых, чтобы оценить модель.
Импульсный ответ динамической модели является выходным сигналом, который заканчивается, когда вход является импульсом. Таким образом, u (t) является нулем для всех значений t кроме в t=0, где u (0) =1. В следующем разностном уравнении можно вычислить импульсный ответ установкой y (-T) =y (-2T) =0, u (0) =1, и u (t> 0) =0.
Переходной процесс является выходным сигналом, который следует из входа шага, где u (t <0) =0 и u (t> 0) =1.
Если ваша модель включает шумовую модель, можно отобразить переходный ответ шумовой модели, сопоставленной с каждым выходным каналом. Для получения дополнительной информации о том, как отобразить переходный ответ шумовой модели, смотрите Импульс Графика и Переходной процесс Используя Приложение System Identification.
Следующие данные показывают демонстрационный Переходный график Ответа, созданный в приложении System Identification.
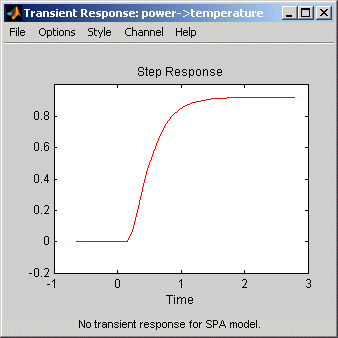
В дополнение к переходной кривой отклика можно отобразить доверительный интервал на графике. Чтобы изучить, как показать или скрыть доверительный интервал, см. описание настроек графика в Импульсе Графика и Переходном процессе Используя Приложение System Identification.
Доверительный интервал соответствует области значений значений ответа с определенной вероятностью того, чтобы быть фактическим ответом системы. Тулбокс использует оцененную неопределенность в параметрах модели, чтобы вычислить доверительные интервалы и принимает, что оценки имеют Распределение Гаусса.
Например, для 95%-го доверительного интервала, область вокруг номинальной кривой представляет область значений, где существует 95%-й шанс, что это содержит истинный отклик системы. Можно задать доверительный интервал как вероятность (между 0 и 1) или как количество стандартных отклонений Распределения Гаусса. Например, вероятность 0,99 (99%) соответствует 2,58 стандартным отклонениям.
Вычисление доверительного интервала принимает, что модель достаточно описывает системную динамику, и образцовые невязки проходят тесты независимости.