Эта тема описывает функции, которые выполняют просачивание частотного диапазона. Для получения информации о разработке просачивается пространственная область, смотрите то, Что Изображение, Просачивающееся Пространственная Область?.
Программное обеспечение Image Processing Toolbox™ поддерживает один класс линейного фильтра: двумерный фильтр конечного импульсного ответа (FIR). КИХ-фильтры имеют конечную степень к одной точке или импульс. Все функции проекта фильтра Image Processing Toolbox возвращают КИХ-фильтры.
КИХ-фильтры имеют несколько характеристик, которые делают их идеальными для обработки изображений в среде MATLAB®:
КИХ-фильтры легко представлять как матрицы коэффициентов.
Двумерные КИХ-фильтры являются естественными расширениями одномерных КИХ-фильтров.
Существует несколько известных, надежных методов для КИХ-проекта фильтра.
КИХ-фильтры легко реализовать.
КИХ-фильтры могут быть разработаны, чтобы иметь линейную фазу, которая помогает предотвратить искажение.
Другой класс фильтра, фильтра бесконечного импульсного ответа (IIR), столь же не подходит для приложений для обработки изображений. Это испытывает недостаток в свойственной устойчивости и простоте разработки и реализации КИХ-фильтра. Поэтому этот тулбокс не оказывает БИХ-поддержку фильтра.
Большинство методов разработки, описанных в этом разделе, работает путем создания двумерного фильтра из одномерного фильтра или окна, созданного с помощью функций Signal Processing Toolbox. Несмотря на то, что этот тулбокс не требуется, вы можете найти трудным разработать фильтры, если у вас нет программного обеспечения Signal Processing Toolbox.
Этот пример показывает, как преобразовать одномерный КИХ-фильтр в двумерный КИХ-фильтр с помощью функции ftrans2. Эта функция может быть полезной, потому что легче разработать одномерный фильтр с конкретными характеристиками, чем соответствующий двумерный фильтр. Метод преобразования частоты сохраняет большинство характеристик одномерного фильтра, особенно пропускная способность перехода и характеристики пульсации. Форма одномерной частотной характеристики явно очевидна в двумерном ответе.
Эта функция использует матрицу преобразования, набор элементов, который задает преобразование частоты. Матрица преобразования этой функции по умолчанию производит фильтры почти с круговой симметрией. Путем определения собственной матрицы преобразования можно получить различные симметрии. (См. Джэ С. Лима, Двумерную Обработку сигналов и Обработку изображений, 1990, для деталей.)
Создайте 1D КИХ-фильтр с помощью функции firpm от Signal Processing Toolbox™.
b = firpm(10,[0 0.4 0.6 1],[1 1 0 0])
b =
Columns 1 through 9
0.0537 -0.0000 -0.0916 -0.0001 0.3131 0.4999 0.3131 -0.0001 -0.0916
Columns 10 through 11
-0.0000 0.0537Преобразуйте 1D фильтр к 2D фильтру.
h = ftrans2(b);
h =
Columns 1 through 9
0.0001 0.0005 0.0024 0.0063 0.0110 0.0132 0.0110 0.0063 0.0024
0.0005 0.0031 0.0068 0.0042 -0.0074 -0.0147 -0.0074 0.0042 0.0068
0.0024 0.0068 -0.0001 -0.0191 -0.0251 -0.0213 -0.0251 -0.0191 -0.0001
0.0063 0.0042 -0.0191 -0.0172 0.0128 0.0259 0.0128 -0.0172 -0.0191
0.0110 -0.0074 -0.0251 0.0128 0.0924 0.1457 0.0924 0.0128 -0.0251
0.0132 -0.0147 -0.0213 0.0259 0.1457 0.2021 0.1457 0.0259 -0.0213
0.0110 -0.0074 -0.0251 0.0128 0.0924 0.1457 0.0924 0.0128 -0.0251
0.0063 0.0042 -0.0191 -0.0172 0.0128 0.0259 0.0128 -0.0172 -0.0191
0.0024 0.0068 -0.0001 -0.0191 -0.0251 -0.0213 -0.0251 -0.0191 -0.0001
0.0005 0.0031 0.0068 0.0042 -0.0074 -0.0147 -0.0074 0.0042 0.0068
0.0001 0.0005 0.0024 0.0063 0.0110 0.0132 0.0110 0.0063 0.0024
Columns 10 through 11
0.0005 0.0001
0.0031 0.0005
0.0068 0.0024
0.0042 0.0063
-0.0074 0.0110
-0.0147 0.0132
-0.0074 0.0110
0.0042 0.0063
0.0068 0.0024
0.0031 0.0005
0.0005 0.0001Просмотрите частотную характеристику фильтров.
[H,w] = freqz(b,1,64,'whole');
colormap(jet(64))
plot(w/pi-1,fftshift(abs(H)))
figure, freqz2(h,[32 32])
Одномерная частотная характеристика
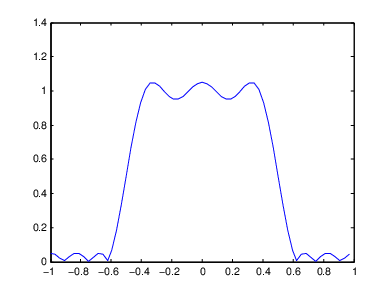
Соответствующая двумерная частотная характеристика
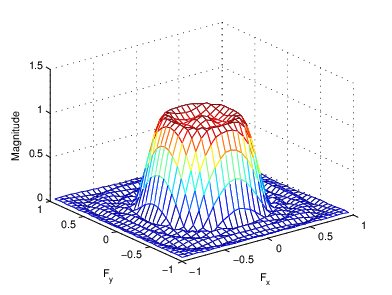
Метод выборки частоты создает фильтр на основе желаемой частотной характеристики. Учитывая матрицу точек, которые задают форму частотной характеристики, этот метод создает фильтр, частотная характеристика которого проходит через те точки. Выборка частоты не помещает ограничений на поведение частотной характеристики между данными точками; обычно, ответ слегка колеблется в этих областях. (Пульсации являются колебаниями вокруг постоянного значения. Частотная характеристика практического фильтра часто имеет пульсации, где частотная характеристика идеального фильтра является плоской.)
Функция тулбокса fsamp2 реализует проект выборки частоты для двумерных КИХ-фильтров. fsamp2 возвращает фильтр h с частотной характеристикой, которая проходит через точки во входной матрице Hd. Пример ниже создает 11 11 фильтр с помощью fsamp2 и строит частотную характеристику получившегося фильтра. (Функция freqz2 в этом примере вычисляет двумерную частотную характеристику фильтра. Смотрите Вычисление Частотной характеристики Фильтра для получения дополнительной информации.)
Hd = zeros(11,11); Hd(4:8,4:8) = 1; [f1,f2] = freqspace(11,'meshgrid'); mesh(f1,f2,Hd), axis([-1 1 -1 1 0 1.2]), colormap(jet(64)) h = fsamp2(Hd); figure, freqz2(h,[32 32]), axis([-1 1 -1 1 0 1.2])
Желаемая двумерная частотная характеристика (слева) и фактическая двумерная частотная характеристика (справа)
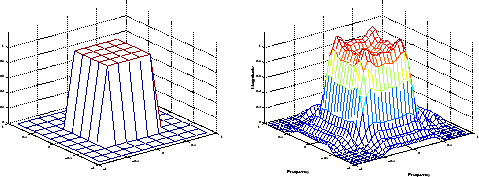
Заметьте пульсации в фактической частотной характеристике, по сравнению с желаемой частотной характеристикой. Эти пульсации являются основной проблемой с частотой, выбирающей метод разработки. Они происходят везде, где существуют резкие переходы в желаемом ответе.
Можно уменьшать пространственную степень пульсаций при помощи более крупного фильтра. Однако более крупный фильтр не уменьшает высоту пульсаций и требует большего количества времени вычисления для фильтрации. Чтобы достигнуть более сглаженного приближения к желаемой частотной характеристике, рассмотрите использование метода преобразования частоты или метода работы с окнами.
Метод работы с окнами связал умножение идеального импульсного ответа с функцией окна, чтобы сгенерировать соответствующий фильтр, который заостряется идеальный импульсный ответ. Как метод выборки частоты, метод работы с окнами производит фильтр, частотная характеристика которого аппроксимирует желаемую частотную характеристику. Метод работы с окнами, однако, имеет тенденцию приводить к лучшим результатам, чем метод выборки частоты.
Тулбокс обеспечивает две функции для проекта фильтра оконного, fwind1 и fwind2. fwind1 разрабатывает двумерный фильтр при помощи двумерного окна, которое он создает из одного или двух одномерных окон, которые вы задаете. fwind2 разрабатывает двумерный фильтр при помощи заданного двумерного окна непосредственно.
fwind1 поддерживает два различных метода для того, чтобы сделать двумерные окна, которые он использует:
Преобразование одного одномерного окна, чтобы создать двумерное окно, которое является почти циркулярное симметричный, при помощи процесса, подобного вращению
Создание прямоугольного, отделимого окна из двух одномерных окон, путем вычисления их векторного произведения
Пример ниже использует fwind1, чтобы создать 11 11 фильтр из желаемой частотной характеристики Hd. Пример использует функцию hamming Signal Processing Toolbox, чтобы создать одномерное окно, которое fwind1 затем расширяет к двумерному окну.
Hd = zeros(11,11); Hd(4:8,4:8) = 1; [f1,f2] = freqspace(11,'meshgrid'); mesh(f1,f2,Hd), axis([-1 1 -1 1 0 1.2]), colormap(jet(64)) h = fwind1(Hd,hamming(11)); figure, freqz2(h,[32 32]), axis([-1 1 -1 1 0 1.2])
Желаемая двумерная частотная характеристика (слева) и фактическая двумерная частотная характеристика (справа)
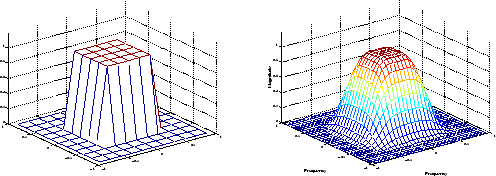
Функции проекта фильтра fsamp2, fwind1 и fwind2 все создают фильтры на основе желаемой матрицы значения частотной характеристики. Частотная характеристика является математической функцией, описывающей усиление фильтра в ответ на различные входные частоты.
Можно создать соответствующую желаемую матрицу частотной характеристики использование функции freqspace. freqspace возвращает правильные, равномерно расположенные с интервалами значения частоты для любого ответа размера. Если вы создаете желаемую матрицу частотной характеристики использование точек частоты кроме возвращенных freqspace, вы можете получить неожиданные результаты, такие как нелинейная фаза.
Например, чтобы создать круговую идеальную частотную характеристику низкой передачи с сокращением в 0,5, использовать
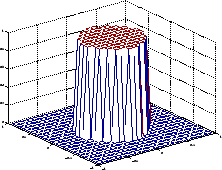
[f1,f2] = freqspace(25,'meshgrid'); Hd = zeros(25,25); d = sqrt(f1.^2 + f2.^2) < 0.5; Hd(d) = 1; mesh(f1,f2,Hd)
Идеальная круговая частотная характеристика низкой передачи
Обратите внимание на то, что для этой частотной характеристики, фильтры, произведенные fsamp2, fwind1 и fwind2, действительны. Этот результат желателен для большинства приложений для обработки изображений. Чтобы достигнуть этого в целом, желаемая частотная характеристика должна быть симметричной вокруг начала координат частоты (f1
=
0, f2
=
0).
Функция freqz2 вычисляет частотную характеристику для двумерного фильтра. Без выходных аргументов freqz2 создает сетчатый график частотной характеристики. Например, рассмотрите этот КИХ-фильтр,
h =[0.1667 0.6667 0.1667
0.6667 -3.3333 0.6667
0.1667 0.6667 0.1667];Эта команда вычисляет и отображается 64 64 частотная характеристика точки h.
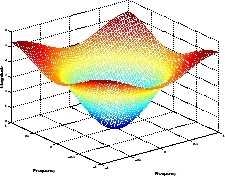
freqz2(h)
Частотная характеристика двумерного фильтра
Чтобы получить матрицу частотной характеристики H и векторы точки частоты f1 и f2, используйте выходные аргументы
[H,f1,f2] = freqz2(h);
freqz2 нормирует частоты f1 и f2 так, чтобы значение 1.0 соответствовало половине частоты дискретизации или π радианов.
Для простого m-by-n ответ, как показано выше, freqz2 использует двумерную функцию быстрого преобразования Фурье fft2. Можно также задать векторы произвольных точек частоты, но в этом случае freqz2 использует более медленный алгоритм.
Смотрите преобразование Фурье для получения дополнительной информации о быстром преобразовании Фурье и его приложении к линейной фильтрации и отфильтруйте проект.