Маленькие круги от центра, области значений и азимута
[lat,lon] = scircle1(lat0,lon0,rad)
[lat,lon] = scircle1(lat0,lon0,rad,az)
[lat,lon] = scircle1(lat0,lon0,rad,az,ellipsoid)
[lat,lon] = scircle1(lat0,lon0,rad,units)
[lat,lon] = scircle1(lat0,lon0,rad,az,units)
[lat,lon] = scircle1(lat0,lon0,rad,az,ellipsoid,units)
[lat,lon] = scircle1(lat0,lon0,rad,az,ellipsoid,units,npts)
[lat,lon] = scircle1(track,...)
[lat,lon] = scircle1(lat0,lon0,rad) вычисляет маленькие круги (на сфере) с центром в точке lat0,lon0 и радиус rad. Входные параметры могут быть скаляром или вектор-столбцами. Входной радиус имеет в градусах длину дуги на сфере.
[lat,lon] = scircle1(lat0,lon0,rad,az) использует вход az, чтобы задать маленькие круговые вычисленные дуги. Азимуты дуги измеряются по часовой стрелке от должного севера. Если az является вектор-столбцом, то длина дуги вычисляется с должного севера. Если az является матрицей 2D столбца, то маленькие круговые дуги вычисляются, начиная в азимуте в первом столбце и заканчиваясь в азимуте во втором столбце. Если az = [], то полный маленький круг вычисляется.
[lat,lon] = scircle1(lat0,lon0,rad,az,ellipsoid) вычисляет маленькие круги на эллипсоиде, заданном входом ellipsoid, а не путем принятия сферы. ellipsoid является referenceSphere, referenceEllipsoid, или объект oblateSpheroid или вектор формы [semimajor_axis eccentricity]. Если полуглавная ось является ненулевой, rad принят, чтобы быть в единицах расстояния, совпадающих с модулями полуглавной оси. Однако, если ellipsoid = [], или если полуглавная ось является нулем, то rad интерпретирован как угол и маленькие круги, вычисляется на сфере как в предыдущем синтаксисе.
[lat,lon] = scircle1(lat0,lon0,rad,units),
[lat,lon] = scircle1(lat0,lon0,rad,az,units), и
[lat,lon] = scircle1(lat0,lon0,rad,az,ellipsoid,units)
все допустимые формы вызова, которые используют входные модули, чтобы задать угловые модули вводов и выводов. Если вы не используете модули, 'degrees' принят.
[lat,lon] = scircle1(lat0,lon0,rad,az,ellipsoid, использует скалярный вход units,npts)npts, чтобы определить число точек на маленький вычисленный круг. Значение по умолчанию npts равняется 100.
[lat,lon] = scircle1(track,...) использование отслеживает, чтобы задать или большой радиус круговой или локсодромы. Если track = 'gc'track = 'rh', то круги с радиусами постоянного расстояния локсодромы вычисляются. Если вы не используете дорожку, 'gc' принят.
mat = scircle1(...) возвращает один выходной аргумент где mat = [lat lon]. Это полезно, если один маленький круг вычисляется.
Несколько кругов могут быть заданы от одной отправной точки путем обеспечения скалярных входных параметров lat0,lon0 и вектор-столбцов для rad и az при желании.
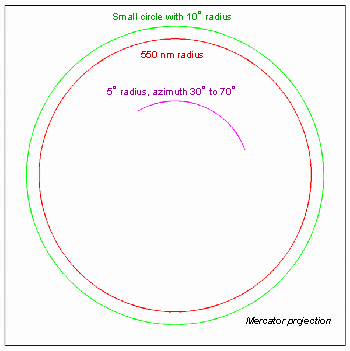
Создайте и постройте маленький круг, сосредоточенный в (0º, 0º) с радиусом 10º.
axesm('mercator','MapLatLimit',[-30 30],'MapLonLimit',[-30 30]);
[latc,longc] = scircle1(0,0,10);
plotm(latc,longc,'g')Если желаемый радиус известен в некоторой неугловой единице расстояния, используйте радиус, возвращенный функцией earthRadius как вход эллипсоида, чтобы установить модули области значений. (Используйте пустую запись азимута, чтобы указать на полный круг.)
[latc,longc] = scircle1(0,0,550,[],earthRadius('nm'));
plotm(latc,longc,'r')Для только дуги круга введите область значений азимута.
[latc,longc] = scircle1(0,0,5,[-30 70]); plotm(latc,longc,'m')