pdepe

Решите начальные краевые задачи для параболически-эллиптических УЧП в 1D

Синтаксис

sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan) sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options) [sol,tsol,sole,te,ie] = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options)

Аргументы

`m`	Параметр, соответствующий симметрии проблемы. `m` может быть плитой = `0`, цилиндрический = `1`, или сферический = `2`.
`pdefun`	Указатель на функцию, которая задает компоненты УЧП.
`icfun`	Указатель на функцию, которая задает начальные условия.
`bcfun`	Указатель на функцию, которая задает граничные условия.
`xmesh`	Вектор [`x0`, `x1`..., `xn`] определение точек, в которых числовое решение требуют для каждого значения в `tspan`. Элементы `xmesh` должны удовлетворить `x0 < x1 < ... < xn`. Длина `xmesh` должна быть > `= 3`.
`tspan`	Вектор [`t0`, `t1`..., `tf`] определение точек, в которых решение требуют для каждого значения в `xmesh`. Элементы `tspan` должны удовлетворить `t0 < t1 < ... < tf`. Длиной `tspan` должен быть `>=` `3`.
`options`	Некоторые опции базового решателя ОДУ доступны в `pdepe`: `RelTol`, `AbsTol`, `NormControl`, `InitialStep`, `MaxStep` и `Events`. В большинстве случаев значения по умолчанию для этих опций предоставляют удовлетворительные решения. Смотрите `odeset` для деталей.

Описание

sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan) решает начальные краевые задачи для систем параболических и эллиптических УЧП в одной пространственной переменной x и время t. pdefun, icfun и bcfun являются указателями на функцию. См. Создание указателя на функцию для получения дополнительной информации. Обыкновенные дифференциальные уравнения (ОДУ), следующие из дискретизации на пробеле, интегрированы, чтобы получить приближенные решения, время от времени задаваемые в tspan. Функция pdepe возвращает значения решения на mesh, обеспеченной в xmesh.

Параметризация Функций объясняет, как предоставить дополнительные параметры функциям pdefun, icfun или bcfun, при необходимости.

pdepe решает УЧП формы:

c (x, t, u, \frac{\partial u}{\partial x}) \frac{\partial u}{\partial t} = x^{- m} \frac{\partial}{\partial x} (x^{m} f (x, t, u, \frac{\partial u}{\partial x})) + s (x, t, u, \frac{\partial u}{\partial x})

(1)

УЧП содержат для t ₀ ≤ t ≤ _tf и a ≤ x ≤ b. Интервал [a, b] должен быть конечным. m может быть 0, 1, или 2, соответствуя плите, цилиндрической, или сферической симметрии, соответственно. Если m> 0, то a должен быть ≥ 0.

В уравнении 1, f (x, t, u, ∂u / ∂ x) является термином потока, и s (x, t, u, ∂u / ∂ x) является характеристиками выброса. Связь частных производных относительно времени ограничивается умножением диагональным матричным c (x, t, u, ∂u / ∂ x). Диагональные элементы этой матрицы являются или тождественно нулем или положительный. Элемент, который является тождественно нулевым, соответствует эллиптическому уравнению и в противном случае к параболическому уравнению. Должно быть по крайней мере одно параболическое уравнение. Элемент c, который соответствует параболическому уравнению, может исчезнуть в изолированных значениях x, если те значения x являются точками mesh. Разрывы в c и/или s из-за материальных интерфейсов разрешены при условии, что точка mesh помещается в каждый интерфейс.

Для t = t ₀ и весь x, компоненты решения удовлетворяют начальные условия формы

u (x, t_{0}) = u_{0} (x)

(2)

Для всего t и или x = a или x = b, компоненты решения удовлетворяют граничное условие формы

p (x, t, u) + q (x, t) f (x, t, u, \frac{\partial u}{\partial x}) = 0

(3)

Элементы q являются или тождественно нулем или никогда не обнуляют. Обратите внимание на то, что граничные условия выражаются с точки зрения потока f, а не ∂u / ∂ x. Кроме того, этих двух коэффициентов только p может зависеть от u.

В вызове sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan):

m соответствует m.
xmesh(1) и xmesh(end) соответствуют a и b.
tspan(1) и tspan(end) соответствуют t ₀ и _tf.
pdefun вычисляет условия c, f и s (уравнение 1). Это имеет форму
```
[c,f,s] = pdefun(x,t,u,dudx)
```
Входные параметры являются скалярами x и t и векторы u и dudx, которые аппроксимируют решение u и его частная производная относительно x, соответственно. c, f и s являются вектор-столбцами. c хранит диагональные элементы матричного c (уравнение 1).
icfun оценивает начальные условия. Это имеет форму
```
u = icfun(x)
```
Когда названо аргументом x, icfun оценивает и возвращает начальные значения компонентов решения в x в вектор-столбце u.
bcfun оценивает условия p и q граничных условий (уравнение 3). Это имеет форму
```
[pl,ql,pr,qr] = bcfun(xl,ul,xr,ur,t)
```
ul является приближенным решением на левом контуре xl =, a и ur являются приближенным решением на правильном контуре xr = b. pl и ql являются вектор-столбцами, соответствующими p и q, оцененному в xl, так же pr и qr соответствуют xr. Когда m> 0 и a = 0, ограниченность решения около x = 0 требует, чтобы поток f исчез в a = 0. pdepe налагает это граничное условие автоматически, и это игнорирует значения, возвращенные в pl и ql.

pdepe возвращает решение как многомерный массив sol. _ui = ui = sol (:, :, i) является приближением к i th компонент вектора решения u. Элемент ui (j, k) = sol (j, k, i) аппроксимирует _ui в (t, x) = (tspan (j), xmesh (k)).

ui = sol (j, :, i) аппроксимирует i компонента решения во время, которое tspan (j) и mesh указывает xmesh(:). Используйте pdeval, чтобы вычислить приближение и его частную производную ∂_ui / ∂ x в точках, не включенных в xmesh. Смотрите pdeval для деталей.

sol = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options) решает как выше с параметрами интегрирования по умолчанию, замененными значениями в options, аргумент, созданный с функцией odeset. Только некоторые опции базового решателя ОДУ доступны в pdepe: RelTol, AbsTol, NormControl, InitialStep и MaxStep. Значения по умолчанию, полученные, бросая входной параметр options, обычно будут удовлетворительными. Смотрите odeset для деталей.

[sol,tsol,sole,te,ie] = pdepe(m,pdefun,icfun,bcfun,xmesh,tspan,options) со свойством 'Events' в наборе options к указателю на функцию Events, решает как выше, также находя, где функции события g(t,u(x,t)) являются нулем. Для каждой функции вы задаете, должно ли интегрирование остановиться в нуле и имеет ли направление нулевого пересечения значение. Три вектор-столбца возвращены events: [value,isterminal,direction] = events(m,t,xmesh,umesh). xmesh содержит пространственную mesh, и umesh является решением в точках mesh. Используйте pdeval, чтобы оценить решение между точками mesh. Для функции события I-th value(i) является значением функции, ISTERMINAL(I) = 1, если интегрирование должно остановиться в нуле этой функции события и 0 в противном случае. direction(i) = 0, если все нули должны быть вычислены (значение по умолчанию), +1, если только нули, где функция события увеличивается, и-1, если только нули, где функция события уменьшается. Вывод tsol является вектор-столбцом времен, заданных в tspan до первого терминального события. SOL(j,:,:) является решением в T(j). TE является вектором времен, в которые события имеют место. SOLE(j,:,:) является решением в TE(j), и индексы в векторном IE задают, который имело место событие.

Если UI = SOL(j,:,i) аппроксимирует компонент i из решения во время, TSPAN(j) и mesh указывают XMESH, pdeval оценивает приближение и его частную производную ∂_ui / ∂ x в массиве точек XOUT и возвращает их в UOUT и DUOUTDX: [UOUT,DUOUTDX] = PDEVAL(M,XMESH,UI,XOUT)

Примечание

Частная производная ∂_ui / ∂ x оценена здесь, а не поток. Поток непрерывен, но в материале взаимодействуют через интерфейс, частная производная может иметь скачок.

Примеры

Пример 1. Этот пример иллюстрирует прямую формулировку, вычисление и графический вывод решения одного УЧП.

$π^{2} \frac{\partial u}{\partial t} = \frac{\partial}{\partial x} (\frac{\partial u}{\partial x})$

Это уравнение содержит через определенный интервал 0 ≤ x ≤ 1 в течение многих времен t ≥ 0.

УЧП удовлетворяет начальное условие

$u (x, 0) = \sin π x$

и граничные условия

$\begin{array}{l} u (0, t) \equiv 0 \\ π e^{- t} + \frac{\partial u}{\partial x} (1, t) = 0 \end{array}$

Удобно использовать локальные функции, чтобы поместить все функции, требуемые pdepe в одной функции.

function pdex11

m = 0;
x = linspace(0,1,20);
t = linspace(0,2,5);

sol = pdepe(m,@pdex1pde,@pdex1ic,@pdex1bc,x,t);
% Extract the first solution component as u.
u = sol(:,:,1);

% A surface plot is often a good way to study a solution.
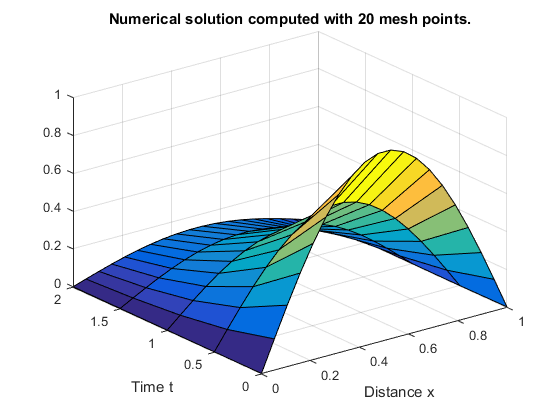
surf(x,t,u) 
title('Numerical solution computed with 20 mesh points.')
xlabel('Distance x')
ylabel('Time t')

% A solution profile can also be illuminating.
figure
plot(x,u(end,:))
title('Solution at t = 2')
xlabel('Distance x')
ylabel('u(x,2)')
% --------------------------------------------------------------
function [c,f,s] = pdex1pde(x,t,u,DuDx)
c = pi^2;
f = DuDx;
s = 0;
% --------------------------------------------------------------
function u0 = pdex1ic(x)
u0 = sin(pi*x);
% --------------------------------------------------------------
function [pl,ql,pr,qr] = pdex1bc(xl,ul,xr,ur,t)
pl = ul;
ql = 0;
pr = pi * exp(-t);
qr = 1;

В этом примере УЧП, начальное условие и граничные условия закодированы в локальных функциях pdex1pde, pdex1ic и pdex1bc.

Объемная поверхностная диаграмма показывает поведение решения.

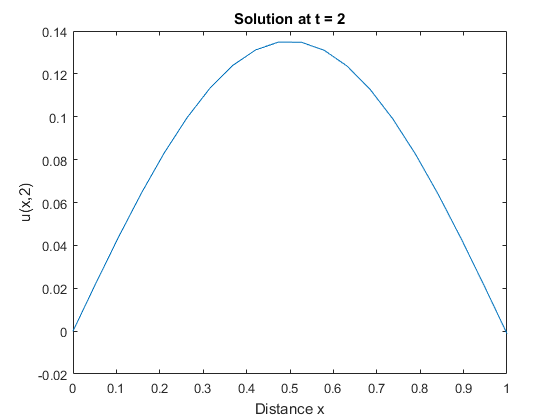
Следующий график показывает профиль решений в окончательном значении t (т.е. t = 2).

Пример 2. Этот пример иллюстрирует решение системы УЧП. Проблема имеет пограничные слои в обоих концах интервала. Решение изменяется быстро для маленького t.

УЧП

$\begin{matrix} \frac{\partial u_{1}}{\partial t} = 0.024 \frac{\partial^{2} u_{1}}{\partial x^{2}} - F (u_{1} - u_{2}) \\ \frac{\partial u_{2}}{\partial t} = 0.170 \frac{\partial^{2} u_{2}}{\partial x^{2}} + F (u_{1} - u_{2}) \end{matrix}$

где F (y) = exp (5.73y) – exp (–11.46y).

Это уравнение содержит через определенный интервал 0 ≤ x ≤ 1 в течение многих времен t ≥ 0.

УЧП удовлетворяет начальные условия

$\begin{matrix} u_{1} (x, 0) \equiv 1 \\ u_{2} (x, 0) \equiv 0 \end{matrix}$

и граничные условия

$\begin{array}{l} \frac{\partial u_{1}}{\partial x} (0, t) \equiv 0 \\ u_{2} (0, t) \equiv 0 \\ u_{1} (1, t) \equiv 1 \\ \frac{\partial u_{2}}{\partial x} (1, t) \equiv 0 \end{array}$

В форме, ожидаемой pdepe, уравнения

$[\begin{array}{l} 11 \end{array}] \cdot * \frac{\partial}{\partial t} [\begin{array}{l} u_{1} \\ u_{2} \end{array}] = \frac{\partial}{\partial x} [\begin{array}{l} 0.024 (\partial u_{} 1/ \partial x) \\ 0.170 (\partial u_{} 2/ \partial x) \end{array}] + [\begin{array}{r} - F (u_{1} - u_{2}) \\ F (u_{1} - u_{2}) \end{array}]$

Граничные условия на частных производных u должны быть записаны с точки зрения потока. В форме, ожидаемой pdepe, левое граничное условие

$[\begin{matrix} 0 \\ u_{2} \end{matrix}] + [\begin{array}{l} 10 \end{array}] \cdot * [\begin{array}{l} 0.024 (\partial u_{} 1/ \partial x) \\ 0.170 (\partial u_{} 2/ \partial x) \end{array}] = [\begin{array}{l} 00 \end{array}]$

и правильное граничное условие

$[\begin{matrix} u_{1} - \\ 10 \end{matrix}] + [\begin{array}{l} 01 \end{array}] \cdot * [\begin{array}{l} 0.024 (\partial u_{} 1/ \partial x) \\ 0.170 (\partial u_{} 2/ \partial x) \end{array}] = [\begin{array}{l} 00 \end{array}]$

Решение изменяется быстро для маленького t. Программа выбирает размер шага вовремя, чтобы разрешить это резкое изменение, но видеть это поведение в графиках, пример должен выбрать выходные времена соответственно. Существуют пограничные слои в решении в обоих концах [0,1], таким образом, точки mesh мест в качестве примера около 0 и 1, чтобы разрешить эти резкие изменения. Часто некоторое экспериментирование необходимо, чтобы выбрать mesh, которая показывает поведение решения.

function pdex4
m = 0;
x = [0 0.005 0.01 0.05 0.1 0.2 0.5 0.7 0.9 0.95 0.99 0.995 1];
t = [0 0.005 0.01 0.05 0.1 0.5 1 1.5 2];

sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);
u1 = sol(:,:,1);
u2 = sol(:,:,2);

figure
surf(x,t,u1)
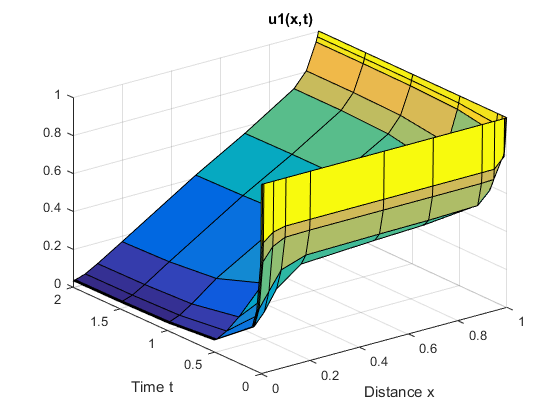
title('u1(x,t)')
xlabel('Distance x')
ylabel('Time t')

figure
surf(x,t,u2)
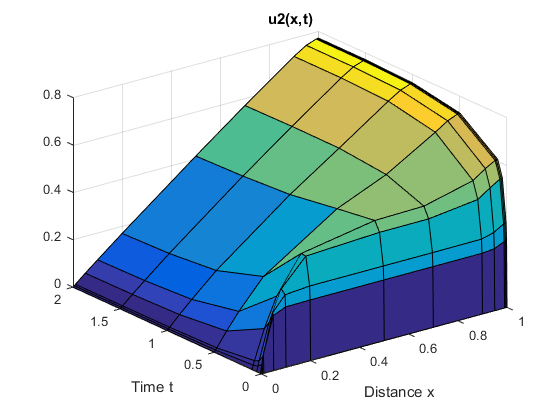
title('u2(x,t)')
xlabel('Distance x')
ylabel('Time t')
% --------------------------------------------------------------
function [c,f,s] = pdex4pde(x,t,u,DuDx)
c = [1; 1]; 
f = [0.024; 0.17] .* DuDx; 
y = u(1) - u(2);
F = exp(5.73*y)-exp(-11.47*y);
s = [-F; F]; 
% --------------------------------------------------------------
function u0 = pdex4ic(x);
u0 = [1; 0]; 
% --------------------------------------------------------------
function [pl,ql,pr,qr] = pdex4bc(xl,ul,xr,ur,t)
pl = [0; ul(2)]; 
ql = [1; 0]; 
pr = [ur(1)-1; 0]; 
qr = [0; 1];

В этом примере УЧП, начальные условия и граничные условия закодированы в локальных функциях pdex4pde, pdex4ic и pdex4bc.

Объемные поверхностные диаграммы показывают поведение компонентов решения.

Советы

Массивы xmesh и tspan играют различные роли в pdepe.
tspan Функция pdepe выполняет интеграцию времени с решателем ОДУ, который выбирает и временной шаг и формулу динамически. Элементы tspan просто задают, где вы хотите ответы, и стоимость зависит слабо от длины tspan.
xmesh – Приближения второго порядка к решению сделаны на mesh, заданной в xmesh. Обычно лучше использовать близко расположенные точки mesh, где решение изменяется быстро. pdepe не выбирает mesh в x автоматически. Необходимо обеспечить соответствующую фиксированную mesh в xmesh. Стоимость зависит строго от длины xmesh. Когда m> 0, не необходимо использовать мелкую сетку около x = 0, чтобы составлять координатную особенность.
Интегрирование времени сделано с ode15s. pdepe использует возможности ode15s для решения дифференциально-алгебраических уравнений, которые возникают, когда уравнение 1 содержит эллиптические уравнения, и для обработки Якобианов с заданным шаблоном разреженности.
После дискретизации эллиптические уравнения дают начало алгебраическим уравнениям. Если элементы вектора начальных условий, которые соответствуют эллиптическим уравнениям, не "сопоставимы" с дискретизацией, pdepe пытается настроить их прежде, чем начать интегрирование времени. Поэтому решение, возвращенное в течение начального времени, может иметь ошибку дискретизации, сопоставимую с этим в любое другое время. Если mesh прекрасна достаточно, pdepe может найти сопоставимые начальные условия близко к данным единицам. Если pdepe отображает сообщение, что он испытывает затруднения при нахождении сопоставимых начальных условий, попытайтесь совершенствовать mesh.
Никакая корректировка не необходима для элементов вектора начальных условий, которые соответствуют параболическим уравнениям.

Ссылки

[1] Skeel, R. D. и М. Берзиньш, "Метод для Пространственной Дискретизации Параболических уравнений в Одной Пространственной переменной", SIAM Journal на Научном и Статистическом Вычислении, Издании 11, 1990, pp.1-32.

Документация

pdepe

Синтаксис

Аргументы

Описание

Примечание

Примеры

Советы

Ссылки

Смотрите также

Темы

Представлено до R2006a

Документация MATLAB

Поддержка