Класс: TriRep
(Не рекомендуемый), Преобразовывают координаты точки от барицентрического до Декартова
baryToCart(TriRep) не рекомендуется. Используйте barycentricToCartesian(triangulation) вместо этого.
TriRep не рекомендуется. Использование триангуляции вместо этого.
XC = baryToCart(TR, SI, B)
XC = baryToCart(TR, SI, B) возвращает Декартовы координаты XC каждой точки в B, который представляет барицентрические координаты относительно его связанного симплексного SI.
TR | Представление триангуляции. |
SI | Вектор-столбец симплексных индексов, которые индексируют в матрицу триангуляции TR.Triangulation |
B | B является матрицей, которая представляет барицентрические координаты точек, чтобы преобразовать относительно симплекс SI. B имеет размер m-by-k, где m = length(SI), число точек, чтобы преобразовать, и k является количеством вершин на симплекс. |
XC | Матрица Декартовых координат конвертированных точек. XC имеет размер m-by-n, где n является размерностью пробела, где триангуляция находится. Таким образом, Декартовыми координатами точки B(j) относительно симплексного SI(j) является XC(j). |
Вычислите Триангуляцию Делоне набора точек.
x = [0 4 8 12 0 4 8 12]'; y = [0 0 0 0 8 8 8 8]'; dt = DelaunayTri(x,y)
Вычислите барицентрические координаты центров вписанной окружности.
cc = incenters(dt); tri = dt(:,:);
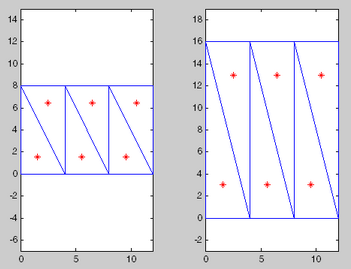
Постройте исходную триангуляцию и контрольные точки.
figure subplot(1,2,1); triplot(dt); hold on; plot(cc(:,1), cc(:,2), '*r'); hold off; axis equal;
Расширьте триангуляцию и вычислите сопоставленные местоположения центров вписанной окружности на деформированной триангуляции.
b = cartToBary(dt,[1:length(tri)]',cc); y = [0 0 0 0 16 16 16 16]'; tr = TriRep(tri,x,y) xc = baryToCart(tr, [1:length(tri)]', b);
Постройте деформированную триангуляцию и сопоставленные местоположения контрольных точек.
subplot(1,2,2); triplot(tr); hold on; plot(xc(:,1), xc(:,2), '*r'); hold off; axis equal;
cartesianToBarycentric | delaunayTriangulation | pointLocation | triangulation