Класс: TriRep
(Не рекомендуемый) Центры описанной окружности заданных симплекс
circumcenters(TriRep) не рекомендуется. Используйте circumcenter(triangulation) вместо этого.
TriRep не рекомендуется. Использование триангуляции вместо этого.
CC = circumcenters(TR, SI)
[CC RCC] = circumcenters(TR, SI)
CC = circumcenters(TR, SI) возвращает координаты центра описанной окружности каждого заданного симплексного SI. CC является m-by-n матрица, где m имеет длину length(SI), количество заданных симплекс, и n является размерностью пробела, где триангуляция находится.
[CC RCC] = circumcenters(TR, SI) возвращает центры описанной окружности и соответствующие радиусы ограниченных кругов или сфер.
TR | Объект Triangulation. |
SI | Вектор-столбец симплексных индексов, которые индексируют в матрицу триангуляции TR.Triangulation. Если SI не указан, информация центра описанной окружности для целой триангуляции возвращена, где центром описанной окружности, сопоставленным с симплексным i, является i 'th строка CC. |
CC | m-by-n матрица. m является количеством заданных симплекс, и n является размерностью пробела, где триангуляция находится. Каждая строка CC(i,:) представляет координаты центра описанной окружности симплексного SI(i). |
RCC | Вектор длины length(SI), количество заданных симплекс, содержащих радиусы ограниченных кругов или сфер. |
Загрузите 2D триангуляцию.
load trimesh2d trep = TriRep(tri, x,y)
Вычислите центры описанной окружности.
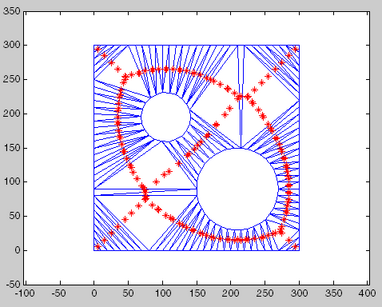
cc = circumcenters(trep); triplot(trep); axis([-50 350 -50 350]); axis equal; hold on; plot(cc(:,1),cc(:,2),'*r'); hold off;
Центры описанной окружности представляют точки на средней оси полигона.
Запросите 3-D триангуляцию, созданную с DelaunayTri. Вычислите центры описанной окружности первых пяти тетраэдров.
X = rand(10,3); dt = DelaunayTri(X); cc = circumcenters(dt, [1:5]')