Класс: TriRep
(Не рекомендуемый) Модульные нормали заданным треугольникам
faceNormals(TriRep) не рекомендуется. Используйте faceNormal(triangulation) вместо этого.
TriRep не рекомендуется. Использование триангуляции вместо этого.
FN = faceNormals(TR, TI)
FN = faceNormals(TR, TI) возвращает модульный вектор нормали в каждый заданный TI треугольников.
Этот запрос только применим к треугольным поверхностным сеткам.
TR | Представление триангуляции. |
TI | Вектор-столбец индексов, которые индексируют в матрицу триангуляции TR.Triangulation. |
FN |
Если TI не задан модуль, нормальная информация для целой триангуляции возвращена, где нормальное сопоставило с треугольником, i - |
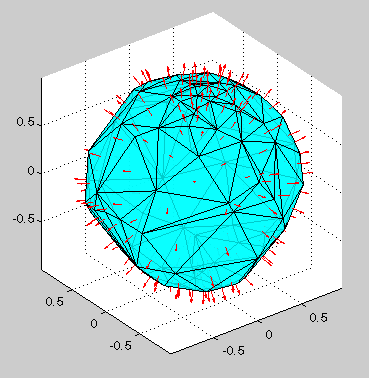
Триангулируйте выборку случайных точек на поверхности сферы и используйте TriRep, чтобы вычислить нормальное к каждому треугольнику:
numpts = 100;
thetha = rand(numpts,1)*2*pi;
phi = rand(numpts,1)*pi;
x = cos(thetha).*sin(phi);
y = sin(thetha).*sin(phi);
z = cos(phi);
dt = DelaunayTri(x,y,z);
[tri Xb] = freeBoundary(dt);
tr = TriRep(tri, Xb);
P = incenters(tr);
fn = faceNormals(tr);
trisurf(tri,Xb(:,1),Xb(:,2),Xb(:,3), ...
'FaceColor', 'cyan', 'faceAlpha', 0.8);
axis equal;
hold on;
Отобразите результат с помощью графика полей градиента:
quiver3(P(:,1),P(:,2),P(:,3), ...
fn(:,1),fn(:,2),fn(:,3),0.5, 'color','r');
hold off;