Класс: TriRep
(Не рекомендуемый), на Фасеты ссылается только один симплекс
freeBoundary(TriRep) не рекомендуется. Используйте freeBoundary(triangulation) вместо этого.
TriRep не рекомендуется. Использование триангуляции вместо этого.
FF = freeBoundary(TR)
[FF XF] = freeBoundary(TR)
FF = freeBoundary(TR) возвращает матричный FF, который представляет свободные граничные фасеты триангуляции. Фасет находится на свободном контуре, если на это ссылается только один симплекс (треугольник/четырехгранник, и т.д.). FF имеет размер m-by-n, где m является количеством граничных фасетов, и n является количеством вершин на фасет. Вершины индекса фасетов в массив точек, представляющих вершину, координируют TR.X. Массив FF мог быть пустым как в случае треугольной mesh, представляющей поверхность сферы.
[FF XF] = freeBoundary(TR) возвращает матрицу свободных граничных фасетов
TR | Представление триангуляции. |
FF |
FF, которому задали вершины с точки зрения компактного массива координат XF. |
XF | XF имеет размер m-by-ndim, где m является количеством свободных фасетов, и ndim является размерностью пробела, где триангуляция находится |
Используйте TriRep, чтобы вычислить граничную триангуляцию импортированной триангуляции.
Загрузите 3-D триангуляцию:
load tetmesh; trep = TriRep(tet, X);
Вычислите граничную триангуляцию:
[tri xf] = freeBoundary(trep);
Постройте граничную триангуляцию:
trisurf(tri, xf(:,1),xf(:,2),xf(:,3), ...
'FaceColor','cyan', 'FaceAlpha', 0.8);
Выполните прямой запрос 2D триангуляции, созданной с DelaunayTri.
Постройте mesh:
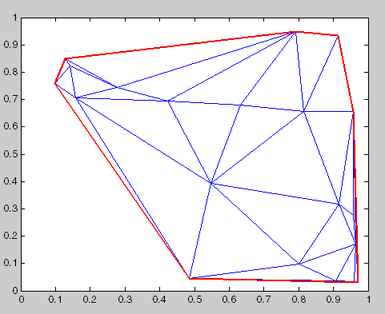
x = rand(20,1); y = rand(20,1); dt = DelaunayTri(x,y); fe = freeBoundary(dt)'; triplot(dt); hold on;
Отобразите свободные граничные ребра красного цвета:
plot(x(fe), y(fe), '-r', 'LineWidth',2) ; hold off;
В этом экземпляре свободные ребра соответствуют выпуклой оболочке (x, y).
convexHull | delaunayTriangulation | faceNormal | featureEdges | triangulation