Правильные углы фазы, чтобы произвести более сглаженные графики фазы
Q = unwrap(P)
Q = unwrap(P,tol)
Q = unwrap(P,[],dim)
Q = unwrap(P,tol,dim)
Q = unwrap(P) исправляет углы фазы радиана в векторном P путем добавления множителей ±2π, когда переходы в абсолютных адресах между последовательными элементами P больше, чем или равны допуску скачка по умолчанию π радианов. Если P является матрицей, unwrap действует по столбцам. Если P является многомерным массивом, unwrap работает с первой неодноэлементной размерностью.
Q = unwrap(P,tol) использует допуск скачка tol вместо значения по умолчанию, π.
Q = unwrap(P,[],dim) разворачивает вдоль dim с помощью допуска по умолчанию.
Q = unwrap(P,tol,dim) использует допуск скачка tol.
Допуск скачка меньше, чем π имеет тот же эффект как допуск π. Для допуска меньше, чем π, если бы скачок больше, чем допуск, но меньше, чем π, добавляя ±2π привели бы к скачку, больше, чем существующий, таким образом, unwrap выбирает текущую точку. Если вы хотите устранить скачки, которые являются меньше, чем π, пытаются использовать более прекрасную сетку в области.
Следующие данные о фазе прибывают из частотной характеристики передаточной функции третьего порядка. Кривая фазы переходит радианы 3.5873 между w = 3.0 и w = 3.5 от -1.8621 до 1.7252.
w = [0:.2:3,3.5:1:10];
p = [ 0
-1.5728
-1.5747
-1.5772
-1.5790
-1.5816
-1.5852
-1.5877
-1.5922
-1.5976
-1.6044
-1.6129
-1.6269
-1.6512
-1.6998
-1.8621
1.7252
1.6124
1.5930
1.5916
1.5708
1.5708
1.5708 ];
semilogx(w,p,'b*-'), hold 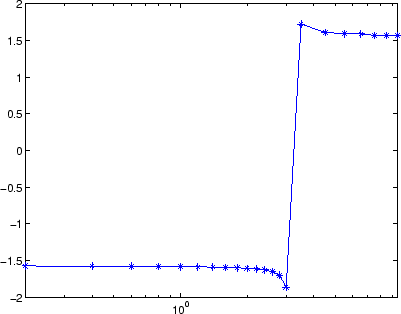
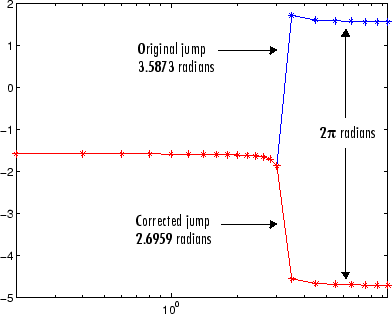
Используя unwrap, чтобы исправить угол фазы, получившимся скачком является 2.6959, который является меньше, чем допуск скачка по умолчанию π. Эта фигура строит новую кривую по исходной кривой.
semilogx(w,unwrap(p),'r*-')
Массив P показывает гладко увеличивающиеся углы фазы за исключением разрывов в элементах (3,1) и (1,2).
P = [ 0 7.0686 1.5708 2.3562
0.1963 0.9817 1.7671 2.5525
6.6759 1.1781 1.9635 2.7489
0.5890 1.3744 2.1598 2.9452 ]Функциональный Q = unwrap(P) устраняет эти разрывы.
Q =
0 7.0686 1.5708 2.3562
0.1963 7.2649 1.7671 2.5525
0.3927 7.4613 1.9635 2.7489
0.5890 7.6576 2.1598 2.9452