Когда вы рассматриваете результаты оптимизации суммы, раскладка по умолчанию отображает все результаты оптимизации и результаты для определенных решений.
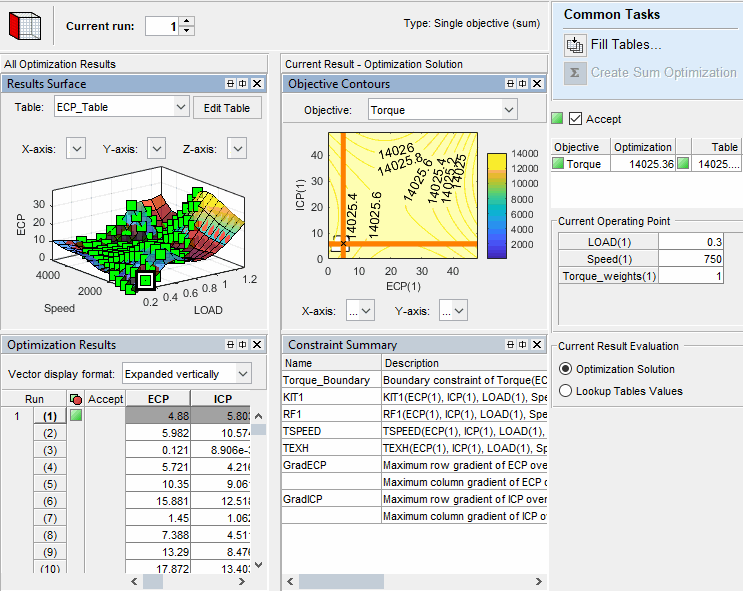
Левая сторона размещения показывает Поверхность Результатов и представления Результатов оптимизации для всех результатов. Если вы выбираете выполнение:
Объективные представления Сводных данных Контуров и Ограничения обеспечивают результаты оптимизации.
Текущая Операционная Панель показывает рабочую точку.
В любом представлении можно изменить представление путем щелчка правой кнопкой и выбора Current View, чтобы видеть опции представления.
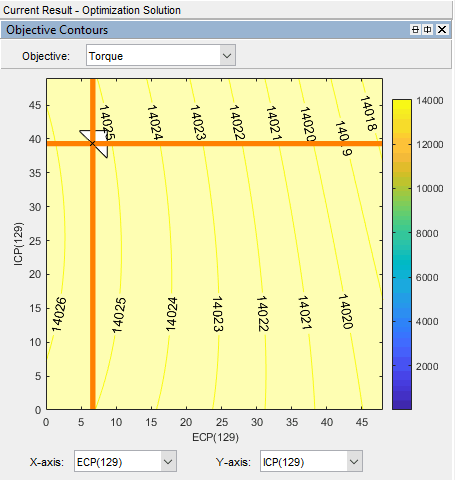
Объективный контурный график для проблем цели суммы показывает контуры цели. Можно отобразить графики против любой пары параметров управления в каждой точке в наборе рабочих точек в рамках каждого выполнения. В этой фигуре контурный график показывает результаты для запущенного 129.
Ограничительные сводные данные для оптимизации суммы показывают сводные данные всего ограничения выходные параметры для каждого ограничения при оптимизированных установках управляющих параметров для выбранного выполнения.

Строки таблицы show сводные данные в каждой рабочей точке. В этом случае каждая из строк соответствует оценке ограничения в каждой рабочей точке в рамках выполнения. Например, строки ограничений GradECP предоставляют оценке максимальные градиенты строки и столбца ECP по загрузке.
Функции таблицы Optimization Results маркированы в этой фигуре.
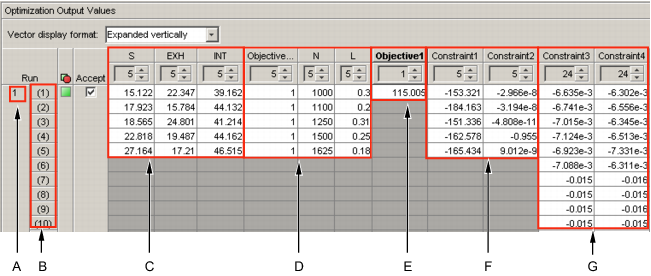
Ключ к таблице результатов оптимизации
A: Индекс выполнения — Индекс в набор рабочих точек, который отображается.
B: Индекс количества.
Для фиксированных и свободных переменных, соответствует индексу рабочей точки в рамках выполнения.
Для целей, соответствует индексу вывода для определенной маркированной цели.
Для ограничений, соответствует индексу вывода для определенного маркированного ограничения.
C: Оптимальные Настройки Свободной переменной — оптимальные настройки в этом случае S, EXH и INT в каждой рабочей точке в выполнении. Например, оптимальными настройками S, EXH и INT в третьей рабочей точке в этом выполнении 1 является S =18.565 °, EXH = 24,801 °, INT = 41,214 °
D: Настройки Фиксированной переменной — Настройки задают рабочие точки для выполнения и других фиксированных переменных (таких как веса) требуемый для целей и ограничений. Эти значения были настроены, прежде чем оптимизация была запущена.
E: Оптимальные объективные выходные параметры — Оптимальные значения любых объективных выходных параметров, то есть, оптимизированное значение взвешенной суммы TQ (115,002 нм) по этим пяти рабочим точкам, показанным в этом случае.
F, G: Ограничение выходные параметры при оптимизированных установках управляющих параметров — значение ограничения выходные параметры отображено здесь. Для проблемы в качестве примера образцовое ограничение, выводы отображены в разделе, маркировало F. Количество ограничения выходные параметры совпадает с количеством рабочих точек. Табличное ограничение градиента выводы отображены в разделе, маркировало G. Количество значений, возвращенных табличным ограничением градиента, зависит от внутренних настроек того ограничения.
Как в панели Значений Входной переменной в представлении Optimization, в выходном представлении, номер в скобке указывает на индекс рабочей точки в рамках выполнения.
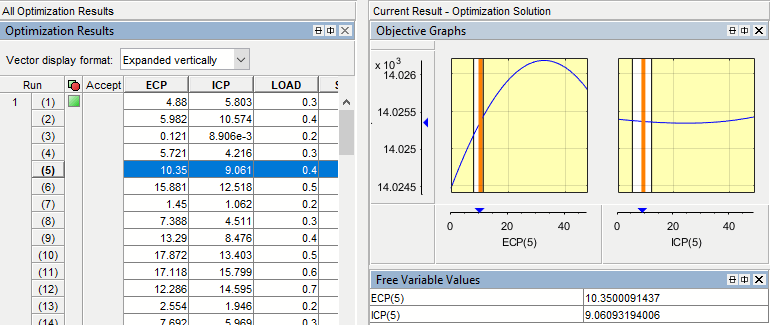
В таблице Optimization Results индекс рабочей точки в рамках выполнения показывают в скобках. В таблице Free Variable Values и графических дисплеях, InputVariableName(i) обеспечивает входную переменную в i-th рабочей точке в рамках выполнения. Например, ECP(5) является выхлопной фазой бегунка в 5-й рабочей точке, и ISP(5) является фазой бегунка потребления в первой рабочей точке.
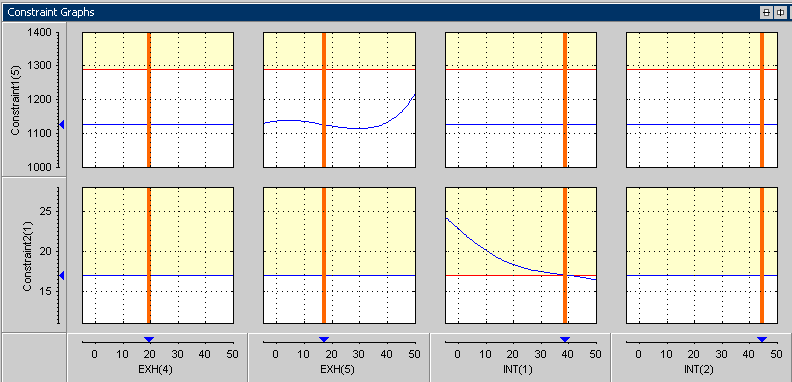
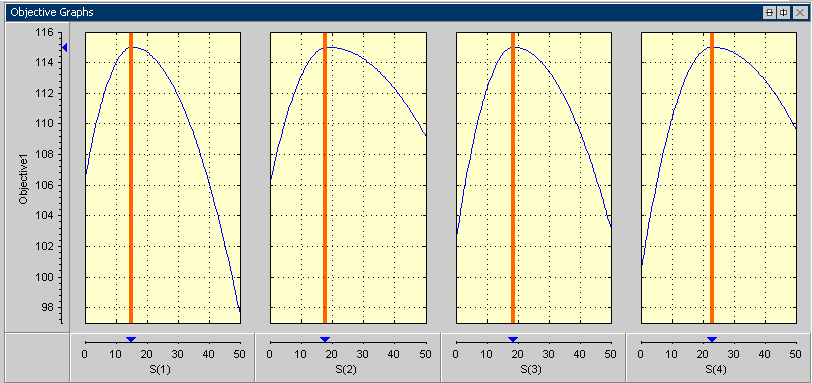
Объективные графики для проблем цели суммы показывают объективные графики сечения как в случае точки. Однако графики теперь отображены против каждого параметра управления в каждой точке в наборе рабочих точек в рамках каждого выполнения. В этой фигуре взвешенная сумма TQ построена против значений искры в первых четырех рабочих точках в запущенном 1.
Ограничительные графики для проблем цели суммы показывают графики сечения левой стороны ограничений как в случае точки. Однако в случае суммы существует еще несколько вводов и выводов, которые могут быть построены. А именно, каждое ограничение может возвратить несколько выходных параметров. Можно отобразить выводы против каждого параметра управления в каждой точке в наборе рабочих точек в рамках каждого выполнения.