CAGE может решить оптимизацию типа суммы. Эта оптимизация находит оптимальные настройки параметров управления в нескольких рабочих точках одновременно. Можно использовать оптимизацию суммы, чтобы решить проблемы цикла диска, где необходимо применить ограничения через целый цикл. Например, ограничение, такое как взвешенный механизм тормозит определенный NOx <= 3 г/кВт·ч.
Если у вас есть существующая оптимизация точки, можно использовать утилиту, чтобы создать оптимизацию суммы из оптимизации точки вывод. Этот подход может помочь вам найти хорошие начальные значения для оптимизации суммы. Создать оптимизацию суммы из вашей оптимизации точки:
(Рекомендуемый) Выбирают Solution> Create Sum Optimization . Для получения дополнительной информации смотрите, Создают Оптимизацию Суммы из Оптимизации Точки Вывод.
Выберите Optimization> Convert to Sum Optimization .
Если у вас нет существующей оптимизации точки, чтобы настроить новую оптимизацию суммы:
Используйте Оптимизацию Создания от Мастера Моделей, чтобы создать вашу оптимизацию. Можно сконфигурировать цель суммы в мастере. CAGE автоматически конфигурирует ваши значения переменных правильно для оптимизации суммы, задавая одно выполнение. Смотрите то, Что Выполнение?.
Можно также сконфигурировать цель суммы позже в представлении Optimization. Смотрите Цели Суммы.
Добавьте ограничения:
Можно добавить граничное образцовое ограничение в мастере.
Чтобы применить другие типы ограничений, необходимо использовать представление Optimization. Можно применяться линейный, эллипсоид, 1D таблица, 2D таблица и ограничения области значений, и некоторые ограничения конкретны, чтобы суммировать оптимизацию — ограничения суммы и табличные ограничения градиента.
Смотрите Ограничение Редактирования для деталей всех этих ограничений.
Выберите точки, где вы хотите запустить оптимизацию:
Можно использовать мастер, чтобы выбрать подходящую табличную сетку, набор данных или детальную модель, или использовать переменные сетболы.
Можно также настроить значения переменных оптимизации в представлении Optimization. Можно ввести значения вручную, или путем импорта из наборов данных, таблиц или вывода существующей оптимизации. Смотрите Значения переменных Редактирования.
Для оптимизации суммы у вас должно быть одно выполнение, заданное средствами управления длиной. CAGE автоматически конфигурирует ваши значения переменных правильно для оптимизации суммы (задающий одно выполнение) когда вы также:
Используйте утилиту Create Sum Optimization
Используйте мастер Create Optimization from Model и затем выберите цель суммы.
Если вы предпочитаете, можно использовать средства управления длиной в представлении Optimization вместо мастера. Смотрите Выбирающие Скалярные Переменные.
(Необязательно) можно оценить цели или ограничения по различным рабочим точкам тем, вы задали в оптимизации. Смотрите Используя Наборы Точки Приложения.
Запустите оптимизацию. Смотрите Оптимизацию Выполнения.
Просмотрите результаты (см. Просмотр Ваших Результатов оптимизации). Для описаний оптимизации вывод, конкретный, чтобы суммировать проблемы, смотрите Оптимизацию Суммы Интерпретации Вывод.
Оптимизация типа суммы определяет оптимальные настройки рабочих точек одновременно. Таким образом один вызов алгоритма определяет оптимальные настройки параметров управления в каждой рабочей точке.
В CAGE run относится к каждому вызову алгоритма оптимизации.. Вы задаете количество выполнений, которые вы хотите, чтобы CAGE выполнил с управлением Number of runs в панели Input Variable Values. Для получения дополнительной информации смотрите Scalar Variables Выбора.
Следующие разделы описывают средства управления и выходные параметры для оптимизации суммы с помощью следующей проблемы в качестве примера для рисунка.
Скажите, что вы создали модели для крутящего момента (TQ), остаточная часть (RESIDFRAC) и исчерпываете температуру (EXTEMP) для бензинового двигателя.
Входные параметры к этим моделям
Усовершенствование Spark, S
Впустите синхронизацию бегунка, INT
Выхлопная синхронизация бегунка, EXH
Скорость вращения двигателя, N
Относительная загрузка, L
Необходимо настроить оптимизацию, чтобы вычислить оптимальные настройки S, INT и EXH для следующих рабочих точек:
| N | L |
|---|---|
| 1000 | 0.3 |
| 1100 | 0.2 |
| 1250 | 0.31 |
| 1500 | 0.25 |
| 1625 | 0.18 |
Цель для этой оптимизации:
Максимизируйте взвешенную сумму TQ по рабочим точкам.
Ограничения для этой оптимизации:
Ограничение 1: EXTEMP <= 1290°C в каждой рабочей точке
Ограничение 2: RESIDFRAC <= 17% в каждой рабочей точке
Ограничение 3: Изменение в INT - не больше, чем 5,5 ° на изменение на 500 об/мин в N и 5,5 ° на 0,1 изменения в L, оцененном по 3х3 (N, L) таблица.
Ограничение 4: Изменение в EXH - не больше, чем 5,5 ° на изменение на 500 об/мин в N и 5,5 ° на 0,1 изменения в L, оцененном по 3х3 (N, L) таблица.
Можно использовать алгоритм fmincon в CAGE, чтобы решить эту проблему.
Этот пример используется, чтобы объяснить средства управления и выходные параметры в следующих разделах, Выбор Scalar Variables и Interpreting Sum Optimization Output.
Смотрите Ограничения Алгоритма для получения дополнительной информации об ограничениях алгоритма оптимизации в CAGE.
В узле оптимизации панель Optimization Point Set перечисляет свободные и фиксированные переменные. Для оптимизации суммы:
Number of operating points является числом точек, которое оптимизатор суммирует во время оптимизации.
Используйте Select Scalar Variables, чтобы задать скалярные значения, которые не зависят от рабочих точек.
Каждое выполнение Оптимизации CAGE звонит алгоритму, который вы приняли решение использовать. Этот алгоритм должен оценить цели и ограничения (вероятно, несколько раз), чтобы позволить ему определять оптимальные настройки свободных переменных. Алгоритмы оптимизации обычно имеют ограничения на количество цели и ограничения выходные параметры, которые они могут обработать. Следующая таблица детализирует ограничения на эти два алгоритма, предоставленные в CAGE.
| Имя алгоритма | Цели | Ограничения |
|---|---|---|
| fmincon | Один вывод | Любое количество выходных параметров |
| NBI | Два или больше выходных параметров | Любое количество выходных параметров |
Когда каждая цель и ограничение оценены во время выполнения, количество выходных параметров, которые это возвращает, зависит от максимального количества значений всех его входных параметров. Следующая таблица детализирует количество выходных параметров, которые каждый объективный тип возвращает как функция максимального количества значений всех его входных параметров.
| Объективный тип | Максимальное количество значений всех входных параметров к цели | Количество Выходных параметров | Причина |
|---|---|---|---|
| Точка | N | N | Цель точки оценена в каждой рабочей точке в рамках выполнения, и все значения возвращены. |
| Сумма | N | Один | Цель суммы оценивает модель в каждой рабочей точке и возвращает одно значение, которое является взвешенной суммой образцовых оценок. |
Точно так же следующая таблица детализирует количество выходных параметров, которые каждый тип ограничения возвращает как функция максимального количества значений всех его входных параметров.
| Тип ограничения | Максимальное количество значений всех входных параметров к ограничению | Количество Выходных параметров | Причина |
|---|---|---|---|
| Линейный | N | N | Эти ограничения оценены в каждой рабочей точке в рамках выполнения, и все значения возвращены. |
| Эллипсоид | N | N | |
| 1D Таблица | N | N | |
| 2D Таблица | N | N | |
| Модель | N | N | |
| Область значений | N | 0, N или 2 Н | Ограничение области значений выполняет выражение в каждой рабочей точке в рамках выполнения. Ограничение возвращает два значения для каждой точки, расстояния от нижней и верхней границы. В этом случае 2 Н выводят, возвращены. Если одна из границ бесконечна, то только расстояние до связанного конечного возвращено для каждой точки и N, выходные параметры возвращены. Если обе границы будут бесконечны затем будут возвращены, то 0 выходных параметров. |
| Сумма | N | 1 | Ограничение суммы оценивает модель в каждой рабочей точке и возвращает различие между взвешенной суммой модели и связанным. |
| Таблица | N | > =8 (зависящий от настроек) | Табличное ограничение градиента ограничивает градиент свободной переменной по сетке. Количество возвращенных выходных параметров зависит от размерностей сетки. |
Можно использовать эти три таблицы, чтобы проверять, удовлетворяет ли настроенная проблема ограничения алгоритма. Как пример, следующая таблица проверяет, удовлетворяет ли проблема в качестве примера (подробный в проблеме В качестве примера Продемонстрировать Средства управления для Оптимизации Суммы) ограничение алгоритма, выбранного, чтобы решить его, fmincon.
| Цель | Максимальное количество значений всех входных параметров | Количество Выходных параметров |
|---|---|---|
| Взвешенная сумма TQ по точкам цикла диска | 5 | 1 (использование таблицы Objective) |
| Ограничение | Максимальное количество значений всех входных параметров | Количество Выходных параметров |
|---|---|---|
| EXTEMP <= 1290°C в каждой точке цикла диска | 5 | 5 (использование таблицы Constraint) |
| RESIDFRAC <= 17% в каждой точке цикла диска | 5 | 5 (использование таблицы Constraint) |
| Изменение в INT - не больше, чем 5,5 ° на 500 об/мин и 5,5 ° на 0,1 изменения в L | 5 | 24 (это значение является количеством табличного ограничения градиента выходные параметры, сгенерированные из 3х3 таблицы), |
| Изменение в EXH - не больше, чем 5,5 ° на 500 об/мин и 5,5 ° на 0,1 изменения в L | 5 | 24 (это значение является количеством табличного ограничения градиента выходные параметры, сгенерированные из 3х3 таблицы), |
Таким образом проблема в качестве примера имеет 1 объективный вывод и 58 ограничений выходные параметры. Это удовлетворяет ограничения алгоритма fmincon и таким образом, алгоритм может использоваться.
Можно использовать application point sets, чтобы оценить ограничения и цели в различных рабочих точках, чем заданные в оптимизации. Можно только использовать наборы точки приложения с оптимизацией суммы.
Это может быть полезно для некоторых проблем, например:
Ваша калибровочная проблема требует фактора нескольких циклов диска, заданных в различных наборах рабочей точки. Например, распространено иметь различные циклы диска для производительности и эмиссии.
Вы хотите применить некоторые ограничения только в подмножестве точек оптимизации (иногда называемый “проблемы мультиобласти”). Например, часто существуют различные ограничения, чтобы рассмотреть в предельной нагрузке.
Ваш полный набор рабочей точки интереса является очень большим и оптимизирует в каждой точке, будет очень медленным. Можно запустить оптимизацию в подмножестве точек и оценить интерполированные результаты через набор точки приложения.
Вы, возможно, должны оценить детальные модели в различных рабочих точках к точкам, где модели заданы.
Использовать набор точки приложения для оценки цели или ограничения:
Щелкните правой кнопкой по цели или ограничению, и выберите Select Application Point Set.
Диалоговое окно Select Operating Point Variables появляется.
Выберите пару переменных, чтобы использовать в наборах точки приложения. Переменные должны быть фиксированными переменными в вашей оптимизации. Вы только выбираете переменные однажды на оптимизацию. Нажмите OK.
Диалоговое окно Select Application Point Set появляется.
Выберите набор точки приложения. Можно выбрать набор данных или New subset точек оптимизации. Чтобы выбрать подмножество точек, можно использовать флажки или кликнуть по точкам на графике.
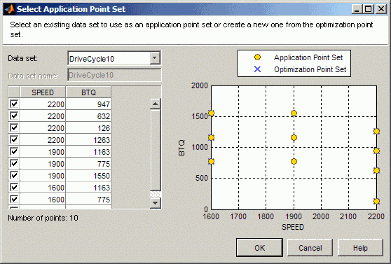
Просмотрите график, отображающий точки приложения и точки оптимизации. CAGE экстраполирует результаты оптимизации, чтобы оценить цель или ограничение в точках приложения.
Нажмите OK.
Чтобы видеть графики в качестве примера, которые иллюстрируют, как CAGE использует наборы точки приложения, введите mbcAppPointSetDemo, чтобы загрузить файл проекта в качестве примера mbcAppPointSetDemo.cag в CAGE. Запустите оптимизацию в проекте просмотреть графики.